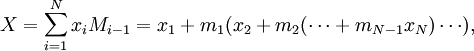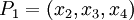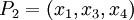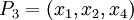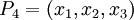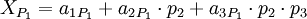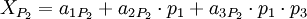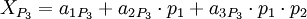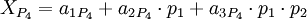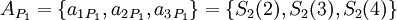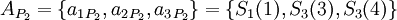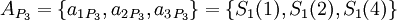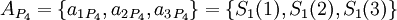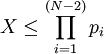Полиадический код — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 9: | Строка 9: | ||
| − | Любое число <math>\{ | + | Любое число <math>\{x_1,x_2,x_3,\ldots,x_n\}</math> в системе остаточных классов может быть представлено в виде полиадического кода |
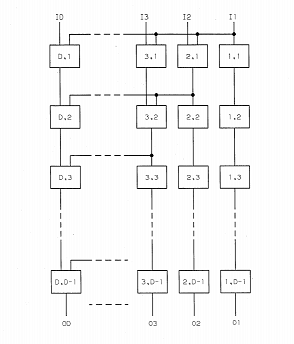
:<math>X=\sum_{i=1}^Nx_iM_{i-1}=x_1+m_1(x_2+m_2(\cdots+m_{N-1}x_{N})\cdots),</math> | :<math>X=\sum_{i=1}^Nx_iM_{i-1}=x_1+m_1(x_2+m_2(\cdots+m_{N-1}x_{N})\cdots),</math> | ||
| − | где <math>x_k</math> - цифры | + | где <math>x_k</math> - цифры кода, числа <math>M_k</math> - основание смешанной системы счисления: |
:<math>M_0=1,M_i=\prod_{j=1}^i m_j</math> для <math>i>0</math> и <math>0\leq x_i<m_i.</math> | :<math>M_0=1,M_i=\prod_{j=1}^i m_j</math> для <math>i>0</math> и <math>0\leq x_i<m_i.</math> | ||
Текущая версия на 09:24, 12 февраля 2015
Содержание
Введение
Полиадический код (или система счисления со смешанным основанием от англ. associated mixed radix system (AMRS))
Основанием смешанной системы счисления является возрастающая последовательность чисел 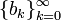 , и каждое число
, и каждое число 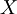 в ней представляется как линейная комбинация:
в ней представляется как линейная комбинация:
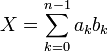 , где на коэффициенты
, где на коэффициенты 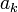 , называемые как и прежде цифрами, накладываются некоторые ограничения.
Записью числа
, называемые как и прежде цифрами, накладываются некоторые ограничения.
Записью числа  в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса
в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса 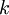 , начиная с первого ненулевого.
, начиная с первого ненулевого.
Любое число 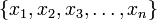 в системе остаточных классов может быть представлено в виде полиадического кода
в системе остаточных классов может быть представлено в виде полиадического кода
где 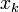 - цифры кода, числа
- цифры кода, числа 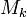 - основание смешанной системы счисления:
- основание смешанной системы счисления:
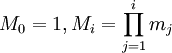 для
для 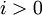 и
и 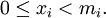
Полиадический код используется для:
- Сравнения чисел
- Перевода чисел из системы остаточных классов в обычную позиционную систему счисления
Обратное преобразование
Обратное преобразование на базе полиадического кода, базируется на идее, что любое число X может быть представлено в системе взаимно простых чисел 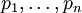 , как [1]:
, как [1]:
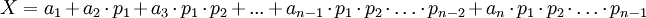 , где
, где 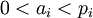
-
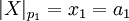
-
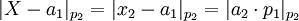 =>
=> 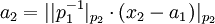
-
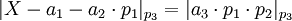 =>
=> 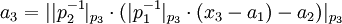
-
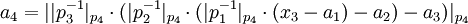
- ...
-
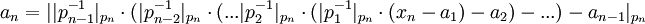
Для использования этого метода требуются константы вида 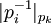 . Можно также заметить, что начинать вычисление
. Можно также заметить, что начинать вычисление 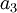 можно, как только появилось значение
можно, как только появилось значение 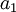 . На основе этого метода можно строить конвейерные преобразователи.
. На основе этого метода можно строить конвейерные преобразователи.
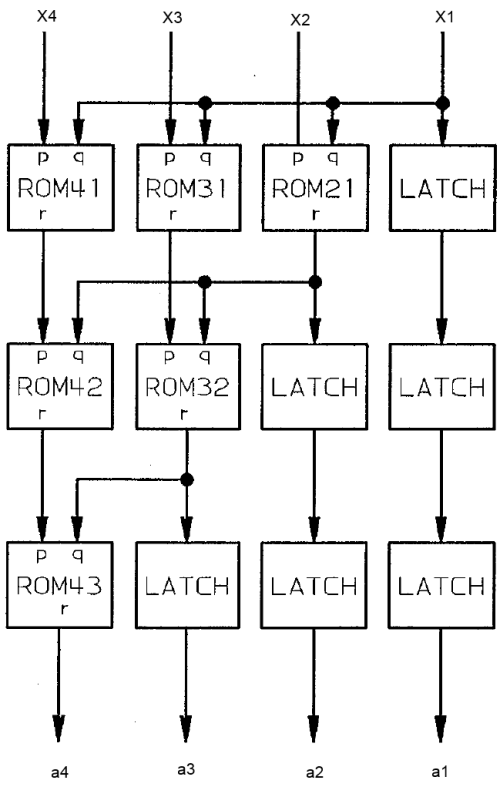
Конвейерный преобразователь в полиадический код
Используя формулы выше можно нарисовать схему конвейерного преобразователя. В данном случае мы используем модулярный базис из 4 элементов:
- ROMij - это таблица выполняющая следующее преобразование
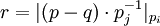 . Для больших значений модулей таблица может быть заменена на последовательный набор арифметических операций (вычитание, умножение на константу и взятие модуля)
. Для больших значений модулей таблица может быть заменена на последовательный набор арифметических операций (вычитание, умножение на константу и взятие модуля)
- LATCH - элемент памяти сохраняющий значение до следующего такта
- На преобразование модулярного представления в полиадический код требуется N-1 ступеней конвейера.
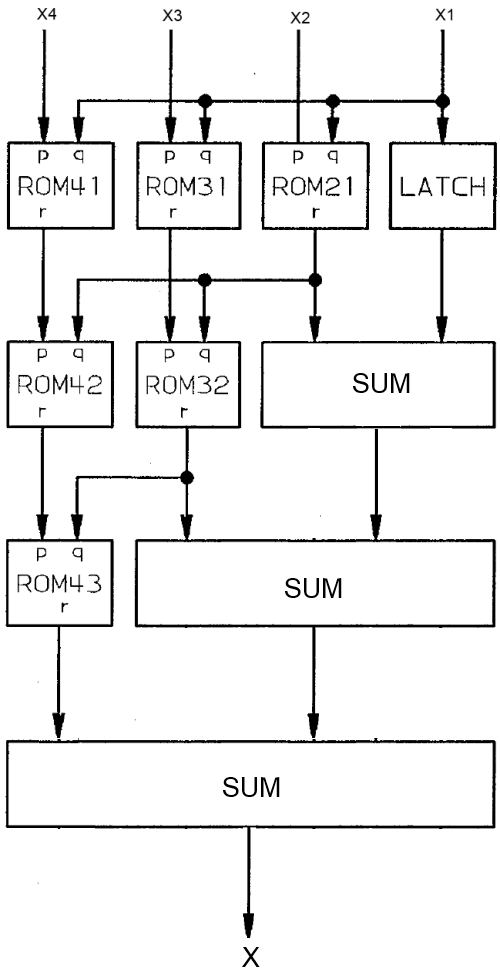
Обратный конвейерный преобразователь на базе полиадического кода
Этот преобразователь используется для восстановления числа 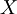 из модулярного кода, заданного набором остатков
из модулярного кода, заданного набором остатков 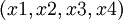 .
.
- ROMij - это таблица выполняющая следующее преобразование
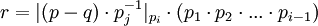 . Для больших значений модулей таблица может быть заменена на последовательный набор арифметических операций (вычитание, умножение на константу и взятие модуля)
. Для больших значений модулей таблица может быть заменена на последовательный набор арифметических операций (вычитание, умножение на константу и взятие модуля)
- LATCH - элемент памяти сохраняющий значение до следующего такта
- SUM - обычный сумматор
- На преобразование модулярного представления в позиционный вид требуется N ступеней конвейера.
- В отличие от преобразования в полиадический код, данный преобразователь получается более громоздким из-за более сложной структуры ROMij и наличия сумматоров, битовый размер которых растет в нижней части конвейера.
Коррекция ошибок на базе полиадического кода
Пусть задан набор модулей 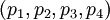 , где
, где 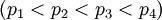 . Из них первые два
. Из них первые два 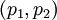 являются информационными, а последние два
являются информационными, а последние два 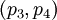 - проверочными. Данный набор позволяет корректировать одиночную ошибку в одном из модулярных каналов. Для коррекции можно использовать следующий наиболее простой подход на базе так называемой "репликации": из модулярного представления числа
- проверочными. Данный набор позволяет корректировать одиночную ошибку в одном из модулярных каналов. Для коррекции можно использовать следующий наиболее простой подход на базе так называемой "репликации": из модулярного представления числа 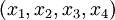 последовательно исключается каждый канал, формируя "исключающие наборы":
последовательно исключается каждый канал, формируя "исключающие наборы":
Динамический диапазон каждой из троек превышает заданный (можно убедиться для каждой тройки: 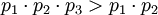 ). В случае если ошибок не было, то при обратном преобразовании в позиционное представление значения всех троек должны лежать в диапазоне:
). В случае если ошибок не было, то при обратном преобразовании в позиционное представление значения всех троек должны лежать в диапазоне: ![[0 <= X < p_1 \cdot p_2]](/w/images/math/7/5/6/756279094b6aca9ba967803c6f3bd159.png) и быть равными. В случае, если в одном из каналов произошла ошибка, то правильное значение даст только одна тройка, в которой исключено неверное значение, все остальные тройки будут лежать вне динамического диапазона (здесь нужна ссылка на пруФФФФФ или сам пруф).
и быть равными. В случае, если в одном из каналов произошла ошибка, то правильное значение даст только одна тройка, в которой исключено неверное значение, все остальные тройки будут лежать вне динамического диапазона (здесь нужна ссылка на пруФФФФФ или сам пруф).
В этом случае для восстановления числа требуется сделать 4 обратных преобразователя для каждой из троек. Сравнить полученные значения с 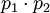 и на основании сравнения выдать на выход правильное значение. Однако, как будет показано ниже, корректирующий преобразователь можно значительно сократить по площади, объединив одинаковые части в каждом из обратных преобразователей и рассчитывая финальное позиционное значение только один раз для тройки с правильным значением.
и на основании сравнения выдать на выход правильное значение. Однако, как будет показано ниже, корректирующий преобразователь можно значительно сократить по площади, объединив одинаковые части в каждом из обратных преобразователей и рассчитывая финальное позиционное значение только один раз для тройки с правильным значением.
Запишем, полиадическую формулу для каждой из троек:
Если посмотреть на самую правое слагаемое каждого из выражений, можно заметить, что если любой из коэффициентов 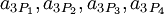 отличается от нуля, то всё выражение получается больше, чем
отличается от нуля, то всё выражение получается больше, чем 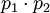 . Из чего следует, что выражение ошибочно. Этот факт можно использовать для определения ошибки, не восстанавливая значение целиком (нужен пруф). Тем самым можно сократить площадь преобразователя.
. Из чего следует, что выражение ошибочно. Этот факт можно использовать для определения ошибки, не восстанавливая значение целиком (нужен пруф). Тем самым можно сократить площадь преобразователя.
Схема сокращенного преобразователя в полиадический код для коррекции одиночной ошибки
Использовать несколько параллельных преобразователей оказывается неэффективным. Как показано в [2], для этой цели можно использовать сокращенную форму (см. рисунок ниже).
В этом случае на выходных узлах можно получить полиадическое представление для каждого из исключающих наборов 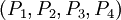 :
:
Для последующего восстановления исходного числа с коррекцией возможной ошибки можно воспользоваться следующим алгоритмом:
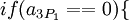
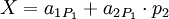
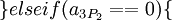
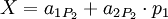
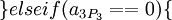
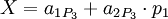
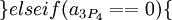
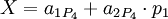
Ошибка более чем в 1 канале
Для произвольного значения 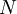 схема сокращенного преобразователя в полиадический код строится следующим образом.
Возьмем систему остатков для следующего набора
схема сокращенного преобразователя в полиадический код строится следующим образом.
Возьмем систему остатков для следующего набора 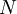 взаимно простых целых модулей:
взаимно простых целых модулей: 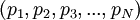 , где
, где 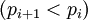 .
.
Пусть 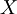 - целое число, такое, что
- целое число, такое, что
Представление числа 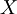 в модулярном виде
в модулярном виде 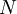 набором остатков таково:
набором остатков таково: 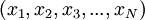 , где
, где 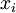 - значение остатка
- значение остатка 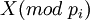 . В этом случае 2 цифры остатков избыточны. Данный набор позволяет найти и исправить одиночную ошибку в одном из модулярных каналов.
. В этом случае 2 цифры остатков избыточны. Данный набор позволяет найти и исправить одиночную ошибку в одном из модулярных каналов.
Для поиска и коррекции ошибок используется преобразование модулярного представления числа в полиадический код.
По набору 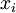 создается полиадический код - набор
создается полиадический код - набор 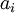 . Ошибочные каналы модулярного представления определяются следующим образом.
. Ошибочные каналы модулярного представления определяются следующим образом.
Во-первых, из 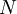 каналов модулярного представления числа
каналов модулярного представления числа 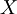 , создаем
, создаем 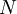 наборов по
наборов по 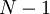 каналов, причем последовательно исключается каждый канал, формируя так называемые проекции ("исключающие наборы"). Пусть
каналов, причем последовательно исключается каждый канал, формируя так называемые проекции ("исключающие наборы"). Пусть 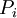 - проекция, полученная исключением канала
- проекция, полученная исключением канала 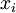 . Преобразуем в полиадический код каждую из проекций
. Преобразуем в полиадический код каждую из проекций 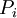 . Если для всех проекций старшие разряды полученного полиадического кода равны нулю, ни в одном канале
. Если для всех проекций старшие разряды полученного полиадического кода равны нулю, ни в одном канале 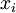 ошибки нет. Если полученные старшие разряды ненулевые для всех проекций, кроме
ошибки нет. Если полученные старшие разряды ненулевые для всех проекций, кроме 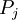 , то в канале
, то в канале 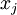 присутствует ошибка, а
присутствует ошибка, а 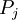 - правильное представление числа
- правильное представление числа 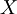 .
.
Пусть ROMij - это любая схема или программа, получающая в момент времени 0 на вход целые  и
и 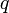 и в момент времени
и в момент времени 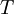 выдающая на выход
выдающая на выход  , где
, где 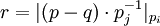 .
.
Пусть LATCH - это любая схема или программа, получающая в момент времени 0 на вход целое число и выдающая это число на выход в момент времени 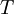 .
.
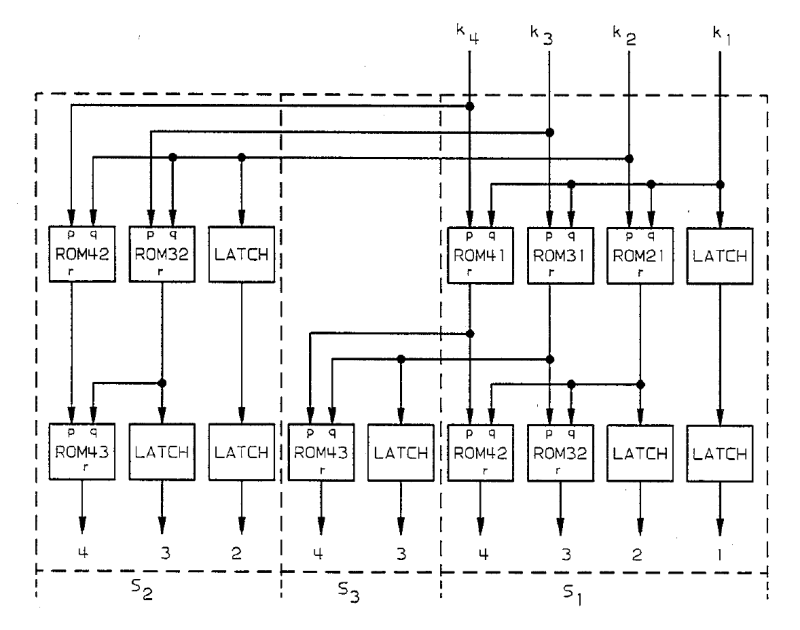
Можно получить конвейерную схему, реализующую преобразование в полиадический код, разместив и соединив элементы ROMij и LATCH, определенные выше, как показано на следующем рисунке.
Назовем эту схему схемой преобразователя в полиадический код размера 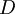 . На вход схемы поступают цифры остатков, обозначенные от
. На вход схемы поступают цифры остатков, обозначенные от 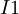 до
до 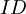 , а выходами являются цифры полиадического кода, обозначенные от
, а выходами являются цифры полиадического кода, обозначенные от 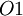 до
до 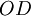 . Больший индекс соответствует старшему разряду.
. Больший индекс соответствует старшему разряду. 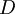 столбцов рассматриваются от
столбцов рассматриваются от 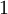 до
до 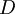 , причем столбец
, причем столбец 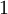 принимает младший вход.
принимает младший вход. 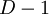 ступеней конвейера рассматриваются от
ступеней конвейера рассматриваются от 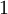 до
до 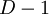 , причем входы схемы поступают на ступень
, причем входы схемы поступают на ступень 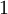 . Каждая ступень конвейера срабатывает за время
. Каждая ступень конвейера срабатывает за время 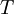 . Каждая ступень конвейера состоит из некоторого числа элементов ROMij и LATCH, на входы которых поступают выходы предыдущей ступени, а выходы передаются на входы следующей ступени. Элемент с индексами i.j - это ROMij, если
. Каждая ступень конвейера состоит из некоторого числа элементов ROMij и LATCH, на входы которых поступают выходы предыдущей ступени, а выходы передаются на входы следующей ступени. Элемент с индексами i.j - это ROMij, если 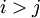 , или LATCH, в противном случае. Левый вход элемента ROMij -
, или LATCH, в противном случае. Левый вход элемента ROMij -  , правый -
, правый - 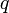 .
.
Для произвольного значения 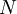 схема сокращенного преобразователя в полиадический код - это конвейерная схема из
схема сокращенного преобразователя в полиадический код - это конвейерная схема из 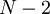 ступеней, содержащая
ступеней, содержащая 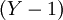 элементов ROMij и
элементов ROMij и 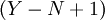 элементов LATCH, где
элементов LATCH, где 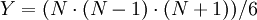 . Входом схемы являются
. Входом схемы являются 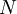 цифр модулярного представления, выходом -
цифр модулярного представления, выходом - 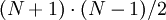 цифр полиадического кода. Данная реализация преобразователя заключает в себе
цифр полиадического кода. Данная реализация преобразователя заключает в себе 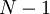 подсхем преобразователя в полиадический код, от
подсхем преобразователя в полиадический код, от 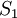 до
до 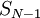 . Подсхема
. Подсхема 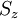 содержит
содержит 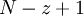 элементов. Элемент ROMij, находящийся в столбце
элементов. Элемент ROMij, находящийся в столбце 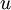 , ступени
, ступени 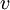 подсхемы
подсхемы 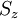 определяется так:
определяется так:
-
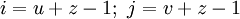 .
.
Входами подсхемы 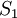 являются цифры от
являются цифры от 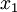 до
до 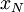 . Подсхема
. Подсхема 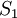 представляет собой особый случай, поскольку сокращена на одну ступень, ее выходы формируются после
представляет собой особый случай, поскольку сокращена на одну ступень, ее выходы формируются после 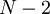 ступени: это цифры полиадического кода от
ступени: это цифры полиадического кода от 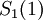 до
до 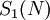 .
.
Входами подсхемы 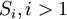 являются
являются 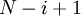 p-входов
p-входов 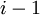 ступени подсхемы
ступени подсхемы 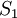 . Выходы подсхемы
. Выходы подсхемы 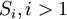 : от
: от 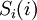 до
до 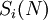 .
.
Выходы рассмотренной схемы преобразователя необходимы и достаточны для того, чтобы получить полиадическое представление всех проекций. Цифры полиадического кода проекции 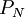 таковы: от
таковы: от 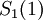 до
до 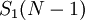 . Цифры полиадического кода проекции
. Цифры полиадического кода проекции 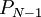 таковы: от
таковы: от 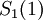 до
до 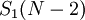 , и
, и 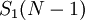 .
.
Цифры полиадического кода проекции 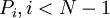 таковы: от
таковы: от 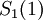 до
до 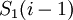 , если
, если 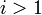 , и от
, и от 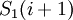 до
до 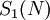 .
.
Данный преобразователь может быть реализован следующим образом:
Во-первых, при помощи преобразования в полиадический код определяются 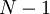 цифр полиадического кода, которые должны быть вычислены для каждой из
цифр полиадического кода, которые должны быть вычислены для каждой из 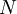 проекций. Затем каждая из цифр выражается через элементы, необходимые для ее вычисления.
проекций. Затем каждая из цифр выражается через элементы, необходимые для ее вычисления.
Во-вторых, выявляются уникальные подформулы.
В-третьих, первая ступень преобразователя строится размещением и соединением элементов, соответствующих уникальным подформулам первого порядка (наибольшей вложенности).
В-четвертых, вторая ступень преобразователя строится размещением и соединением элементов, соответствующих уникальным подформулам второго порядка.
Процесс продолжается до тех пор, пока не будут построены все 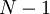 ступеней. Затем там, где необходимо, добавляются элементы LATCH, чтобы передать все цифры полиадического кода до конца конвейера.
ступеней. Затем там, где необходимо, добавляются элементы LATCH, чтобы передать все цифры полиадического кода до конца конвейера.
Простой метод, основанный на репликации, требует 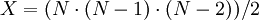 LUT и ROM. Сокращенный метод требует
LUT и ROM. Сокращенный метод требует 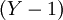 ROM и
ROM и 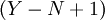 LUT, где
LUT, где 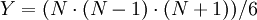 . Количество уровней обоих методов совпадает, и для реализации используются одинаковые элементы, поэтому тактовая частота работы после сокращения площади не изменится.
. Количество уровней обоих методов совпадает, и для реализации используются одинаковые элементы, поэтому тактовая частота работы после сокращения площади не изменится.
| N | 4 | 5 | 6 | 7 | 10 |
| Репликация (кол-во ROM/LUT) | 12 | 30 | 60 | 105 | 360 |
| Метод сокращения (кол-во ROM) | 9 | 19 | 34 | 55 | 164 |
| Метод сокращения (кол-во LUT) | 7 | 16 | 30 | 50 | 156 |
Ссылки
- [1] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York.
- [2] Патент "Efficient structure for computing mixed-radix projections from residue number systems"