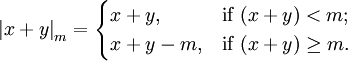–Ď–ł–ľ–ĺ–ī—É–Ľ—Ć–Ĺ–į—Ź –ľ–ĺ–ī—É–Ľ—Ź—Ä–Ĺ–į—Ź –į—Ä–ł—Ą–ľ–Ķ—ā–ł–ļ–į
| –°—ā—Ä–ĺ–ļ–į 7: | –°—ā—Ä–ĺ–ļ–į 7: | ||
= –ö–ĺ–ī–ĺ–≤–į—Ź –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź –Ņ—Ä–ĺ—Ą. –Ē.–ź. –ü–ĺ—Ā–Ņ–Ķ–Ľ–ĺ–≤–į = | = –ö–ĺ–ī–ĺ–≤–į—Ź –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź –Ņ—Ä–ĺ—Ą. –Ē.–ź. –ü–ĺ—Ā–Ņ–Ķ–Ľ–ĺ–≤–į = | ||
| ‚ąí | –Ē–Ľ—Ź —ā–ĺ–≥–ĺ, —á—ā–ĺ–Ī—č —Ā–Ī–į–Ľ–į–Ĺ—Ā–ł—Ä–ĺ–≤–į—ā—Ć –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ –ľ–ĺ–ī—É–Ľ—Ć–Ĺ—č—Ö –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ –Ē.–ź. –ü–ĺ—Ā–Ņ–Ķ–Ľ–ĺ–≤ –≤–≤–Ķ–Ľ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –ł—Ā—Ö–ĺ–ī–Ĺ—č—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤ –≤ –≤–ł–ī–Ķ –Ņ–į—Ä <math> <|x|_p, ind_w|x|_p> </math>>, –≥–ī–Ķ <math> |x|_p </math> –Ķ—Ā—ā—Ć –≤—č—á–Ķ—ā <math> x </math> –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é <math> p </math> , <math> i = ind_w|x|_p </math> - —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ļ –≤—č—á–Ķ—ā—É <math> |x|_p </math> –ł–Ĺ–ī–Ķ–ļ—Ā, –Ņ—Ä–ł —ć—ā–ĺ–ľ —É—Ā–Ľ–ĺ–≤–Ĺ–ĺ —Ā—á–ł—ā–į–Ķ—ā—Ā—Ź, —á—ā–ĺ –≤—č—á–Ķ—ā—É 0 —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É–Ķ—ā —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č–Ļ —Ā–ł–ľ–≤–ĺ–Ľ őĽ, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –ĺ–Ī–Ľ–į–ī–į–Ķ—ā —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ őĽ+i=i+őĽ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –ł–Ĺ–ī–Ķ–ļ—Ā–į <math> 0 | + | –Ē–Ľ—Ź —ā–ĺ–≥–ĺ, —á—ā–ĺ–Ī—č —Ā–Ī–į–Ľ–į–Ĺ—Ā–ł—Ä–ĺ–≤–į—ā—Ć –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ –ľ–ĺ–ī—É–Ľ—Ć–Ĺ—č—Ö –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ –Ē.–ź. –ü–ĺ—Ā–Ņ–Ķ–Ľ–ĺ–≤ –≤–≤–Ķ–Ľ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –ł—Ā—Ö–ĺ–ī–Ĺ—č—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤ –≤ –≤–ł–ī–Ķ –Ņ–į—Ä <math> <|x|_p, ind_w|x|_p> </math>>, –≥–ī–Ķ <math> |x|_p </math> –Ķ—Ā—ā—Ć –≤—č—á–Ķ—ā <math> x </math> –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é <math> p </math> , <math> i = ind_w|x|_p </math> - —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ļ –≤—č—á–Ķ—ā—É <math> |x|_p </math> –ł–Ĺ–ī–Ķ–ļ—Ā, –Ņ—Ä–ł —ć—ā–ĺ–ľ —É—Ā–Ľ–ĺ–≤–Ĺ–ĺ —Ā—á–ł—ā–į–Ķ—ā—Ā—Ź, —á—ā–ĺ –≤—č—á–Ķ—ā—É 0 —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É–Ķ—ā —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č–Ļ —Ā–ł–ľ–≤–ĺ–Ľ őĽ, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –ĺ–Ī–Ľ–į–ī–į–Ķ—ā —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ őĽ+i=i+őĽ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –ł–Ĺ–ī–Ķ–ļ—Ā–į <math> 0\le i\le p-2 </math> . –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –≤—Ā–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –Ņ–ĺ–Ľ—Ź –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź—é—ā—Ā—Ź –Ĺ–į–ī –Ņ–į—Ä–į–ľ–ł: –Ķ—Ā–Ľ–ł —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –Ĺ–į–Ļ—ā–ł —Ā—É–ľ–ľ—É –ī–≤—É—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é <math> p </math>, —ā–ĺ —Ā—É–ľ–ľ–ł—Ä—É—é—ā—Ā—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é <math> p </math> –Ņ–Ķ—Ä–≤—č–Ķ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä; –ī–Ľ—Ź —Ą–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –≤—ā–ĺ—Ä–ĺ–Ļ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä—č —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į —ć—ā–ĺ—ā —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–Ķ—ā—Ā—Ź –≤ –ł–Ĺ–ī–Ķ–ļ—Ā –Ņ—É—ā–Ķ–ľ –≤—č–Ī–ĺ—Ä–ļ–ł –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ł–∑ —ā–į–Ī–Ľ–ł—Ü—č –ł–Ĺ–ī–Ķ–ļ—Ā–ĺ–≤ (—Ä–ł—Ā.1). –ē—Ā–Ľ–ł —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –Ĺ–į–Ļ—ā–ł –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –ī–≤—É—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é <math> p </math>, —ā–ĺ —Ā—É–ľ–ľ–ł—Ä—É—é—ā—Ā—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é <math> p - 1 </math> –≤—ā–ĺ—Ä—č–Ķ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä; –ī–Ľ—Ź —Ą–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –Ņ–Ķ—Ä–≤–ĺ–Ļ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä—č —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į —ć—ā–ĺ—ā —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–Ķ—ā—Ā—Ź –≤ –į–Ĺ—ā–ł–Ľ–ĺ–≥–į—Ä–ł—Ą–ľ (–≤—č—á–Ķ—ā) –Ņ—É—ā–Ķ–ľ –≤—č–Ī–ĺ—Ä–ļ–ł –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ł–∑ —ā–į–Ī–Ľ–ł—Ü—č –≤—č—á–Ķ—ā–ĺ–≤ (—Ä–ł—Ā.2): |
| –°—ā—Ä–ĺ–ļ–į 18: | –°—ā—Ä–ĺ–ļ–į 18: | ||
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź —Ā–≤–Ķ–ī–Ķ–Ĺ—č –ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł—Ź–ľ —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é <math> p </math> –ł –ľ–ĺ–ī—É–Ľ—é <math> p-1 </math>, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, –ł –ĺ–ī–Ĺ–ĺ–Ļ —ā–į–Ī–Ľ–ł—á–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –≤—č–Ī–ĺ—Ä–į –≤—ā–ĺ—Ä–ĺ–Ļ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä—č —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į. –Ę–į–ļ–ĺ–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā —Ā–ĺ–ļ—Ä–į—ā–ł—ā—Ć –≤—Ä–Ķ–ľ—Ź –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł—Ź –ľ—É–Ľ—Ć—ā–ł–Ņ–Ľ–ł–ļ–į—ā–ł–≤–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –Ĺ–į –ĺ–ī–ł–Ĺ —ā–į–ļ—ā —ā–į–Ī–Ľ–ł—á–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –ł –Ņ–Ľ–ĺ—Č–į–ī—Ć –Ĺ–į —Ö—Ä–į–Ĺ–Ķ–Ĺ–ł–Ķ –ī–≤—É—Ö —ā–į–Ī–Ľ–ł—Ü –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź –≤ –ł–Ĺ–ī–Ķ–ļ—Ā—č, —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā—Ć –ļ–į–∂–ī–ĺ–Ļ —ā–į–Ī–Ľ–ł—Ü—č <math>2(p-1)</math>. –ü—Ä–ł —ć—ā–ĺ–ľ, –Ē.–ź. –ü–ĺ—Ā–Ņ–Ķ–Ľ–ĺ–≤ —É—ā–≤–Ķ—Ä–∂–ī–į–Ķ—ā [1, —Ā—ā—Ä. 296], —á—ā–ĺ, –Ĺ–Ķ—Ā–ľ–ĺ—ā—Ä—Ź –Ĺ–į —ā–ĺ, —á—ā–ĺ –Ľ–ĺ–≥–ł–ļ–į –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é <math> p </math> —Ā—ā–į–Ľ–į –Ī–ĺ–Ľ–Ķ–Ķ —Ā–Ľ–ĺ–∂–Ĺ–ĺ–Ļ, —á–Ķ–ľ –≤ –ĺ–Ī—č—á–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ļ–ĺ–ī–į –≤ –ĺ—Ā—ā–į—ā–ļ–į—Ö, –≤—č–ł–≥—Ä—č—ą —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤ ¬ę–ĺ–ī–Ĺ–ĺ—ā–ł–Ņ–Ĺ–ĺ—Ā—ā–ł –ĺ–Ī–ĺ—Ä—É–ī–ĺ–≤–į–Ĺ–ł—Ź –ī–Ľ—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–į –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź¬Ľ. –Ē–į–Ĺ–Ĺ–ĺ–Ķ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–ĺ –≤ –ĺ–Ī—Č–Ķ–ľ —Ā–Ľ—É—á–į–Ķ, –ļ–ĺ–≥–ī–į —Ā—É–ľ–ľ–į—ā–ĺ—Ä—č –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—Ź–ľ <math> p </math> –ł <math> (p-1) </math> –Ņ—Ä–ĺ–Ķ–ļ—ā–ł—Ä—É—é—ā—Ā—Ź –Ņ–ĺ –ľ–Ķ—ā–ĺ–ī—É –Ņ—Ä—Ź–ľ–ĺ–Ļ –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ –ī–≤–ĺ–ł—á–Ĺ—č—Ö —Ą—É–Ĺ–ļ—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č—Ö –Ī–Ľ–ĺ–ļ–ĺ–≤. –í —ć—ā–ĺ–ľ —Ā–Ľ—É—á–į–Ķ —Ā—É–ľ–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é <math> m </math> –ī–Ľ—Ź –ī–≤—É—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤ <math> x </math> –ł <math> y </math>, –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł—Ö—Ā—Ź –≤ –ī–ł–į–Ņ–į–∑–ĺ–Ĺ–Ķ <math>{0, 1,\ldots, m-1}</math>, –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ: | –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź —Ā–≤–Ķ–ī–Ķ–Ĺ—č –ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł—Ź–ľ —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é <math> p </math> –ł –ľ–ĺ–ī—É–Ľ—é <math> p-1 </math>, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, –ł –ĺ–ī–Ĺ–ĺ–Ļ —ā–į–Ī–Ľ–ł—á–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –≤—č–Ī–ĺ—Ä–į –≤—ā–ĺ—Ä–ĺ–Ļ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä—č —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į. –Ę–į–ļ–ĺ–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā —Ā–ĺ–ļ—Ä–į—ā–ł—ā—Ć –≤—Ä–Ķ–ľ—Ź –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł—Ź –ľ—É–Ľ—Ć—ā–ł–Ņ–Ľ–ł–ļ–į—ā–ł–≤–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –Ĺ–į –ĺ–ī–ł–Ĺ —ā–į–ļ—ā —ā–į–Ī–Ľ–ł—á–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –ł –Ņ–Ľ–ĺ—Č–į–ī—Ć –Ĺ–į —Ö—Ä–į–Ĺ–Ķ–Ĺ–ł–Ķ –ī–≤—É—Ö —ā–į–Ī–Ľ–ł—Ü –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź –≤ –ł–Ĺ–ī–Ķ–ļ—Ā—č, —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā—Ć –ļ–į–∂–ī–ĺ–Ļ —ā–į–Ī–Ľ–ł—Ü—č <math>2(p-1)</math>. –ü—Ä–ł —ć—ā–ĺ–ľ, –Ē.–ź. –ü–ĺ—Ā–Ņ–Ķ–Ľ–ĺ–≤ —É—ā–≤–Ķ—Ä–∂–ī–į–Ķ—ā [1, —Ā—ā—Ä. 296], —á—ā–ĺ, –Ĺ–Ķ—Ā–ľ–ĺ—ā—Ä—Ź –Ĺ–į —ā–ĺ, —á—ā–ĺ –Ľ–ĺ–≥–ł–ļ–į –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é <math> p </math> —Ā—ā–į–Ľ–į –Ī–ĺ–Ľ–Ķ–Ķ —Ā–Ľ–ĺ–∂–Ĺ–ĺ–Ļ, —á–Ķ–ľ –≤ –ĺ–Ī—č—á–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ļ–ĺ–ī–į –≤ –ĺ—Ā—ā–į—ā–ļ–į—Ö, –≤—č–ł–≥—Ä—č—ą —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤ ¬ę–ĺ–ī–Ĺ–ĺ—ā–ł–Ņ–Ĺ–ĺ—Ā—ā–ł –ĺ–Ī–ĺ—Ä—É–ī–ĺ–≤–į–Ĺ–ł—Ź –ī–Ľ—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–į –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź¬Ľ. –Ē–į–Ĺ–Ĺ–ĺ–Ķ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–ĺ –≤ –ĺ–Ī—Č–Ķ–ľ —Ā–Ľ—É—á–į–Ķ, –ļ–ĺ–≥–ī–į —Ā—É–ľ–ľ–į—ā–ĺ—Ä—č –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—Ź–ľ <math> p </math> –ł <math> (p-1) </math> –Ņ—Ä–ĺ–Ķ–ļ—ā–ł—Ä—É—é—ā—Ā—Ź –Ņ–ĺ –ľ–Ķ—ā–ĺ–ī—É –Ņ—Ä—Ź–ľ–ĺ–Ļ –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ –ī–≤–ĺ–ł—á–Ĺ—č—Ö —Ą—É–Ĺ–ļ—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č—Ö –Ī–Ľ–ĺ–ļ–ĺ–≤. –í —ć—ā–ĺ–ľ —Ā–Ľ—É—á–į–Ķ —Ā—É–ľ–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é <math> m </math> –ī–Ľ—Ź –ī–≤—É—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤ <math> x </math> –ł <math> y </math>, –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł—Ö—Ā—Ź –≤ –ī–ł–į–Ņ–į–∑–ĺ–Ĺ–Ķ <math>{0, 1,\ldots, m-1}</math>, –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ: | ||
| ‚ąí | + | :<math>{|x+y|}_m = \begin{cases} | |
| + | x+y, & \mbox{if } (x+y) < m ; \\ | ||
| + | x+y-m, & \mbox{if } (x+y) \ge m. | ||
| + | \end{cases} | ||
| + | </math> | ||
= –ú–ĺ–ī–ł—Ą–ł—Ü–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–į—Ź –ļ–ĺ–ī–ĺ–≤–į—Ź –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź = | = –ú–ĺ–ī–ł—Ą–ł—Ü–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–į—Ź –ļ–ĺ–ī–ĺ–≤–į—Ź –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź = | ||
–í–Ķ—Ä—Ā–ł—Ź 16:35, 28 –ľ–į—Ź 2014
–ź–ī–ī–ł—ā–ł–≤–Ĺ—č–Ļ —Ö–į—Ä–į–ļ—ā–Ķ—Ä –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł–Ļ –≤ –ļ–ĺ–Ľ—Ć—Ü–Ķ –≤—č—á–Ķ—ā–ĺ–≤ 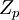 –Ņ–ĺ—Ä–ĺ–∂–ī–į–Ķ—ā –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —Ä–į—Ā—Ö–ĺ–ī—č –Ĺ–į –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ –į—Ä–ł—Ą–ľ–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ. –≠—ā–ĺ –ĺ–Ī—É—Ā–Ľ–ĺ–≤–Ľ–Ķ–Ĺ–ĺ —ā–Ķ–ľ, —á—ā–ĺ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –ľ–ĺ–∂–Ķ—ā –≤—č–Ļ—ā–ł –∑–į –ī–ł–į–Ņ–į–∑–ĺ–Ĺ
–Ņ–ĺ—Ä–ĺ–∂–ī–į–Ķ—ā –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —Ä–į—Ā—Ö–ĺ–ī—č –Ĺ–į –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ –į—Ä–ł—Ą–ľ–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ. –≠—ā–ĺ –ĺ–Ī—É—Ā–Ľ–ĺ–≤–Ľ–Ķ–Ĺ–ĺ —ā–Ķ–ľ, —á—ā–ĺ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –ľ–ĺ–∂–Ķ—ā –≤—č–Ļ—ā–ł –∑–į –ī–ł–į–Ņ–į–∑–ĺ–Ĺ 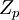 , —ā–ĺ–≥–ī–į —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –ļ–ĺ—Ä—Ä–Ķ–ļ—ā–ł—Ä–ĺ–≤–ļ–į —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į, —ā.–Ķ. –≤–∑—Ź—ā–ł–Ķ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é. –ú—É–Ľ—Ć—ā–ł–Ņ–Ľ–ł–ļ–į—ā–ł–≤–Ĺ–į—Ź –ĺ–Ņ–Ķ—Ä–į—Ü–ł—Ź –Ĺ–į–ī –ĺ—Ā—ā–į—ā–ļ–į–ľ–ł x, y mod p –Ī–ĺ–Ľ–Ķ–Ķ —ā—Ä—É–ī–ĺ–Ķ–ľ–ļ–į, –Ņ–ĺ—ć—ā–ĺ–ľ—É –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ —ć—Ą—Ą–Ķ–ļ—ā–ł–≤–Ĺ—č–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–ĺ–ľ –ł–∑–Ī–Ķ–∂–į—ā—Ć –Ņ—Ä—Ź–ľ–ĺ–Ļ —Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł –ľ—É–Ľ—Ć—ā–ł–Ņ–Ľ–ł–ļ–į—ā–ł–≤–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī –ļ –ł–Ĺ–ī–Ķ–ļ—Ā–į–ľ –≤—č—á–Ķ—ā–ĺ–≤ –Ņ–ĺ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—é –Ņ–Ķ—Ä–≤–ĺ–ĺ–Ī—Ä–į–∑–Ĺ–ĺ–≥–ĺ –ļ–ĺ—Ä–Ĺ—Ź, –ĺ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ —Ā–≤—Ź–∑–į–Ĺ–Ĺ—č—Ö —Ā –ī–į–Ĺ–Ĺ—č–ľ –ľ–ĺ–ī—É–Ľ—Ź—Ä–Ĺ—č–ľ –ļ–ĺ–ī–ĺ–ľ.
, —ā–ĺ–≥–ī–į —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –ļ–ĺ—Ä—Ä–Ķ–ļ—ā–ł—Ä–ĺ–≤–ļ–į —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į, —ā.–Ķ. –≤–∑—Ź—ā–ł–Ķ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é. –ú—É–Ľ—Ć—ā–ł–Ņ–Ľ–ł–ļ–į—ā–ł–≤–Ĺ–į—Ź –ĺ–Ņ–Ķ—Ä–į—Ü–ł—Ź –Ĺ–į–ī –ĺ—Ā—ā–į—ā–ļ–į–ľ–ł x, y mod p –Ī–ĺ–Ľ–Ķ–Ķ —ā—Ä—É–ī–ĺ–Ķ–ľ–ļ–į, –Ņ–ĺ—ć—ā–ĺ–ľ—É –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ —ć—Ą—Ą–Ķ–ļ—ā–ł–≤–Ĺ—č–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–ĺ–ľ –ł–∑–Ī–Ķ–∂–į—ā—Ć –Ņ—Ä—Ź–ľ–ĺ–Ļ —Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł –ľ—É–Ľ—Ć—ā–ł–Ņ–Ľ–ł–ļ–į—ā–ł–≤–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī –ļ –ł–Ĺ–ī–Ķ–ļ—Ā–į–ľ –≤—č—á–Ķ—ā–ĺ–≤ –Ņ–ĺ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—é –Ņ–Ķ—Ä–≤–ĺ–ĺ–Ī—Ä–į–∑–Ĺ–ĺ–≥–ĺ –ļ–ĺ—Ä–Ĺ—Ź, –ĺ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ —Ā–≤—Ź–∑–į–Ĺ–Ĺ—č—Ö —Ā –ī–į–Ĺ–Ĺ—č–ľ –ľ–ĺ–ī—É–Ľ—Ź—Ä–Ĺ—č–ľ –ļ–ĺ–ī–ĺ–ľ.
–í —Ā–Ľ—É—á–į–Ķ –ł–Ĺ–ī–Ķ–ļ—Ā–Ĺ–ĺ–Ļ –į—Ä–ł—Ą–ľ–Ķ—ā–ł–ļ–ł –ĺ–Ņ–Ķ—Ä–į—Ü–ł—Ź ¬ę+¬Ľ –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ—ā—Ā—Ź –∑–į –ĺ–ī–ł–Ĺ —ā–į–ļ—ā –ľ–ĺ–ī—É–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ā—É–ľ–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź, –į –ĺ–Ņ–Ķ—Ä–į—Ü–ł—Ź ¬ę*¬Ľ –∑–į —ā–į–ļ—ā –ľ–ĺ–ī—É–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ā—É–ľ–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –ł –ī–≤–į —ā–į–ļ—ā–į —ā–į–Ī–Ľ–ł—á–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł.
–ö–ĺ–ī–ĺ–≤–į—Ź –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź –Ņ—Ä–ĺ—Ą. –Ē.–ź. –ü–ĺ—Ā–Ņ–Ķ–Ľ–ĺ–≤–į
–Ē–Ľ—Ź —ā–ĺ–≥–ĺ, —á—ā–ĺ–Ī—č —Ā–Ī–į–Ľ–į–Ĺ—Ā–ł—Ä–ĺ–≤–į—ā—Ć –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ –ľ–ĺ–ī—É–Ľ—Ć–Ĺ—č—Ö –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ –Ē.–ź. –ü–ĺ—Ā–Ņ–Ķ–Ľ–ĺ–≤ –≤–≤–Ķ–Ľ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –ł—Ā—Ö–ĺ–ī–Ĺ—č—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤ –≤ –≤–ł–ī–Ķ –Ņ–į—Ä 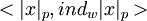 >, –≥–ī–Ķ
>, –≥–ī–Ķ 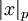 –Ķ—Ā—ā—Ć –≤—č—á–Ķ—ā
–Ķ—Ā—ā—Ć –≤—č—á–Ķ—ā  –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é
–Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é  ,
, 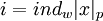 - —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ļ –≤—č—á–Ķ—ā—É
- —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ļ –≤—č—á–Ķ—ā—É 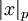 –ł–Ĺ–ī–Ķ–ļ—Ā, –Ņ—Ä–ł —ć—ā–ĺ–ľ —É—Ā–Ľ–ĺ–≤–Ĺ–ĺ —Ā—á–ł—ā–į–Ķ—ā—Ā—Ź, —á—ā–ĺ –≤—č—á–Ķ—ā—É 0 —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É–Ķ—ā —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č–Ļ —Ā–ł–ľ–≤–ĺ–Ľ őĽ, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –ĺ–Ī–Ľ–į–ī–į–Ķ—ā —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ őĽ+i=i+őĽ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –ł–Ĺ–ī–Ķ–ļ—Ā–į
–ł–Ĺ–ī–Ķ–ļ—Ā, –Ņ—Ä–ł —ć—ā–ĺ–ľ —É—Ā–Ľ–ĺ–≤–Ĺ–ĺ —Ā—á–ł—ā–į–Ķ—ā—Ā—Ź, —á—ā–ĺ –≤—č—á–Ķ—ā—É 0 —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É–Ķ—ā —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č–Ļ —Ā–ł–ľ–≤–ĺ–Ľ őĽ, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –ĺ–Ī–Ľ–į–ī–į–Ķ—ā —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ őĽ+i=i+őĽ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –ł–Ĺ–ī–Ķ–ļ—Ā–į 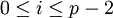 . –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –≤—Ā–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –Ņ–ĺ–Ľ—Ź –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź—é—ā—Ā—Ź –Ĺ–į–ī –Ņ–į—Ä–į–ľ–ł: –Ķ—Ā–Ľ–ł —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –Ĺ–į–Ļ—ā–ł —Ā—É–ľ–ľ—É –ī–≤—É—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é
. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –≤—Ā–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –Ņ–ĺ–Ľ—Ź –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź—é—ā—Ā—Ź –Ĺ–į–ī –Ņ–į—Ä–į–ľ–ł: –Ķ—Ā–Ľ–ł —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –Ĺ–į–Ļ—ā–ł —Ā—É–ľ–ľ—É –ī–≤—É—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é  , —ā–ĺ —Ā—É–ľ–ľ–ł—Ä—É—é—ā—Ā—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é
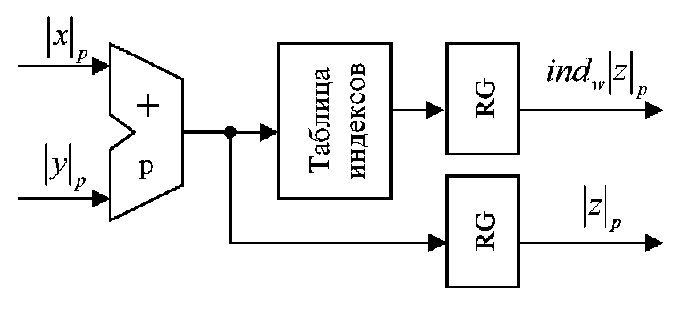
, —ā–ĺ —Ā—É–ľ–ľ–ł—Ä—É—é—ā—Ā—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é  –Ņ–Ķ—Ä–≤—č–Ķ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä; –ī–Ľ—Ź —Ą–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –≤—ā–ĺ—Ä–ĺ–Ļ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä—č —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į —ć—ā–ĺ—ā —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–Ķ—ā—Ā—Ź –≤ –ł–Ĺ–ī–Ķ–ļ—Ā –Ņ—É—ā–Ķ–ľ –≤—č–Ī–ĺ—Ä–ļ–ł –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ł–∑ —ā–į–Ī–Ľ–ł—Ü—č –ł–Ĺ–ī–Ķ–ļ—Ā–ĺ–≤ (—Ä–ł—Ā.1). –ē—Ā–Ľ–ł —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –Ĺ–į–Ļ—ā–ł –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –ī–≤—É—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é
–Ņ–Ķ—Ä–≤—č–Ķ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä; –ī–Ľ—Ź —Ą–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –≤—ā–ĺ—Ä–ĺ–Ļ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä—č —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į —ć—ā–ĺ—ā —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–Ķ—ā—Ā—Ź –≤ –ł–Ĺ–ī–Ķ–ļ—Ā –Ņ—É—ā–Ķ–ľ –≤—č–Ī–ĺ—Ä–ļ–ł –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ł–∑ —ā–į–Ī–Ľ–ł—Ü—č –ł–Ĺ–ī–Ķ–ļ—Ā–ĺ–≤ (—Ä–ł—Ā.1). –ē—Ā–Ľ–ł —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –Ĺ–į–Ļ—ā–ł –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –ī–≤—É—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é  , —ā–ĺ —Ā—É–ľ–ľ–ł—Ä—É—é—ā—Ā—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é
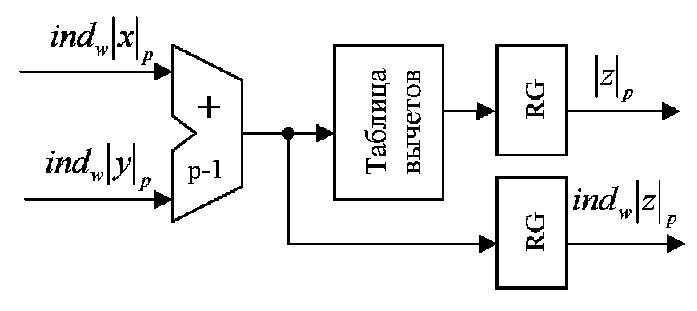
, —ā–ĺ —Ā—É–ľ–ľ–ł—Ä—É—é—ā—Ā—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é 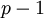 –≤—ā–ĺ—Ä—č–Ķ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä; –ī–Ľ—Ź —Ą–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –Ņ–Ķ—Ä–≤–ĺ–Ļ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä—č —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į —ć—ā–ĺ—ā —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–Ķ—ā—Ā—Ź –≤ –į–Ĺ—ā–ł–Ľ–ĺ–≥–į—Ä–ł—Ą–ľ (–≤—č—á–Ķ—ā) –Ņ—É—ā–Ķ–ľ –≤—č–Ī–ĺ—Ä–ļ–ł –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ł–∑ —ā–į–Ī–Ľ–ł—Ü—č –≤—č—á–Ķ—ā–ĺ–≤ (—Ä–ł—Ā.2):
–≤—ā–ĺ—Ä—č–Ķ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä; –ī–Ľ—Ź —Ą–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –Ņ–Ķ—Ä–≤–ĺ–Ļ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä—č —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į —ć—ā–ĺ—ā —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–Ķ—ā—Ā—Ź –≤ –į–Ĺ—ā–ł–Ľ–ĺ–≥–į—Ä–ł—Ą–ľ (–≤—č—á–Ķ—ā) –Ņ—É—ā–Ķ–ľ –≤—č–Ī–ĺ—Ä–ļ–ł –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ł–∑ —ā–į–Ī–Ľ–ł—Ü—č –≤—č—á–Ķ—ā–ĺ–≤ (—Ä–ł—Ā.2):
–ź—Ä–ł—Ą–ľ–Ķ—ā–ł–ļ—É, –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–Ĺ—É—é –Ĺ–į –Ņ–į—Ä–Ĺ–ĺ–ľ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–ł –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤, –Ī—É–ī–Ķ–ľ –Ĺ–į–∑—č–≤–į—ā—Ć –Ī–ł–ľ–ĺ–ī—É–Ľ—Ć–Ĺ–ĺ–Ļ –į—Ä–ł—Ą–ľ–Ķ—ā–ł–ļ–ĺ–Ļ –Ņ–ĺ–Ľ—Ź 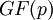 .
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź —Ā–≤–Ķ–ī–Ķ–Ĺ—č –ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł—Ź–ľ —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é
.
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź —Ā–≤–Ķ–ī–Ķ–Ĺ—č –ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł—Ź–ľ —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é  –ł –ľ–ĺ–ī—É–Ľ—é
–ł –ľ–ĺ–ī—É–Ľ—é 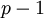 , —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, –ł –ĺ–ī–Ĺ–ĺ–Ļ —ā–į–Ī–Ľ–ł—á–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –≤—č–Ī–ĺ—Ä–į –≤—ā–ĺ—Ä–ĺ–Ļ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä—č —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į. –Ę–į–ļ–ĺ–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā —Ā–ĺ–ļ—Ä–į—ā–ł—ā—Ć –≤—Ä–Ķ–ľ—Ź –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł—Ź –ľ—É–Ľ—Ć—ā–ł–Ņ–Ľ–ł–ļ–į—ā–ł–≤–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –Ĺ–į –ĺ–ī–ł–Ĺ —ā–į–ļ—ā —ā–į–Ī–Ľ–ł—á–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –ł –Ņ–Ľ–ĺ—Č–į–ī—Ć –Ĺ–į —Ö—Ä–į–Ĺ–Ķ–Ĺ–ł–Ķ –ī–≤—É—Ö —ā–į–Ī–Ľ–ł—Ü –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź –≤ –ł–Ĺ–ī–Ķ–ļ—Ā—č, —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā—Ć –ļ–į–∂–ī–ĺ–Ļ —ā–į–Ī–Ľ–ł—Ü—č
, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, –ł –ĺ–ī–Ĺ–ĺ–Ļ —ā–į–Ī–Ľ–ł—á–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –≤—č–Ī–ĺ—Ä–į –≤—ā–ĺ—Ä–ĺ–Ļ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—č –Ņ–į—Ä—č —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į. –Ę–į–ļ–ĺ–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā —Ā–ĺ–ļ—Ä–į—ā–ł—ā—Ć –≤—Ä–Ķ–ľ—Ź –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł—Ź –ľ—É–Ľ—Ć—ā–ł–Ņ–Ľ–ł–ļ–į—ā–ł–≤–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –Ĺ–į –ĺ–ī–ł–Ĺ —ā–į–ļ—ā —ā–į–Ī–Ľ–ł—á–Ĺ–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –ł –Ņ–Ľ–ĺ—Č–į–ī—Ć –Ĺ–į —Ö—Ä–į–Ĺ–Ķ–Ĺ–ł–Ķ –ī–≤—É—Ö —ā–į–Ī–Ľ–ł—Ü –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź –≤ –ł–Ĺ–ī–Ķ–ļ—Ā—č, —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā—Ć –ļ–į–∂–ī–ĺ–Ļ —ā–į–Ī–Ľ–ł—Ü—č 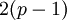 . –ü—Ä–ł —ć—ā–ĺ–ľ, –Ē.–ź. –ü–ĺ—Ā–Ņ–Ķ–Ľ–ĺ–≤ —É—ā–≤–Ķ—Ä–∂–ī–į–Ķ—ā [1, —Ā—ā—Ä. 296], —á—ā–ĺ, –Ĺ–Ķ—Ā–ľ–ĺ—ā—Ä—Ź –Ĺ–į —ā–ĺ, —á—ā–ĺ –Ľ–ĺ–≥–ł–ļ–į –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é
. –ü—Ä–ł —ć—ā–ĺ–ľ, –Ē.–ź. –ü–ĺ—Ā–Ņ–Ķ–Ľ–ĺ–≤ —É—ā–≤–Ķ—Ä–∂–ī–į–Ķ—ā [1, —Ā—ā—Ä. 296], —á—ā–ĺ, –Ĺ–Ķ—Ā–ľ–ĺ—ā—Ä—Ź –Ĺ–į —ā–ĺ, —á—ā–ĺ –Ľ–ĺ–≥–ł–ļ–į –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é  —Ā—ā–į–Ľ–į –Ī–ĺ–Ľ–Ķ–Ķ —Ā–Ľ–ĺ–∂–Ĺ–ĺ–Ļ, —á–Ķ–ľ –≤ –ĺ–Ī—č—á–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ļ–ĺ–ī–į –≤ –ĺ—Ā—ā–į—ā–ļ–į—Ö, –≤—č–ł–≥—Ä—č—ą —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤ ¬ę–ĺ–ī–Ĺ–ĺ—ā–ł–Ņ–Ĺ–ĺ—Ā—ā–ł –ĺ–Ī–ĺ—Ä—É–ī–ĺ–≤–į–Ĺ–ł—Ź –ī–Ľ—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–į –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź¬Ľ. –Ē–į–Ĺ–Ĺ–ĺ–Ķ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–ĺ –≤ –ĺ–Ī—Č–Ķ–ľ —Ā–Ľ—É—á–į–Ķ, –ļ–ĺ–≥–ī–į —Ā—É–ľ–ľ–į—ā–ĺ—Ä—č –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—Ź–ľ
—Ā—ā–į–Ľ–į –Ī–ĺ–Ľ–Ķ–Ķ —Ā–Ľ–ĺ–∂–Ĺ–ĺ–Ļ, —á–Ķ–ľ –≤ –ĺ–Ī—č—á–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ļ–ĺ–ī–į –≤ –ĺ—Ā—ā–į—ā–ļ–į—Ö, –≤—č–ł–≥—Ä—č—ą —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤ ¬ę–ĺ–ī–Ĺ–ĺ—ā–ł–Ņ–Ĺ–ĺ—Ā—ā–ł –ĺ–Ī–ĺ—Ä—É–ī–ĺ–≤–į–Ĺ–ł—Ź –ī–Ľ—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–į –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ł —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł—Ź¬Ľ. –Ē–į–Ĺ–Ĺ–ĺ–Ķ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–ĺ –≤ –ĺ–Ī—Č–Ķ–ľ —Ā–Ľ—É—á–į–Ķ, –ļ–ĺ–≥–ī–į —Ā—É–ľ–ľ–į—ā–ĺ—Ä—č –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—Ź–ľ  –ł
–ł 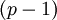 –Ņ—Ä–ĺ–Ķ–ļ—ā–ł—Ä—É—é—ā—Ā—Ź –Ņ–ĺ –ľ–Ķ—ā–ĺ–ī—É –Ņ—Ä—Ź–ľ–ĺ–Ļ –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ –ī–≤–ĺ–ł—á–Ĺ—č—Ö —Ą—É–Ĺ–ļ—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č—Ö –Ī–Ľ–ĺ–ļ–ĺ–≤. –í —ć—ā–ĺ–ľ —Ā–Ľ—É—á–į–Ķ —Ā—É–ľ–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é
–Ņ—Ä–ĺ–Ķ–ļ—ā–ł—Ä—É—é—ā—Ā—Ź –Ņ–ĺ –ľ–Ķ—ā–ĺ–ī—É –Ņ—Ä—Ź–ľ–ĺ–Ļ –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ –ī–≤–ĺ–ł—á–Ĺ—č—Ö —Ą—É–Ĺ–ļ—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č—Ö –Ī–Ľ–ĺ–ļ–ĺ–≤. –í —ć—ā–ĺ–ľ —Ā–Ľ—É—á–į–Ķ —Ā—É–ľ–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é  –ī–Ľ—Ź –ī–≤—É—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤
–ī–Ľ—Ź –ī–≤—É—Ö –ĺ–Ņ–Ķ—Ä–į–Ĺ–ī–ĺ–≤  –ł
–ł 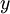 , –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł—Ö—Ā—Ź –≤ –ī–ł–į–Ņ–į–∑–ĺ–Ĺ–Ķ
, –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł—Ö—Ā—Ź –≤ –ī–ł–į–Ņ–į–∑–ĺ–Ĺ–Ķ 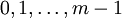 , –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ:
, –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ:
–ú–ĺ–ī–ł—Ą–ł—Ü–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–į—Ź –ļ–ĺ–ī–ĺ–≤–į—Ź –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź
–°—Ā—č–Ľ–ļ–ł
- [1] –ü–ĺ—Ā–Ņ–Ķ–Ľ–ĺ–≤ –Ē.–ź. –ź—Ä–ł—Ą–ľ–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–Ķ –ĺ—Ā–Ĺ–ĺ–≤—č –≤—č—á–ł—Ā–Ľ–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –ľ–į—ą–ł–Ĺ –ī–ł—Ā–ļ—Ä–Ķ—ā–Ĺ–ĺ–≥–ĺ –ī–Ķ–Ļ—Ā—ā–≤–ł—Ź. –ú.: –í—č—Ā—ą. —ą–ļ., 1970.