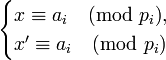–ö–Η―²–Α–Ι―¹–Κ–Α―è ―²–Β–Ψ―Ä–Β–Φ–Α –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö
| –Γ―²―Ä–Ψ–Κ–Α 38: | –Γ―²―Ä–Ψ–Κ–Α 38: | ||
–Γ–Η―¹―²–Β–Φ―É (*) –Φ–Ψ–Ε–Ϋ–Ψ ―Ä–Β―à–Η―²―¨ ―²–Α–Κ: | –Γ–Η―¹―²–Β–Φ―É (*) –Φ–Ψ–Ε–Ϋ–Ψ ―Ä–Β―à–Η―²―¨ ―²–Α–Κ: | ||
| β࣠| (1) –î–Μ―è <math>i=1,\ldots, k</math> –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ < | + | (1) –î–Μ―è <math>i=1,\ldots, k</math> –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ <math>z_i=p/p_i=p_1\cdot p_2\cdot\ldots\cdot p_{i-1}\cdot p_{i+1}\cdot \ldots\cdot p_k</math>. |
| β࣠| (2) –î–Μ―è <math>i=1,\ldots, k</math> –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ < | + | (2) –î–Μ―è <math>i=1,\ldots, k</math> –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ <math>y_i=z_{i}^{-1} \pmod{p_i}</math>. (–½–Α–Φ–Β―²–Η–Φ, ―΅―²–Ψ ―ç―²–Ψ –≤―¹–Β–≥–¥–Α –Φ–Ψ–Ε–Ϋ–Ψ ―¹–¥–Β–Μ–Α―²―¨, –Ω–Ψ―¹–Κ–Ψ–Μ―¨–Κ―É <math>(z_i, p_i)=1</math>. |
(3) –†–Β―à–Β–Ϋ–Η–Β–Φ ―¹–Η―¹―²–Β–Φ―΄ ―è–≤–Μ―è–Β―²―¹―è ―΅–Η―¹–Μ–Ψ <math>x=a_1\cdot y_1\cdot z_1 + \ldots +a_k\cdot y_k\cdot z_k=1</math>. | (3) –†–Β―à–Β–Ϋ–Η–Β–Φ ―¹–Η―¹―²–Β–Φ―΄ ―è–≤–Μ―è–Β―²―¹―è ―΅–Η―¹–Μ–Ψ <math>x=a_1\cdot y_1\cdot z_1 + \ldots +a_k\cdot y_k\cdot z_k=1</math>. | ||
–£–Β―Ä―¹–Η―è 14:47, 11 ―¹–Β–Ϋ―²―è–±―Ä―è 2014
–ö–Η―²–Α–Ι―¹–Κ–Α―è ―²–Β–Ψ―Ä–Β–Φ–Α –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö ―³–Ψ―Ä–Φ―É–Μ–Η―Ä―É–Β―²―¹―è ―¹–Μ–Β–¥―É―é―â–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ:
–Δ–Β–Ψ―Ä–Β–Φ–Α.
–ü―É―¹―²―¨ 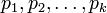 - –Ω–Ψ–Ω–Α―Ä–Ϋ–Ψ –≤–Ζ–Α–Η–Φ–Ϋ–Ψ –Ω―Ä–Ψ―¹―²―΄–Β ―΅–Η―¹–Μ–Α, –±–Ψ–Μ―¨―à–Η–Β 1, –Η –Ω―É―¹―²―¨
- –Ω–Ψ–Ω–Α―Ä–Ϋ–Ψ –≤–Ζ–Α–Η–Φ–Ϋ–Ψ –Ω―Ä–Ψ―¹―²―΄–Β ―΅–Η―¹–Μ–Α, –±–Ψ–Μ―¨―à–Η–Β 1, –Η –Ω―É―¹―²―¨ 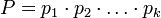 . –Δ–Ψ–≥–¥–Α ―¹―É―â–Β―¹―²–≤―É–Β―² –Β–¥–Η–Ϋ―¹―²–≤–Β–Ϋ–Ϋ–Ψ–Β –Ϋ–Β–Ψ―²―Ä–Η―Ü–Α―²–Β–Μ―¨–Ϋ–Ψ–Β ―Ä–Β―à–Β–Ϋ–Η–Β –Ω–Ψ –Φ–Ψ–¥―É–Μ―é
. –Δ–Ψ–≥–¥–Α ―¹―É―â–Β―¹―²–≤―É–Β―² –Β–¥–Η–Ϋ―¹―²–≤–Β–Ϋ–Ϋ–Ψ–Β –Ϋ–Β–Ψ―²―Ä–Η―Ü–Α―²–Β–Μ―¨–Ϋ–Ψ–Β ―Ä–Β―à–Β–Ϋ–Η–Β –Ω–Ψ –Φ–Ψ–¥―É–Μ―é 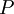 ―¹–Μ–Β–¥―É―é―â–Β–Ι ―¹–Η―¹―²–Β–Φ―΄ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι:
―¹–Μ–Β–¥―É―é―â–Β–Ι ―¹–Η―¹―²–Β–Φ―΄ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι:
-
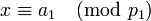 ,
,
-
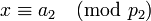 , (*)
, (*)
-
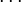 ,
,
-
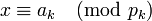 .
.
–î―Ä―É–≥–Η–Φ–Η ―¹–Μ–Ψ–≤–Α–Φ–Η, –Ψ―²–Ψ–±―Ä–Α–Ε–Β–Ϋ–Η–Β, –Κ–Ψ―²–Ψ―Ä–Ψ–Β –Κ–Α–Ε–¥–Ψ–Φ―É ―Ü–Β–Μ–Ψ–Φ―É ―΅–Η―¹–Μ―É 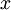 ,
, 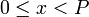 , ―¹―²–Α–≤–Η―² –≤ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Κ–Ψ―Ä―²–Β–Ε
, ―¹―²–Α–≤–Η―² –≤ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Κ–Ψ―Ä―²–Β–Ε 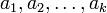 , –≥–¥–Β
, –≥–¥–Β 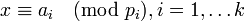 ―è–≤–Μ―è–Β―²―¹―è –±–Η–Β–Κ―Ü–Η–Β–Ι –Κ–Ψ–Μ―¨―Ü–Α
―è–≤–Μ―è–Β―²―¹―è –±–Η–Β–Κ―Ü–Η–Β–Ι –Κ–Ψ–Μ―¨―Ü–Α 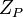 –Ϋ–Α –¥–Β–Κ–Α―Ä―²–Ψ–≤–Ψ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β
–Ϋ–Α –¥–Β–Κ–Α―Ä―²–Ψ–≤–Ψ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β 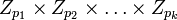 –Κ–Ψ–Μ–Β―Ü
–Κ–Ψ–Μ–Β―Ü 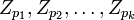 .
.
–Δ.–Β. ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Φ–Β–Ε–¥―É ―΅–Η―¹–Μ–Α–Φ–Η –Η –Κ–Ψ―Ä―²–Β–Ε–Α–Φ–Η ―è–≤–Μ―è–Β―²―¹―è –≤–Ζ–Α–Η–Φ–Ϋ–Ψ –Ψ–¥–Ϋ–Ψ–Ζ–Ϋ–Α―΅–Ϋ―΄–Φ, –Κ―Ä–Ψ–Φ–Β ―²–Ψ–≥–Ψ, –Ψ–Ω–Β―Ä–Α―Ü–Η–Η, –≤―΄–Ω–Ψ–Μ–Ϋ―è–Β–Φ―΄–Β –Ϋ–Α–¥ ―΅–Η―¹–Μ–Ψ–Φ  , –Φ–Ψ–Ε–Ϋ–Ψ ―ç–Κ–≤–Η–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ –≤―΄–Ω–Ψ–Μ–Ϋ―è―²―¨ –Ϋ–Α–¥ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤―É―é―â–Η–Φ–Η ―ç–Μ–Β–Φ–Β–Ϋ―²–Α–Φ–Η –Κ–Ψ―Ä―²–Β–Ε–Α–Φ–Η –Ω―É―²―ë–Φ –Ϋ–Β–Ζ–Α–≤–Η―¹–Η–Φ–Ψ–≥–Ψ –≤―΄–Ω–Ψ–Μ–Ϋ–Β–Ϋ–Η―è –Ψ–Ω–Β―Ä–Α―Ü–Η–Ι –Ϋ–Α–¥ –Κ–Α–Ε–¥―΄–Φ –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²–Ψ–Φ:
, –Φ–Ψ–Ε–Ϋ–Ψ ―ç–Κ–≤–Η–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ –≤―΄–Ω–Ψ–Μ–Ϋ―è―²―¨ –Ϋ–Α–¥ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤―É―é―â–Η–Φ–Η ―ç–Μ–Β–Φ–Β–Ϋ―²–Α–Φ–Η –Κ–Ψ―Ä―²–Β–Ε–Α–Φ–Η –Ω―É―²―ë–Φ –Ϋ–Β–Ζ–Α–≤–Η―¹–Η–Φ–Ψ–≥–Ψ –≤―΄–Ω–Ψ–Μ–Ϋ–Β–Ϋ–Η―è –Ψ–Ω–Β―Ä–Α―Ü–Η–Ι –Ϋ–Α–¥ –Κ–Α–Ε–¥―΄–Φ –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²–Ψ–Φ:
–Β―¹–Μ–Η
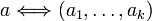 ,
,
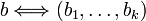 ,
,
―²–Ψ ―¹–Ω―Ä–Α–≤–Β–¥–Μ–Η–≤–Ψ:
-
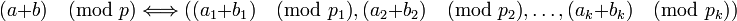 ,
,
-
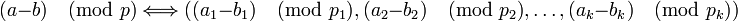 ,
,
-
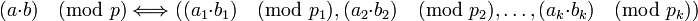 .
.
–Γ―É―â–Β―¹―²–≤―É–Β―² –Φ–Ϋ–Ψ–≥–Ψ ―Ä–Α–Ζ–Μ–Η―΅–Ϋ―΄―Ö –¥–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨―¹―²–≤ –Κ–Η―²–Α–Ι―¹–Κ–Ψ–Ι ―²–Β–Ψ―Ä–Β–Φ―΄ –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö. –ü―Ä–Η–≤–Β–¥―ë–Φ –Κ–Ψ–Ϋ―¹―²―Ä―É–Κ―²–Η–≤–Ϋ–Ψ–Β –¥–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨―¹―²–≤–Ψ ―ç―²–Ψ–Ι ―²–Β–Ψ―Ä–Β–Φ―΄.
–î–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨―¹―²–≤–Ψ ―¹―É―â–Β―¹―²–≤–Ψ–≤–Α–Ϋ–Η―è.
–î–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨―¹―²–≤–Ψ 1.
–Γ–Η―¹―²–Β–Φ―É (*) –Φ–Ψ–Ε–Ϋ–Ψ ―Ä–Β―à–Η―²―¨ ―²–Α–Κ:
(1) –î–Μ―è 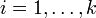 –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ
–Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ 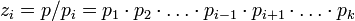 .
.
(2) –î–Μ―è 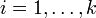 –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ
–Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ 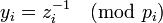 . (–½–Α–Φ–Β―²–Η–Φ, ―΅―²–Ψ ―ç―²–Ψ –≤―¹–Β–≥–¥–Α –Φ–Ψ–Ε–Ϋ–Ψ ―¹–¥–Β–Μ–Α―²―¨, –Ω–Ψ―¹–Κ–Ψ–Μ―¨–Κ―É
. (–½–Α–Φ–Β―²–Η–Φ, ―΅―²–Ψ ―ç―²–Ψ –≤―¹–Β–≥–¥–Α –Φ–Ψ–Ε–Ϋ–Ψ ―¹–¥–Β–Μ–Α―²―¨, –Ω–Ψ―¹–Κ–Ψ–Μ―¨–Κ―É 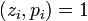 .
.
(3) –†–Β―à–Β–Ϋ–Η–Β–Φ ―¹–Η―¹―²–Β–Φ―΄ ―è–≤–Μ―è–Β―²―¹―è ―΅–Η―¹–Μ–Ψ 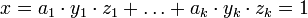 .
.
–î–Β–Ι―¹―²–≤–Η―²–Β–Μ―¨–Ϋ–Ψ, ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ –≤―΄―Ä–Α–Ε–Β–Ϋ–Η–Β –¥–Μ―è 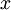 –Η –≤―΄―΅–Η―¹–Μ–Η–Φ, –Ϋ–Α–Ω―Ä–Η–Φ–Β―Ä,
–Η –≤―΄―΅–Η―¹–Μ–Η–Φ, –Ϋ–Α–Ω―Ä–Η–Φ–Β―Ä, 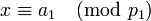 . –½–Α–Φ–Β―²–Η–Φ, ―΅―²–Ψ
. –½–Α–Φ–Β―²–Η–Φ, ―΅―²–Ψ 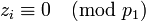 –Ω―Ä–Η
–Ω―Ä–Η 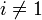 (―ç―²–Ψ –≤–Η–¥–Ϋ–Ψ –Η–Ζ –≤―΄―Ä–Α–Ε–Β–Ϋ–Η―è (1) –¥–Μ―è
(―ç―²–Ψ –≤–Η–¥–Ϋ–Ψ –Η–Ζ –≤―΄―Ä–Α–Ε–Β–Ϋ–Η―è (1) –¥–Μ―è 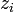 ). –Δ–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, –≤―΄―΅–Η―¹–Μ―è―è
). –Δ–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, –≤―΄―΅–Η―¹–Μ―è―è 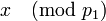 , –Ω–Ψ–Μ―É―΅–Α–Β–Φ
, –Ω–Ψ–Μ―É―΅–Α–Β–Φ 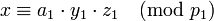 . –ù–Ψ –Η–Ζ –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―è </math>y_i</math> (2) ―¹–Μ–Β–¥―É–Β―², ―΅―²–Ψ
. –ù–Ψ –Η–Ζ –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―è </math>y_i</math> (2) ―¹–Μ–Β–¥―É–Β―², ―΅―²–Ψ 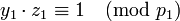 , ―²–Α–Κ ―΅―²–Ψ –Ω–Ψ–Μ―É―΅–Α–Β–Φ
, ―²–Α–Κ ―΅―²–Ψ –Ω–Ψ–Μ―É―΅–Α–Β–Φ 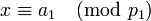 .
–Δ–Ψ –Ε–Β ―¹–Α–Φ–Ψ–Β –≤–Β―Ä–Ϋ–Ψ –¥–Μ―è –¥―Ä―É–≥–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Ι
.
–Δ–Ψ –Ε–Β ―¹–Α–Φ–Ψ–Β –≤–Β―Ä–Ϋ–Ψ –¥–Μ―è –¥―Ä―É–≥–Η―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Ι 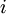 .
.
–Γ―É―â–Β―¹―²–≤–Ψ–≤–Α–Ϋ–Η–Β ―Ä–Β―à–Β–Ϋ–Η―è –¥–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ.
–î–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨―¹―²–≤–Ψ 2.
–ù–Α–Ι–¥―ë–Φ ―΅–Η―¹–Μ–Ψ 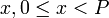 , ―É–¥–Ψ–≤–Μ–Β―²–≤–Ψ―Ä―è―é―â–Β–Β –Ψ–¥–Ϋ–Ψ–≤―Ä–Β–Φ–Β–Ϋ–Ϋ–Ψ –≤―¹–Β–Φ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è–Φ, ―É–Κ–Α–Ζ–Α–Ϋ–Ϋ―΄–Φ –≤ ―²–Β–Ψ―Ä–Β–Φ–Β. –Γ–Η―¹―²–Β–Φ―É ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι –±―É–¥–Β–Φ ―Ä–Β―à–Α―²―¨ –Ω―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ–Β–Ϋ–Η–Β–Φ –Ϋ–Α –Κ–Α–Ε–¥–Ψ–Φ ―à–Α–≥–Β –Ϋ–Ψ–≤–Ψ–≥–Ψ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è. –ü–Β―Ä–≤–Ψ–Β ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―¹–Ω―Ä–Α–≤–Β–¥–Μ–Η–≤–Ψ –¥–Μ―è –≤―¹―è–Κ–Ψ–≥–Ψ ―Ü–Β–Μ–Ψ–≥–Ψ ―΅–Η―¹–Μ–Α
, ―É–¥–Ψ–≤–Μ–Β―²–≤–Ψ―Ä―è―é―â–Β–Β –Ψ–¥–Ϋ–Ψ–≤―Ä–Β–Φ–Β–Ϋ–Ϋ–Ψ –≤―¹–Β–Φ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è–Φ, ―É–Κ–Α–Ζ–Α–Ϋ–Ϋ―΄–Φ –≤ ―²–Β–Ψ―Ä–Β–Φ–Β. –Γ–Η―¹―²–Β–Φ―É ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι –±―É–¥–Β–Φ ―Ä–Β―à–Α―²―¨ –Ω―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ–Β–Ϋ–Η–Β–Φ –Ϋ–Α –Κ–Α–Ε–¥–Ψ–Φ ―à–Α–≥–Β –Ϋ–Ψ–≤–Ψ–≥–Ψ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è. –ü–Β―Ä–≤–Ψ–Β ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―¹–Ω―Ä–Α–≤–Β–¥–Μ–Η–≤–Ψ –¥–Μ―è –≤―¹―è–Κ–Ψ–≥–Ψ ―Ü–Β–Μ–Ψ–≥–Ψ ―΅–Η―¹–Μ–Α 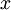 –≤–Η–¥–Α
–≤–Η–¥–Α
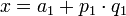 , –≥–¥–Β
, –≥–¥–Β 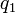 - –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ–Ψ–Β ―Ü–Β–Μ–Ψ–Β ―΅–Η―¹–Μ–Ψ.
- –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ–Ψ–Β ―Ü–Β–Μ–Ψ–Β ―΅–Η―¹–Μ–Ψ.
–î–Μ―è –Ϋ–Α―Ö–Ψ–Ε–¥–Β–Ϋ–Η―è 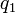 –Ω–Ψ–¥―¹―²–Α–≤–Η–Φ –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β
–Ω–Ψ–¥―¹―²–Α–≤–Η–Φ –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β 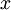 –≤–Ψ –≤―²–Ψ―Ä–Ψ–Β ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―¹–Η―¹―²–Β–Φ―΄,
–Ω–Ψ―¹–Μ–Β ―΅–Β–≥–Ψ –Ω–Ψ–Μ―É―΅–Η–Φ
–≤–Ψ –≤―²–Ψ―Ä–Ψ–Β ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―¹–Η―¹―²–Β–Φ―΄,
–Ω–Ψ―¹–Μ–Β ―΅–Β–≥–Ψ –Ω–Ψ–Μ―É―΅–Η–Φ 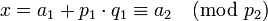 ,
–Ψ―²–Κ―É–¥–Α
,
–Ψ―²–Κ―É–¥–Α 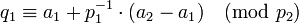 ,
,
–≥–¥–Β 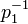 - –Ψ–±―Ä–Α―²–Ϋ―΄–Ι –Φ―É–Μ―¨―²–Η–Ω–Μ–Η–Κ–Α―²–Η–≤–Ϋ―΄–Ι ―ç–Μ–Β–Φ–Β–Ϋ―² –Κ
- –Ψ–±―Ä–Α―²–Ϋ―΄–Ι –Φ―É–Μ―¨―²–Η–Ω–Μ–Η–Κ–Α―²–Η–≤–Ϋ―΄–Ι ―ç–Μ–Β–Φ–Β–Ϋ―² –Κ 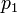 –Ω–Ψ –Φ–Ψ–¥―É–Μ―é
–Ω–Ψ –Φ–Ψ–¥―É–Μ―é 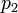 .
–Δ–Α–Κ–Ψ–Ι ―ç–Μ–Β–Φ–Β–Ϋ―² ―¹―É―â–Β―¹―²–≤―É–Β―², ―²–Α–Κ –Κ–Α–Κ
.
–Δ–Α–Κ–Ψ–Ι ―ç–Μ–Β–Φ–Β–Ϋ―² ―¹―É―â–Β―¹―²–≤―É–Β―², ―²–Α–Κ –Κ–Α–Κ 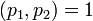 .
.
–ù–Α–Ι–¥–Β–Ϋ–Ϋ–Ψ–Β ―²–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ 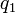 –Φ–Ψ–Ε–Ϋ–Ψ –Ζ–Α–Ω–Η―¹–Α―²―¨ –≤ –≤–Η–¥–Β
–Φ–Ψ–Ε–Ϋ–Ψ –Ζ–Α–Ω–Η―¹–Α―²―¨ –≤ –≤–Η–¥–Β
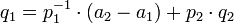
–¥–Μ―è –Ϋ–Β–Κ–Ψ―²–Ψ―Ä–Ψ–≥–Ψ ―Ü–Β–Μ–Ψ–≥–Ψ ―΅–Η―¹–Μ–Α 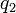 .
.
–ü–Ψ–¥―¹―²–Α–≤–Η–Φ –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β 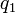 –≤ –≤―΄―Ä–Α–Ε–Β–Ϋ–Η–Β
–≤ –≤―΄―Ä–Α–Ε–Β–Ϋ–Η–Β
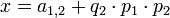 .
.
–Δ–Β–Ω–Β―Ä―¨ –Ω–Β―Ä–≤―΄–Β –¥–≤–Α ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –Φ–Ψ–≥―É―² –±―΄―²―¨ –Ζ–Α–Φ–Β–Ϋ–Β–Ϋ―΄ –Ϋ–Α –Ψ–¥–Ϋ–Ψ
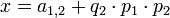 .
.
–ü―Ä–Η–Φ–Β–Ϋ–Η–Φ ―²–Β–Ω–Β―Ä―¨ –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ―É―é –Ω―Ä–Ψ―Ü–Β–¥―É―Ä―É –Κ –Ω–Ψ–Μ―É―΅–Β–Ϋ–Ϋ–Ψ–Φ―É ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η―é –Η –Κ –Ψ–¥–Ϋ–Ψ–Φ―É –Η–Ζ –Ψ―¹―²–Α–≤―à–Η―Ö―¹―è ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι –Η―¹―Ö–Ψ–¥–Ϋ–Ψ–Ι ―¹–Η―¹―²–Β–Φ―΄. –ü–Ψ–≤―²–Ψ―Ä―è―è ―ç―²–Ψ―² –Ω―Ä–Ψ―Ü–Β―¹―¹ 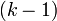 ―Ä–Α–Ζ, –Φ―΄ –≤ –Κ–Ψ–Ϋ–Β―΅–Ϋ–Ψ–Φ –Η―²–Ψ–≥–Β –Ϋ–Α–Ι–¥―ë–Φ ―΅–Η―¹–Μ–Ψ
―Ä–Α–Ζ, –Φ―΄ –≤ –Κ–Ψ–Ϋ–Β―΅–Ϋ–Ψ–Φ –Η―²–Ψ–≥–Β –Ϋ–Α–Ι–¥―ë–Φ ―΅–Η―¹–Μ–Ψ 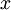 , ―É–¥–Ψ–≤–Μ–Β―²–≤–Ψ―Ä―è―é―â–Β–Β –≤―¹–Β–Φ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è–Φ –Η―¹―Ö–Ψ–¥–Ϋ–Ψ–Ι ―¹–Η―¹―²–Β–Φ―΄.
, ―É–¥–Ψ–≤–Μ–Β―²–≤–Ψ―Ä―è―é―â–Β–Β –≤―¹–Β–Φ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è–Φ –Η―¹―Ö–Ψ–¥–Ϋ–Ψ–Ι ―¹–Η―¹―²–Β–Φ―΄.
–Γ―É―â–Β―¹―²–≤–Ψ–≤–Α–Ϋ–Η–Β ―Ä–Β―à–Β–Ϋ–Η―è –¥–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ.
–î–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨―¹―²–≤–Ψ –Β–¥–Η–Ϋ―¹―²–≤–Β–Ϋ–Ϋ–Ψ―¹―²–Η.
–î–Ψ–Κ–Α–Ε–Β–Φ –Β–¥–Η–Ϋ―¹―²–≤–Β–Ϋ–Ϋ–Ψ―¹―²―¨ ―Ä–Β―à–Β–Ϋ–Η―è. –£–Ψ―¹–Ω–Ψ–Μ―¨–Ζ―É–Β–Φ―¹―è –Φ–Β―²–Ψ–¥–Ψ–Φ –Ψ―² –Ω―Ä–Ψ―²–Η–≤–Ϋ–Ψ–≥–Ψ. –ü―Ä–Β–¥–Ω–Ψ–Μ–Ψ–Ε–Η–Φ, ―΅―²–Ψ ―¹―É―â–Β―¹―²–≤―É–Β―² –¥―Ä―É–≥–Ψ–Β ―Ä–Β―à–Β–Ϋ–Η–Β 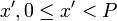 –Η―¹―Ö–Ψ–¥–Ϋ–Ψ–Ι ―¹–Η―¹―²–Β–Φ―΄.
–Η―¹―Ö–Ψ–¥–Ϋ–Ψ–Ι ―¹–Η―¹―²–Β–Φ―΄.
–Δ–Ψ–≥–¥–Α
–¥–Μ―è –≤―¹–Β―Ö 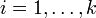 .
.
–£―΄―΅–Η―²–Α―è –Ω–Ψ―΅–Μ–Β–Ϋ–Ϋ–Ψ –Η–Ζ –Ω–Β―Ä–≤–Ψ–≥–Ψ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –≤―²–Ψ―Ä–Ψ–Β, –Ω–Ψ–Μ―É―΅–Η–Φ –Η―¹―²–Η–Ϋ–Ϋ–Ψ–Β ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β 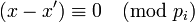 ,
–Ψ―²–Κ―É–¥–Α ―¹–Μ–Β–¥―É–Β―², ―΅―²–Ψ –¥–Μ―è –≤―¹–Β―Ö
,
–Ψ―²–Κ―É–¥–Α ―¹–Μ–Β–¥―É–Β―², ―΅―²–Ψ –¥–Μ―è –≤―¹–Β―Ö 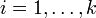
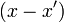 –¥–Β–Μ–Η―²―¹―è –Ϋ–Α―Ü–Β–Μ–Ψ –Ϋ–Α
–¥–Β–Μ–Η―²―¹―è –Ϋ–Α―Ü–Β–Μ–Ψ –Ϋ–Α 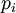 . –ù–Ψ ―²–Ψ–≥–¥–Α
. –ù–Ψ ―²–Ψ–≥–¥–Α 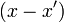 –¥–Β–Μ–Η―²―¹―è –Ϋ–Α―Ü–Β–Μ–Ψ –Ϋ–Α
–¥–Β–Μ–Η―²―¹―è –Ϋ–Α―Ü–Β–Μ–Ψ –Ϋ–Α  ,―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ,
,―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ,  , ―²–Α–Κ –Κ–Α–Κ
, ―²–Α–Κ –Κ–Α–Κ 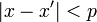 .
.
–Δ–Β–Ψ―Ä–Β–Φ–Α –¥–Ψ–Κ–Α–Ζ–Α–Ϋ–Α.