–ö–Η―²–Α–Ι―¹–Κ–Α―è ―²–Β–Ψ―Ä–Β–Φ–Α –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö
–ö–Η―²–Α–Ι―¹–Κ–Α―è ―²–Β–Ψ―Ä–Β–Φ–Α –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö ―³–Ψ―Ä–Φ―É–Μ–Η―Ä―É–Β―²―¹―è ―¹–Μ–Β–¥―É―é―â–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ:
–Δ–Β–Ψ―Ä–Β–Φ–Α.
–ü―É―¹―²―¨ 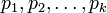 - –Ω–Ψ–Ω–Α―Ä–Ϋ–Ψ –≤–Ζ–Α–Η–Φ–Ϋ–Ψ –Ω―Ä–Ψ―¹―²―΄–Β ―΅–Η―¹–Μ–Α, –±–Ψ–Μ―¨―à–Η–Β 1, –Η –Ω―É―¹―²―¨
- –Ω–Ψ–Ω–Α―Ä–Ϋ–Ψ –≤–Ζ–Α–Η–Φ–Ϋ–Ψ –Ω―Ä–Ψ―¹―²―΄–Β ―΅–Η―¹–Μ–Α, –±–Ψ–Μ―¨―à–Η–Β 1, –Η –Ω―É―¹―²―¨ 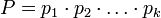 . –Δ–Ψ–≥–¥–Α ―¹―É―â–Β―¹―²–≤―É–Β―² –Β–¥–Η–Ϋ―¹―²–≤–Β–Ϋ–Ϋ–Ψ–Β –Ϋ–Β–Ψ―²―Ä–Η―Ü–Α―²–Β–Μ―¨–Ϋ–Ψ–Β ―Ä–Β―à–Β–Ϋ–Η–Β –Ω–Ψ –Φ–Ψ–¥―É–Μ―é
. –Δ–Ψ–≥–¥–Α ―¹―É―â–Β―¹―²–≤―É–Β―² –Β–¥–Η–Ϋ―¹―²–≤–Β–Ϋ–Ϋ–Ψ–Β –Ϋ–Β–Ψ―²―Ä–Η―Ü–Α―²–Β–Μ―¨–Ϋ–Ψ–Β ―Ä–Β―à–Β–Ϋ–Η–Β –Ω–Ψ –Φ–Ψ–¥―É–Μ―é 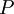 ―¹–Μ–Β–¥―É―é―â–Β–Ι ―¹–Η―¹―²–Β–Φ―΄ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι:
―¹–Μ–Β–¥―É―é―â–Β–Ι ―¹–Η―¹―²–Β–Φ―΄ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι:
-
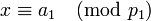 ,
,
-
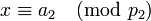 ,
,
-
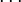 ,
,
-
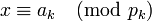 .
.
–î―Ä―É–≥–Η–Φ–Η ―¹–Μ–Ψ–≤–Α–Φ–Η, –Ψ―²–Ψ–±―Ä–Α–Ε–Β–Ϋ–Η–Β, –Κ–Ψ―²–Ψ―Ä–Ψ–Β –Κ–Α–Ε–¥–Ψ–Φ―É ―Ü–Β–Μ–Ψ–Φ―É ―΅–Η―¹–Μ―É  ,
, 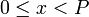 , ―¹―²–Α–≤–Η―² –≤ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Κ–Ψ―Ä―²–Β–Ε
, ―¹―²–Α–≤–Η―² –≤ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Κ–Ψ―Ä―²–Β–Ε 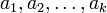 , –≥–¥–Β
, –≥–¥–Β 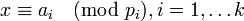 ―è–≤–Μ―è–Β―²―¹―è –±–Η–Β–Κ―Ü–Η–Β–Ι –Κ–Ψ–Μ―¨―Ü–Α
―è–≤–Μ―è–Β―²―¹―è –±–Η–Β–Κ―Ü–Η–Β–Ι –Κ–Ψ–Μ―¨―Ü–Α 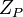 –Ϋ–Α –¥–Β–Κ–Α―Ä―²–Ψ–≤–Ψ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β
–Ϋ–Α –¥–Β–Κ–Α―Ä―²–Ψ–≤–Ψ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β 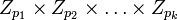 –Κ–Ψ–Μ–Β―Ü
–Κ–Ψ–Μ–Β―Ü 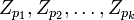 .
.
–Δ.–Β. ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Φ–Β–Ε–¥―É ―΅–Η―¹–Μ–Α–Φ–Η –Η –Κ–Ψ―Ä―²–Β–Ε–Α–Φ–Η ―è–≤–Μ―è–Β―²―¹―è –≤–Ζ–Α–Η–Φ–Ϋ–Ψ –Ψ–¥–Ϋ–Ψ–Ζ–Ϋ–Α―΅–Ϋ―΄–Φ, –Κ―Ä–Ψ–Φ–Β ―²–Ψ–≥–Ψ, –Ψ–Ω–Β―Ä–Α―Ü–Η–Η, –≤―΄–Ω–Ψ–Μ–Ϋ―è–Β–Φ―΄–Β –Ϋ–Α–¥ ―΅–Η―¹–Μ–Ψ–Φ  , –Φ–Ψ–Ε–Ϋ–Ψ ―ç–Κ–≤–Η–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ –≤―΄–Ω–Ψ–Μ–Ϋ―è―²―¨ –Ϋ–Α–¥ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤―É―é―â–Η–Φ–Η ―ç–Μ–Β–Φ–Β–Ϋ―²–Α–Φ–Η –Κ–Ψ―Ä―²–Β–Ε–Α–Φ–Η –Ω―É―²―ë–Φ –Ϋ–Β–Ζ–Α–≤–Η―¹–Η–Φ–Ψ–≥–Ψ –≤―΄–Ω–Ψ–Μ–Ϋ–Β–Ϋ–Η―è –Ψ–Ω–Β―Ä–Α―Ü–Η–Ι –Ϋ–Α–¥ –Κ–Α–Ε–¥―΄–Φ –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²–Ψ–Φ:
, –Φ–Ψ–Ε–Ϋ–Ψ ―ç–Κ–≤–Η–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ –≤―΄–Ω–Ψ–Μ–Ϋ―è―²―¨ –Ϋ–Α–¥ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤―É―é―â–Η–Φ–Η ―ç–Μ–Β–Φ–Β–Ϋ―²–Α–Φ–Η –Κ–Ψ―Ä―²–Β–Ε–Α–Φ–Η –Ω―É―²―ë–Φ –Ϋ–Β–Ζ–Α–≤–Η―¹–Η–Φ–Ψ–≥–Ψ –≤―΄–Ω–Ψ–Μ–Ϋ–Β–Ϋ–Η―è –Ψ–Ω–Β―Ä–Α―Ü–Η–Ι –Ϋ–Α–¥ –Κ–Α–Ε–¥―΄–Φ –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²–Ψ–Φ:
–Β―¹–Μ–Η
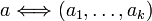 ,
,
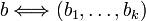 ,
,
―²–Ψ ―¹–Ω―Ä–Α–≤–Β–¥–Μ–Η–≤–Ψ:
-
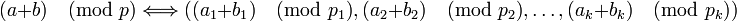 ,
,
-
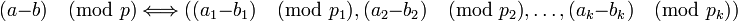 ,
,
-
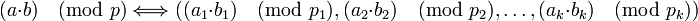 .
.
–Γ―É―â–Β―¹―²–≤―É–Β―² –Φ–Ϋ–Ψ–≥–Ψ ―Ä–Α–Ζ–Μ–Η―΅–Ϋ―΄―Ö –¥–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨―¹―²–≤ –Κ–Η―²–Α–Ι―¹–Κ–Ψ–Ι ―²–Β–Ψ―Ä–Β–Φ―΄ –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö. –ü―Ä–Η–≤–Β–¥―ë–Φ –Κ–Ψ–Ϋ―¹―²―Ä―É–Κ―²–Η–≤–Ϋ–Ψ–Β –¥–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨―¹―²–≤–Ψ ―ç―²–Ψ–Ι ―²–Β–Ψ―Ä–Β–Φ―΄.