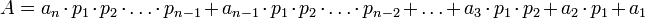Перевод числа из СОК в обобщенную позиционную систему
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
Рассмотрим метод определения величины числа связанный с переводом числа из системы остаточных классов в обобщенную позиционную систему (ОПС). Для этого выявим связь между представлением некоторого числа в этих двух системах. | Рассмотрим метод определения величины числа связанный с переводом числа из системы остаточных классов в обобщенную позиционную систему (ОПС). Для этого выявим связь между представлением некоторого числа в этих двух системах. | ||
| + | |||
| + | |||
| + | '''Алгоритм перевода числа из СОК в обобщенную позиционную систему''' | ||
Пусть СОК задается основаниями <math>p_1, p_2, \ldots, p_n</math> и <math>A = ({\alpha}_1, {\alpha}_2, \ldots, {\alpha}_n)</math> - число в этой системе. И пусть <math>p_1, p_2, \ldots, p_n</math> являются также основаниями ОПС, тогда число <math>A</math> можно представить в виде | Пусть СОК задается основаниями <math>p_1, p_2, \ldots, p_n</math> и <math>A = ({\alpha}_1, {\alpha}_2, \ldots, {\alpha}_n)</math> - число в этой системе. И пусть <math>p_1, p_2, \ldots, p_n</math> являются также основаниями ОПС, тогда число <math>A</math> можно представить в виде | ||
| Строка 42: | Строка 45: | ||
Перевод, осуществляемый согласно описанному алгоритму,содержит всего <math>2 \cdot (n-1)</math> остаточных арифметических операций вычитания и деления без остатка, где <math>n</math> – число модулей системы. | Перевод, осуществляемый согласно описанному алгоритму,содержит всего <math>2 \cdot (n-1)</math> остаточных арифметических операций вычитания и деления без остатка, где <math>n</math> – число модулей системы. | ||
| + | |||
| + | '''Модификация алгоритма перевода числа из СОК в обобщенную позиционную систему''' | ||
| + | |||
| + | Можно предложить некоторую модификацию алгоритма с заменой операции деления операцией умножения. Для этого предварительно вычисляется <math>\frac{n\cdot (n-1)}{2}</math> констант <math>\tau_{k,j}</math>, которые удовлетворяют условию | ||
| + | |||
| + | :<math>\tau_{k,j}\cdot p_k \equiv 1\pmod p_j, 1 \le k < j \le n</math>. | ||
| + | |||
| + | Эти константы можно, например получить из расширенного алгоритма Евклида | ||
| + | |||
| + | :<math>\tau_{k,j}\cdot p_k + \gamma \cdot p_j = HOD (p_k, p_j) = 1</math>. | ||
| + | |||
| + | Здесь следует заметить тот факт, что константы полностью определяются выбранной системой оснований, поэтому могут быть вычислены заранее и храниться в некоторой таблице. | ||
| + | |||
| + | Если константы <math>\tau_{k,j}</math> вычислены, то вычисление цифр <math>a_i</math> ОПС по модифицированному алгоритму может быть переписано в виде: | ||
| + | |||
| + | <math>a_1 \equiv {\alpha}_1 \pmod p_1</math>, | ||
| + | |||
| + | <math>a_2 \equiv ({\alpha}_2 - {\alpha}_1) \cdot \tau_{1,2} \pmod p_2</math>, | ||
| + | |||
| + | <math>a_3 \equiv (({\alpha}_3 - {\alpha}_1) \cdot \tau_{1,3} - {\alpha}_2) \tau_{2,3} \pmod p_3</math>, | ||
| + | |||
| + | <math>\ldots</math> | ||
| + | |||
| + | <math>a_n \equiv (\ldots (({\alpha}_n - {\alpha}_1) \cdot \tau_{1,n} - {\alpha}_2) \tau_{2,n} - \ldots {\alpha}_{n-1} \cdot \tau_{n-1,n} \pmod p_n</math>. | ||
| + | |||
| + | Константы <math>\tau_{k,j}</math> принято также записывать в виде <math>\tau_{k,j} = \left | \right | \pmod </math> и называть обратными элементами по умножению для чисел по модулю (multiplicative inverse). | ||
Версия 15:29, 15 октября 2014
Рассмотрим метод определения величины числа связанный с переводом числа из системы остаточных классов в обобщенную позиционную систему (ОПС). Для этого выявим связь между представлением некоторого числа в этих двух системах.
Алгоритм перевода числа из СОК в обобщенную позиционную систему
Пусть СОК задается основаниями 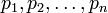 и
и 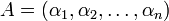 - число в этой системе. И пусть
- число в этой системе. И пусть 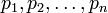 являются также основаниями ОПС, тогда число
являются также основаниями ОПС, тогда число  можно представить в виде
можно представить в виде
где 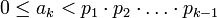 – коэффициенты (цифры) ОПС.
– коэффициенты (цифры) ОПС.
Очевидно, что диапазоны чисел, представимых в СОК и ОПС совпадают, т.е. можно говорить о наличии взаимно однозначного соответствия между множеством представлений чисел в СОК и ОПС.
Предыдущее равенство можно переписать в следующем виде:
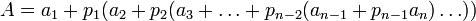 ,
,
откуда следует, что цифры ОПС могут быть получены из соотношений:
![a_1 = A - \left[ \frac{A}{p_1}\right] \cdot p_1 = A - A_1\cdot p_1](/w/images/math/5/0/a/50a6fc0ade7777bdc4d8d35ac5bf0fdc.png) , где
, где ![A_1 = \left[ \frac{A}{p_1}\right]](/w/images/math/4/3/1/431a38d08bce70f125650a3bb0f990ab.png) ,
,
![a_2 = A_1 - \left[ \frac{A_1}{p_2}\right] \cdot p_2 = A_1 - A_2\cdot p_2](/w/images/math/0/0/7/007d1b08c85bdb3b0a9090942d8da1ee.png) , где
, где ![A_2 = \left[ \frac{A_1}{p_2}\right]](/w/images/math/e/d/2/ed27b2acb3c3345e4b972add08027141.png) ,
,
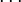
![a_n = A_{n-1} - \left[ \frac{A_{n-1}}{p_n}\right] \cdot p_n = A_{n-1} - A_n\cdot p_n](/w/images/math/1/b/c/1bc8ed50002267d059a3fefc62fd07a1.png) , где
, где ![A_n = \left[ \frac{A_{n-1}}{p_n}\right]](/w/images/math/b/7/c/b7cdc8251bbd63614e6e91f2b59da5dd.png) .
.
Причем при определении цифр 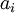 по этим формулам все вычисления можно вести в СОК.
по этим формулам все вычисления можно вести в СОК.
Действительно, из формул следует, что 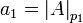 , т.е.
, т.е. 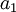 - первая СОК цифра, или
- первая СОК цифра, или 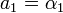 .
Для получения
.
Для получения 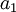 сперва представим
сперва представим 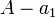 в остаточном коде. Очевидно, что
в остаточном коде. Очевидно, что 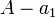 делится на
делится на 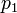 . Более того,
. Более того, 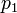 взаимно просто со всеми другими модулями. Следовательно, для нахождения цифры
взаимно просто со всеми другими модулями. Следовательно, для нахождения цифры 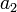 может быть использована процедура деления без остатка:
может быть использована процедура деления без остатка:
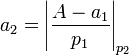 .
.
Таким путем, с помощью вычитаний и делений в остаточной записи все цифры ОПС могут быть получены. При этом замечено, что
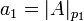 ,
, ![a_2 = \left|\left[\frac{A}{p_1}\right]\right|_{p_2}](/w/images/math/6/6/3/6632a5ad0ce1ea59f81c11b77a7d9b0f.png) ,
, ![a_3 = \left|\left[\frac{A}{p_1\cdot p_2}\right]\right|_{p_3}](/w/images/math/0/8/a/08a8191963671a486258fc188fa05f47.png)
и, вообще, для 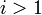
![a_i = \left|\left[\frac{A}{p_1\cdot p_2 \cdot \ldots \cdot p_{i-1}}\right]\right|_{p_i}](/w/images/math/7/1/8/718edb3aef301739d1dc94f50d11c3c1.png) .
.
Перевод, осуществляемый согласно описанному алгоритму,содержит всего 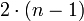 остаточных арифметических операций вычитания и деления без остатка, где
остаточных арифметических операций вычитания и деления без остатка, где  – число модулей системы.
– число модулей системы.
Модификация алгоритма перевода числа из СОК в обобщенную позиционную систему
Можно предложить некоторую модификацию алгоритма с заменой операции деления операцией умножения. Для этого предварительно вычисляется 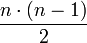 констант
констант 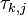 , которые удовлетворяют условию
, которые удовлетворяют условию
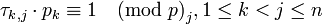 .
.
Эти константы можно, например получить из расширенного алгоритма Евклида
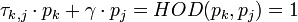 .
.
Здесь следует заметить тот факт, что константы полностью определяются выбранной системой оснований, поэтому могут быть вычислены заранее и храниться в некоторой таблице.
Если константы 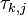 вычислены, то вычисление цифр
вычислены, то вычисление цифр 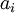 ОПС по модифицированному алгоритму может быть переписано в виде:
ОПС по модифицированному алгоритму может быть переписано в виде:
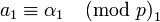 ,
,
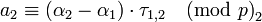 ,
,
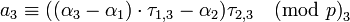 ,
,
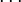
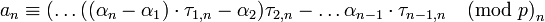 .
.
Константы 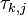 принято также записывать в виде Невозможно разобрать выражение (синтаксическая ошибка): \tau_{k,j} = \left | \right | \pmod
принято также записывать в виде Невозможно разобрать выражение (синтаксическая ошибка): \tau_{k,j} = \left | \right | \pmod
и называть обратными элементами по умножению для чисел по модулю (multiplicative inverse).