–Γ–Η―¹―²–Β–Φ–Α –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤
| –Γ―²―Ä–Ψ–Κ–Α 1: | –Γ―²―Ä–Ψ–Κ–Α 1: | ||
'''–Γ–Η―¹―²–Β–Φ–Α –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ (–Γ–û–ö)''' (–Ψ―² –Α–Ϋ–≥–Μ. [http://en.wikipedia.org/wiki/Residue_number_system Residue number system], –¥―Ä―É–≥–Ψ–Β –Ϋ–Α–Ζ–≤–Α–Ϋ–Η–Β '''–€–Ψ–¥―É–Μ―è―Ä–Ϋ–Α―è –Α―Ä–Η―³–Φ–Β―²–Η–Κ–Α''') - [http://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F#.D0.9D.D0.B5.D0.BF.D0.BE.D0.B7.D0.B8.D1.86.D0.B8.D0.BE.D0.BD.D0.BD.D1.8B.D0.B5_.D1.81.D0.B8.D1.81.D1.82.D0.B5.D0.BC.D1.8B_.D1.81.D1.87.D0.B8.D1.81.D0.BB.D0.B5.D0.BD.D0.B8.D1.8F –Ϋ–Β–Ω–Ψ–Ζ–Η―Ü–Η–Ψ–Ϋ–Ϋ–Α―è ―¹–Η―¹―²–Β–Φ–Α ―¹―΅–Η―¹–Μ–Β–Ϋ–Η―è]. –ü―Ä–Β–¥―¹―²–Α–≤–Μ–Β–Ϋ–Η–Β ―΅–Η―¹–Μ–Α –≤ ―¹–Η―¹―²–Β–Φ–Β –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Ψ –Ϋ–Α –Ω–Ψ–Ϋ―è―²–Η–Η [http://ru.wikipedia.org/wiki/%D0%A1%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BF%D0%BE_%D0%BC%D0%BE%D0%B4%D1%83%D0%BB%D1%8E –≤―΄―΅–Β―²–Α] –Η [http://ru.wikipedia.org/wiki/%D0%9A%D0%B8%D1%82%D0%B0%D0%B9%D1%81%D0%BA%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%BE%D0%B1_%D0%BE%D1%81%D1%82%D0%B0%D1%82%D0%BA%D0%B0%D1%85 –Κ–Η―²–Α–Ι―¹–Κ–Ψ–Ι ―²–Β–Ψ―Ä–Β–Φ–Β –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö]. –Γ–û–ö –Ψ–Ω―Ä–Β–¥–Β–Μ―è–Β―²―¹―è –Ϋ–Α–±–Ψ―Ä–Ψ–Φ [http://ru.wikipedia.org/wiki/%D0%92%D0%B7%D0%B0%D0%B8%D0%BC%D0%BD%D0%BE_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%8B%D0%B5_%D1%87%D0%B8%D1%81%D0%BB%D0%B0 –≤–Ζ–Α–Η–Φ–Ϋ–Ψ –Ω―Ä–Ψ―¹―²―΄―Ö] ''–Φ–Ψ–¥―É–Μ–Β–Ι'' <math>(m_1, m_2, \dots, m_n)</math> ―¹ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β–Φ <math>M=m_1\cdot m_2\cdot \dots\cdot m_n</math> ―²–Α–Κ, ―΅―²–Ψ –Κ–Α–Ε–¥–Ψ–Φ―É ―Ü–Β–Μ–Ψ–Φ―É ―΅–Η―¹–Μ―É <math>x</math> –Η–Ζ –Ψ―²―Ä–Β–Ζ–Κ–Α <math>[0,M-1]</math> ―¹―²–Α–≤–Η―²―¹―è –≤ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Ϋ–Α–±–Ψ―Ä –≤―΄―΅–Β―²–Ψ–≤ <math>(x_1, x_2, \dots, x_n)</math>, –≥–¥–Β | '''–Γ–Η―¹―²–Β–Φ–Α –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ (–Γ–û–ö)''' (–Ψ―² –Α–Ϋ–≥–Μ. [http://en.wikipedia.org/wiki/Residue_number_system Residue number system], –¥―Ä―É–≥–Ψ–Β –Ϋ–Α–Ζ–≤–Α–Ϋ–Η–Β '''–€–Ψ–¥―É–Μ―è―Ä–Ϋ–Α―è –Α―Ä–Η―³–Φ–Β―²–Η–Κ–Α''') - [http://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F#.D0.9D.D0.B5.D0.BF.D0.BE.D0.B7.D0.B8.D1.86.D0.B8.D0.BE.D0.BD.D0.BD.D1.8B.D0.B5_.D1.81.D0.B8.D1.81.D1.82.D0.B5.D0.BC.D1.8B_.D1.81.D1.87.D0.B8.D1.81.D0.BB.D0.B5.D0.BD.D0.B8.D1.8F –Ϋ–Β–Ω–Ψ–Ζ–Η―Ü–Η–Ψ–Ϋ–Ϋ–Α―è ―¹–Η―¹―²–Β–Φ–Α ―¹―΅–Η―¹–Μ–Β–Ϋ–Η―è]. –ü―Ä–Β–¥―¹―²–Α–≤–Μ–Β–Ϋ–Η–Β ―΅–Η―¹–Μ–Α –≤ ―¹–Η―¹―²–Β–Φ–Β –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Ψ –Ϋ–Α –Ω–Ψ–Ϋ―è―²–Η–Η [http://ru.wikipedia.org/wiki/%D0%A1%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BF%D0%BE_%D0%BC%D0%BE%D0%B4%D1%83%D0%BB%D1%8E –≤―΄―΅–Β―²–Α] –Η [http://ru.wikipedia.org/wiki/%D0%9A%D0%B8%D1%82%D0%B0%D0%B9%D1%81%D0%BA%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%BE%D0%B1_%D0%BE%D1%81%D1%82%D0%B0%D1%82%D0%BA%D0%B0%D1%85 –Κ–Η―²–Α–Ι―¹–Κ–Ψ–Ι ―²–Β–Ψ―Ä–Β–Φ–Β –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö]. –Γ–û–ö –Ψ–Ω―Ä–Β–¥–Β–Μ―è–Β―²―¹―è –Ϋ–Α–±–Ψ―Ä–Ψ–Φ [http://ru.wikipedia.org/wiki/%D0%92%D0%B7%D0%B0%D0%B8%D0%BC%D0%BD%D0%BE_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%8B%D0%B5_%D1%87%D0%B8%D1%81%D0%BB%D0%B0 –≤–Ζ–Α–Η–Φ–Ϋ–Ψ –Ω―Ä–Ψ―¹―²―΄―Ö] ''–Φ–Ψ–¥―É–Μ–Β–Ι'' <math>(m_1, m_2, \dots, m_n)</math> ―¹ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β–Φ <math>M=m_1\cdot m_2\cdot \dots\cdot m_n</math> ―²–Α–Κ, ―΅―²–Ψ –Κ–Α–Ε–¥–Ψ–Φ―É ―Ü–Β–Μ–Ψ–Φ―É ―΅–Η―¹–Μ―É <math>x</math> –Η–Ζ –Ψ―²―Ä–Β–Ζ–Κ–Α <math>[0,M-1]</math> ―¹―²–Α–≤–Η―²―¹―è –≤ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Ϋ–Α–±–Ψ―Ä –≤―΄―΅–Β―²–Ψ–≤ <math>(x_1, x_2, \dots, x_n)</math>, –≥–¥–Β | ||
| β࣠| : <math> | + | : <math>x_1 \equiv x \pmod{m_1};</math> |
| β࣠| : <math> | + | : <math>x_2 \equiv x \pmod{m_2};</math> |
: βÄΠ | : βÄΠ | ||
| β࣠| : <math> | + | : <math>x_n \equiv x \pmod{m_n}.</math> |
–ü―Ä–Η ―ç―²–Ψ–Φ –Κ–Η―²–Α–Ι―¹–Κ–Α―è ―²–Β–Ψ―Ä–Β–Φ–Α –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö –≥–Α―Ä–Α–Ϋ―²–Η―Ä―É–Β―² –Ψ–¥–Ϋ–Ψ–Ζ–Ϋ–Α―΅–Ϋ–Ψ―¹―²―¨ –Ω―Ä–Β–¥―¹―²–Α–≤–Μ–Β–Ϋ–Η―è –¥–Μ―è ―΅–Η―¹–Β–Μ –Η–Ζ –Ψ―²―Ä–Β–Ζ–Κ–Α <math>[0,M-1]</math>. | –ü―Ä–Η ―ç―²–Ψ–Φ –Κ–Η―²–Α–Ι―¹–Κ–Α―è ―²–Β–Ψ―Ä–Β–Φ–Α –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö –≥–Α―Ä–Α–Ϋ―²–Η―Ä―É–Β―² –Ψ–¥–Ϋ–Ψ–Ζ–Ϋ–Α―΅–Ϋ–Ψ―¹―²―¨ –Ω―Ä–Β–¥―¹―²–Α–≤–Μ–Β–Ϋ–Η―è –¥–Μ―è ―΅–Η―¹–Β–Μ –Η–Ζ –Ψ―²―Ä–Β–Ζ–Κ–Α <math>[0,M-1]</math>. | ||
–£–Β―Ä―¹–Η―è 10:29, 4 ―³–Β–≤―Ä–Α–Μ―è 2013
–Γ–Η―¹―²–Β–Φ–Α –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ (–Γ–û–ö) (–Ψ―² –Α–Ϋ–≥–Μ. Residue number system, –¥―Ä―É–≥–Ψ–Β –Ϋ–Α–Ζ–≤–Α–Ϋ–Η–Β –€–Ψ–¥―É–Μ―è―Ä–Ϋ–Α―è –Α―Ä–Η―³–Φ–Β―²–Η–Κ–Α) - –Ϋ–Β–Ω–Ψ–Ζ–Η―Ü–Η–Ψ–Ϋ–Ϋ–Α―è ―¹–Η―¹―²–Β–Φ–Α ―¹―΅–Η―¹–Μ–Β–Ϋ–Η―è. –ü―Ä–Β–¥―¹―²–Α–≤–Μ–Β–Ϋ–Η–Β ―΅–Η―¹–Μ–Α –≤ ―¹–Η―¹―²–Β–Φ–Β –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Ψ –Ϋ–Α –Ω–Ψ–Ϋ―è―²–Η–Η –≤―΄―΅–Β―²–Α –Η –Κ–Η―²–Α–Ι―¹–Κ–Ψ–Ι ―²–Β–Ψ―Ä–Β–Φ–Β –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö. –Γ–û–ö –Ψ–Ω―Ä–Β–¥–Β–Μ―è–Β―²―¹―è –Ϋ–Α–±–Ψ―Ä–Ψ–Φ –≤–Ζ–Α–Η–Φ–Ϋ–Ψ –Ω―Ä–Ψ―¹―²―΄―Ö –Φ–Ψ–¥―É–Μ–Β–Ι 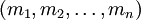 ―¹ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β–Φ
―¹ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β–Φ 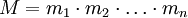 ―²–Α–Κ, ―΅―²–Ψ –Κ–Α–Ε–¥–Ψ–Φ―É ―Ü–Β–Μ–Ψ–Φ―É ―΅–Η―¹–Μ―É
―²–Α–Κ, ―΅―²–Ψ –Κ–Α–Ε–¥–Ψ–Φ―É ―Ü–Β–Μ–Ψ–Φ―É ―΅–Η―¹–Μ―É  –Η–Ζ –Ψ―²―Ä–Β–Ζ–Κ–Α
–Η–Ζ –Ψ―²―Ä–Β–Ζ–Κ–Α ![[0,M-1]](/w/images/math/5/6/5/56591240ff770cb9db7f3205c6befa98.png) ―¹―²–Α–≤–Η―²―¹―è –≤ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Ϋ–Α–±–Ψ―Ä –≤―΄―΅–Β―²–Ψ–≤
―¹―²–Α–≤–Η―²―¹―è –≤ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Ϋ–Α–±–Ψ―Ä –≤―΄―΅–Β―²–Ψ–≤ 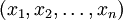 , –≥–¥–Β
, –≥–¥–Β
-
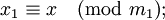
-
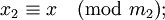
- βÄΠ
-
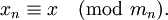
–ü―Ä–Η ―ç―²–Ψ–Φ –Κ–Η―²–Α–Ι―¹–Κ–Α―è ―²–Β–Ψ―Ä–Β–Φ–Α –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö –≥–Α―Ä–Α–Ϋ―²–Η―Ä―É–Β―² –Ψ–¥–Ϋ–Ψ–Ζ–Ϋ–Α―΅–Ϋ–Ψ―¹―²―¨ –Ω―Ä–Β–¥―¹―²–Α–≤–Μ–Β–Ϋ–Η―è –¥–Μ―è ―΅–Η―¹–Β–Μ –Η–Ζ –Ψ―²―Ä–Β–Ζ–Κ–Α ![[0,M-1]](/w/images/math/5/6/5/56591240ff770cb9db7f3205c6befa98.png) .
.
–ü―Ä–Β–Η–Φ―É―â–Β―¹―²–≤–Α ―¹–Η―¹―²–Β–Φ―΄ –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤
- –£ –Γ–û–ö –Α―Ä–Η―³–Φ–Β―²–Η―΅–Β―¹–Κ–Η–Β –Ψ–Ω–Β―Ä–Α―Ü–Η–Η (―¹–Μ–Ψ–Ε–Β–Ϋ–Η–Β, –≤―΄―΅–Η―²–Α–Ϋ–Η–Β, ―É–Φ–Ϋ–Ψ–Ε–Β–Ϋ–Η–Β, –¥–Β–Μ–Β–Ϋ–Η–Β) –≤―΄–Ω–Ψ–Μ–Ϋ―è―é―²―¹―è –Ω–Ψ–Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²–Ϋ–Ψ, –Β―¹–Μ–Η –Ω―Ä–Ψ ―Ä–Β–Ζ―É–Μ―¨―²–Α―² –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ –Ψ–Ϋ ―è–≤–Μ―è–Β―²―¹―è ―Ü–Β–Μ–Ψ―΅–Η―¹–Μ–Β–Ϋ–Ϋ―΄–Φ –Η ―²–Α–Κ–Ε–Β –Μ–Β–Ε–Η―² –≤
![[0,M-1]](/w/images/math/5/6/5/56591240ff770cb9db7f3205c6befa98.png) .
.
–ù–Β–¥–Ψ―¹―²–Α―²–Κ–Η ―¹–Η―¹―²–Β–Φ―΄ –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤
- –£–Ψ–Ζ–Φ–Ψ–Ε–Ϋ–Ψ―¹―²―¨ –Ω―Ä–Β–¥―¹―²–Α–≤–Μ–Β–Ϋ–Η―è ―²–Ψ–Μ―¨–Κ–Ψ –Ψ–≥―Ä–Α–Ϋ–Η―΅–Β–Ϋ–Ϋ–Ψ–≥–Ψ –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Α ―΅–Η―¹–Β–Μ.
- –û―²―¹―É―²―¹―²–≤–Η–Β ―ç―³―³–Β–Κ―²–Η–≤–Ϋ―΄―Ö –Α–Μ–≥–Ψ―Ä–Η―²–Φ–Ψ–≤ –¥–Μ―è ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è ―΅–Η―¹–Β–Μ, –Ω―Ä–Β–¥―¹―²–Α–≤–Μ–Β–Ϋ–Ϋ―΄―Ö –≤ –Γ–û–ö. –Γ―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ψ–±―΄―΅–Ϋ–Ψ –Ψ―¹―É―â–Β―¹―²–≤–Μ―è–Β―²―¹―è ―΅–Β―Ä–Β–Ζ –Ω–Β―Ä–Β–≤–Ψ–¥ –Α―Ä–≥―É–Φ–Β–Ϋ―²–Ψ–≤ –Η–Ζ –Γ–û–ö –≤ ―¹–Φ–Β―à–Α–Ϋ–Ϋ―É―é ―¹–Η―¹―²–Β–Φ―É ―¹―΅–Η―¹–Μ–Β–Ϋ–Η―è –Ω–Ψ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è–Φ
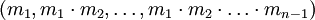 .
.
- –Γ–Μ–Ψ–Ε–Ϋ―΄–Β ―Ä–Β–Α–Μ–Η–Ζ–Α―Ü–Η–Η –Α–Μ–≥–Ψ―Ä–Η―²–Φ–Ψ–≤ –Ω–Β―Ä–Β–≤–Ψ–¥–Α –Η–Ζ –Ω–Ψ–Ζ–Η―Ü–Η–Ψ–Ϋ–Ϋ–Ψ–Ι ―¹–Η―¹―²–Β–Φ―΄ ―¹―΅–Η―¹–Μ–Β–Ϋ–Η―è –≤ –Γ–û–ö –Η –Ψ–±―Ä–Α―²–Ϋ–Ψ.
–ü―Ä–Η–Φ–Β–Ϋ–Β–Ϋ–Η–Β ―¹–Η―¹―²–Β–Φ―΄ –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤
–Γ–û–ö ―à–Η―Ä–Ψ–Κ–Ψ –Η―¹–Ω–Ψ–Μ―¨–Ζ―É–Β―²―¹―è –≤ –Φ–Η–Κ―Ä–Ψ―ç–Μ–Β–Κ―²―Ä–Ψ–Ϋ–Η–Κ–Β –≤ ―¹–Ω–Β―Ü–Η–Α–Μ–Η–Ζ–Η―Ä–Ψ–≤–Α–Ϋ–Ϋ―΄―Ö ―É―¹―²―Ä–Ψ–Ι―¹―²–≤–Α―Ö [–Π–û–Γ], –≥–¥–Β ―²―Ä–Β–±―É–Β―²―¹―è:
- –Κ–Ψ–Ϋ―²―Ä–Ψ–Μ―¨ –Ζ–Α –Ψ―à–Η–±–Κ–Α–Φ–Η, –Ζ–Α ―¹―΅–Β―² –≤–≤–Β–¥–Β–Ϋ–Η―è –¥–Ψ–Ω–Ψ–Μ–Ϋ–Η―²–Β–Μ―¨–Ϋ―΄―Ö –Η–Ζ–±―΄―²–Ψ―΅–Ϋ―΄―Ö –Φ–Ψ–¥―É–Μ–Β–Ι
- –≤―΄―¹–Ψ–Κ–Α―è ―¹–Κ–Ψ―Ä–Ψ―¹―²―¨ ―Ä–Α–±–Ψ―²―΄, –Κ–Ψ―²–Ψ―Ä―É―é –Ψ–±–Β―¹–Ω–Β―΅–Η–≤–Α–Β―² –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α―è ―Ä–Β–Α–Μ–Η–Ζ–Α―Ü–Η―è –±–Α–Ζ–Ψ–≤―΄―Ö –Α―Ä–Η―³–Φ–Β―²–Η―΅–Β―¹–Κ–Η―Ö –Ψ–Ω–Β―Ä–Α―Ü–Η–Ι
–û―¹–Ϋ–Ψ–≤–Ϋ―΄–Β –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―è
–Γ–Η―¹―²–Β–Φ–Α –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Η―¹–Ω–Ψ–Μ―¨–Ζ―É–Β―²―¹―è –¥–Μ―è –Ω―Ä–Β–¥―¹―²–Α–≤–Μ–Β–Ϋ–Η―è –±–Ψ–Μ―¨―à–Η―Ö ―΅–Η―¹–Β–Μ 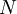 , –Ψ–±–Β―¹–Ω–Β―΅–Η–≤–Α―è ―²–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ –±–Ψ–Μ–Β–Β ―ç―³―³–Β–Κ―²–Η–≤–Ϋ―΄–Β –≤―΄―΅–Η―¹–Μ–Β–Ϋ–Η―è. –£ –Ψ―¹–Ϋ–Ψ–≤–Β –¥–Α–Ϋ–Ϋ–Ψ–≥–Ψ –Ω―Ä–Β–¥―¹―²–Α–≤–Μ–Β–Ϋ–Η―è –Μ–Β–Ε–Η―² –Η–Ζ–Ψ–Φ–Ψ―Ä―³–Η–Ζ–Φ
, –Ψ–±–Β―¹–Ω–Β―΅–Η–≤–Α―è ―²–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ –±–Ψ–Μ–Β–Β ―ç―³―³–Β–Κ―²–Η–≤–Ϋ―΄–Β –≤―΄―΅–Η―¹–Μ–Β–Ϋ–Η―è. –£ –Ψ―¹–Ϋ–Ψ–≤–Β –¥–Α–Ϋ–Ϋ–Ψ–≥–Ψ –Ω―Ä–Β–¥―¹―²–Α–≤–Μ–Β–Ϋ–Η―è –Μ–Β–Ε–Η―² –Η–Ζ–Ψ–Φ–Ψ―Ä―³–Η–Ζ–Φ 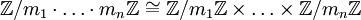 , –Κ–Ψ―²–Ψ―Ä―΄–Ι –¥–Ψ―¹―²–Α–≤–Μ―è–Β―² –Κ–Η―²–Α–Ι―¹–Κ–Α―è ―²–Β–Ψ―Ä–Β–Φ–Α –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö.
, –Κ–Ψ―²–Ψ―Ä―΄–Ι –¥–Ψ―¹―²–Α–≤–Μ―è–Β―² –Κ–Η―²–Α–Ι―¹–Κ–Α―è ―²–Β–Ψ―Ä–Β–Φ–Α –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö.
–Γ–Η―¹―²–Β–Φ–Ψ–Ι –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Ϋ–Α–Ζ―΄–≤–Α―é―² –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ–Ψ–Β –Κ–Ψ–Ϋ–Β―΅–Ϋ–Ψ–Β –Φ–Ϋ–Ψ–Ε–Β―¹―²–≤–Ψ 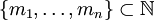 , ―²–Α–Κ–Ψ–Β ―΅―²–Ψ
, ―²–Α–Κ–Ψ–Β ―΅―²–Ψ 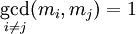 , –≥–¥–Β
, –≥–¥–Β 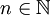 . –ü―É―¹―²―¨ –Ζ–Α–¥–Α–Ϋ–Α –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ–Α―è ―¹–Η―¹―²–Β–Φ–Α –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤
. –ü―É―¹―²―¨ –Ζ–Α–¥–Α–Ϋ–Α –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ–Α―è ―¹–Η―¹―²–Β–Φ–Α –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ 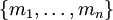 –Η –Ω–Ψ–Μ–Ψ–Ε–Η–Φ, ―΅―²–Ψ
–Η –Ω–Ψ–Μ–Ψ–Ε–Η–Φ, ―΅―²–Ψ 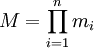 . –Δ–Ψ–≥–¥–Α –≤ ―¹–Η–Μ―É –Κ–Η―²–Α–Ι―¹–Κ–Ψ–Ι ―²–Β–Ψ―Ä–Β–Φ―΄ –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö –Η–Φ–Β–Β–Φ ―ç–Ω–Η–Φ–Ψ―Ä―³–Η–Ζ–Φ –Κ–Ψ–Μ–Β―Ü
. –Δ–Ψ–≥–¥–Α –≤ ―¹–Η–Μ―É –Κ–Η―²–Α–Ι―¹–Κ–Ψ–Ι ―²–Β–Ψ―Ä–Β–Φ―΄ –Ψ–± –Ψ―¹―²–Α―²–Κ–Α―Ö –Η–Φ–Β–Β–Φ ―ç–Ω–Η–Φ–Ψ―Ä―³–Η–Ζ–Φ –Κ–Ψ–Μ–Β―Ü 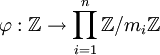 , ―².―΅.
, ―².―΅. 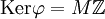 , –Κ–Ψ―²–Ψ―Ä―΄–Ι –Η–Ϋ–¥―É―Ü–Η―Ä―É–Β―² –Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Η–Ι –Η–Ζ–Ψ–Φ–Ψ―Ä―³–Η–Ζ–Φ
, –Κ–Ψ―²–Ψ―Ä―΄–Ι –Η–Ϋ–¥―É―Ü–Η―Ä―É–Β―² –Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Η–Ι –Η–Ζ–Ψ–Φ–Ψ―Ä―³–Η–Ζ–Φ 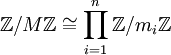 .
.
–£―΄–Ω–Ψ–Μ–Ϋ–Β–Ϋ–Η–Β –Α―Ä–Η―³–Φ–Β―²–Η―΅–Β―¹–Κ–Η―Ö –Ψ–Ω–Β―Ä–Α―Ü–Η–Ι
–Γ –Η―¹–Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α–Ϋ–Η–Β–Φ ―¹–Η―¹―²–Β–Φ―΄ –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Φ–Ψ–Ε–Ϋ–Ψ –≤―΄–Ω–Ψ–Μ–Ϋ―è―²―¨ –Ψ―¹–Ϋ–Ψ–≤–Ϋ―΄–Β –Α―Ä–Η―³–Φ–Β―²–Η―΅–Β―¹–Κ–Η–Β –Ψ–Ω–Β―Ä–Α―Ü–Η–Η.
–Γ–Μ–Ψ–Ε–Β–Ϋ–Η–Β –Η –≤―΄―΅–Η―²–Α–Ϋ–Η–Β
–ü―É―¹―²―¨ 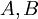 - –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ―΄–Β –Ϋ–Α―²―É―Ä–Α–Μ―¨–Ϋ―΄–Β ―΅–Η―¹–Μ–Α. –ü–Ψ–Μ–Ψ–Ε–Η–Φ, ―΅―²–Ψ
- –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ―΄–Β –Ϋ–Α―²―É―Ä–Α–Μ―¨–Ϋ―΄–Β ―΅–Η―¹–Μ–Α. –ü–Ψ–Μ–Ψ–Ε–Η–Φ, ―΅―²–Ψ 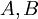 –Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è―é―²―¹―è –≤ –≤–Η–¥–Β ―¹–Η―¹―²–Β–Φ―΄ –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Κ–Α–Κ
–Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è―é―²―¹―è –≤ –≤–Η–¥–Β ―¹–Η―¹―²–Β–Φ―΄ –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Κ–Α–Κ 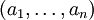 –Η
–Η 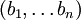 ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –Λ–Ψ―Ä–Φ–Α–Μ―¨–Ϋ–Ψ,
―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –Λ–Ψ―Ä–Φ–Α–Μ―¨–Ϋ–Ψ, 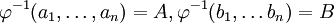 . –£ ―¹–Η–Μ―É ―²–Ψ–≥–Ψ, ―΅―²–Ψ
. –£ ―¹–Η–Μ―É ―²–Ψ–≥–Ψ, ―΅―²–Ψ 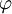 - –Η–Ζ–Ψ–Φ–Ψ―Ä―³–Η–Ζ–Φ –±―É–¥–Β–Φ –Η–Φ–Β―²―¨
- –Η–Ζ–Ψ–Φ–Ψ―Ä―³–Η–Ζ–Φ –±―É–¥–Β–Φ –Η–Φ–Β―²―¨ 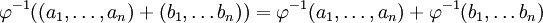 . –û–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ ―΅–Β―Ä–Β–Ζ
. –û–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ ―΅–Β―Ä–Β–Ζ 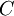 –Ψ―¹―²–Α―²–Ψ–Κ
–Ψ―¹―²–Α―²–Ψ–Κ 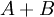 –Ψ―² –¥–Β–Μ–Β–Ϋ–Η―è –Ϋ–Α
–Ψ―² –¥–Β–Μ–Β–Ϋ–Η―è –Ϋ–Α 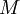 . –Δ–Ψ–≥–¥–Α
. –Δ–Ψ–≥–¥–Α 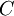 –Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è–Β―²―¹―è –≤ –≤–Η–¥–Β ―¹–Η―¹―²–Β–Φ―΄ –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Κ–Α–Κ
–Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è–Β―²―¹―è –≤ –≤–Η–¥–Β ―¹–Η―¹―²–Β–Φ―΄ –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Κ–Α–Κ 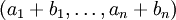 .
.
–Θ–Φ–Ϋ–Ψ–Ε–Β–Ϋ–Η–Β
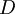 - –Ψ―¹―²–Α―²–Ψ–Κ –Ψ―² –¥–Β–Μ–Β–Ϋ–Η―è
- –Ψ―¹―²–Α―²–Ψ–Κ –Ψ―² –¥–Β–Μ–Β–Ϋ–Η―è 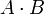 –Ϋ–Α
–Ϋ–Α 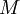 . –Δ–Ψ–≥–¥–Α
. –Δ–Ψ–≥–¥–Α 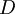 –Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è–Β―²―¹―è –≤ –≤–Η–¥–Β ―¹–Η―¹―²–Β–Φ―΄ –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Κ–Α–Κ
–Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è–Β―²―¹―è –≤ –≤–Η–¥–Β ―¹–Η―¹―²–Β–Φ―΄ –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Κ–Α–Κ 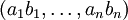 .
.
–î–Β–Μ–Β–Ϋ–Η–Β
–î–Β–Μ–Β–Ϋ–Η–Β  –Ϋ–Α
–Ϋ–Α 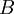 ―¹ –Η―¹–Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α–Ϋ–Η–Β–Φ ―¹–Η―¹―²–Β–Φ―΄ –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Φ–Ψ–Ε–Ϋ–Ψ –≤―΄–Ω–Ψ–Μ–Ϋ―è―²―¨ –Ϋ–Β –≤―¹–Β–≥–¥–Α. –ü–Ψ–Μ–Ψ–Ε–Η–Φ, ―΅―²–Ψ
―¹ –Η―¹–Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α–Ϋ–Η–Β–Φ ―¹–Η―¹―²–Β–Φ―΄ –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ –Φ–Ψ–Ε–Ϋ–Ψ –≤―΄–Ω–Ψ–Μ–Ϋ―è―²―¨ –Ϋ–Β –≤―¹–Β–≥–¥–Α. –ü–Ψ–Μ–Ψ–Ε–Η–Φ, ―΅―²–Ψ 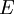 - –Ψ―¹―²–Α―²–Ψ–Κ
- –Ψ―¹―²–Α―²–Ψ–Κ 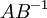 –Ψ―² –¥–Β–Μ–Β–Ϋ–Η―è –Ϋ–Α
–Ψ―² –¥–Β–Μ–Β–Ϋ–Η―è –Ϋ–Α 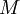 . –ù–Α ―è–Ζ―΄–Κ–Β ―²–Β–Ψ―Ä–Η–Η –Κ–Ψ–Μ–Β―Ü ―ç―²–Ψ –Ψ–Ζ–Ϋ–Α―΅–Α–Β―², ―΅―²–Ψ
. –ù–Α ―è–Ζ―΄–Κ–Β ―²–Β–Ψ―Ä–Η–Η –Κ–Ψ–Μ–Β―Ü ―ç―²–Ψ –Ψ–Ζ–Ϋ–Α―΅–Α–Β―², ―΅―²–Ψ 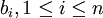 –Ψ–±―Ä–Α―²–Η–Φ –Η
–Ψ–±―Ä–Α―²–Η–Φ –Η 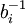 - –Ψ–±―Ä–Α―²–Ϋ―΄–Ι. –Δ–Ψ–≥–¥–Α
- –Ψ–±―Ä–Α―²–Ϋ―΄–Ι. –Δ–Ψ–≥–¥–Α 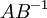 –Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è–Β―²―¹―è –≤ –≤–Η–¥–Β
–Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è–Β―²―¹―è –≤ –≤–Η–¥–Β 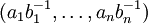 .
.
–Λ–Α–Κ―²–Ψ―Ä–Η–Ζ–Α―Ü–Η―è –Ω–Ψ–Μ―É–Ω―Ä–Ψ―¹―²―΄―Ö ―΅–Η―¹–Β–Μ
–ü―É―¹―²―¨ 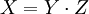 - –Ω–Ψ–Μ―É–Ω―Ä–Ψ―¹―²–Ψ–Β ―΅–Η―¹–Μ–Ψ. –†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―¹–Η―¹―²–Β–Φ―É –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤
- –Ω–Ψ–Μ―É–Ω―Ä–Ψ―¹―²–Ψ–Β ―΅–Η―¹–Μ–Ψ. –†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―¹–Η―¹―²–Β–Φ―É –Ψ―¹―²–Α―²–Ψ―΅–Ϋ―΄―Ö –Κ–Μ–Α―¹―¹–Ψ–≤ 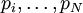 , –≥–¥–Β
, –≥–¥–Β 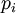 βÄî
βÄî 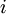 -–Β –Ω―Ä–Ψ―¹―²–Ψ–Β ―΅–Η―¹–Μ–Ψ.
-–Β –Ω―Ä–Ψ―¹―²–Ψ–Β ―΅–Η―¹–Μ–Ψ.