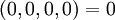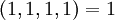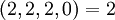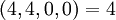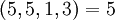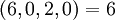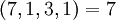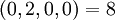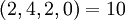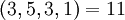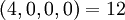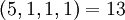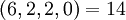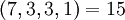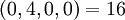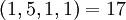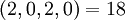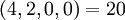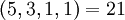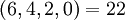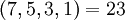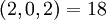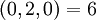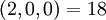Схема коррекции ошибок Rajendra S. Katti
Myachikov (обсуждение | вклад) |
Turbo (обсуждение | вклад) |
||
| (не показаны 2 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
== Введение == | == Введение == | ||
| − | + | Традиционный метод коррекции ошибок, основан на использовании избыточной системы остаточных классов с взаимнопростыми основаниями. Недостатки представления чисел в такой системе с целью коррекции ошибок при вычислениях покажем на примере. | |
Пусть избыточная СОК определяется следующими модулями <math> m_1 = 3, m_2 = 4, m_3 = 5, m_4 = 7</math>, а динамический диапазон определяется <math>m_1</math> и <math>m_2</math> и соответственно равен <math>\{0,...,11\}</math>, а модули <math>m_3, m_4</math> являются дополнительными и необходимы для проверки на ошибки. | Пусть избыточная СОК определяется следующими модулями <math> m_1 = 3, m_2 = 4, m_3 = 5, m_4 = 7</math>, а динамический диапазон определяется <math>m_1</math> и <math>m_2</math> и соответственно равен <math>\{0,...,11\}</math>, а модули <math>m_3, m_4</math> являются дополнительными и необходимы для проверки на ошибки. | ||
| Строка 12: | Строка 12: | ||
== Модули, имеющие общие делители == | == Модули, имеющие общие делители == | ||
| − | Каждый набор остатков необязательно соответствует числу из динамического диапазона, если модули не являются попарно взаимно простыми. Легко показать, что такое соответствие есть тогда и только тогда, когда | + | Каждый набор остатков необязательно соответствует числу из динамического диапазона, если модули не являются попарно взаимно простыми. Легко показать, что такое соответствие есть тогда и только тогда, когда равенство |
:<math>|r_i|_k = |r_j|_k</math>, | :<math>|r_i|_k = |r_j|_k</math>, | ||
выполняется для любых <math>i, j</math>, где <math>k = gcd(r_i, r_j)</math>. Таким образом, ошибочный разряд может быть найден выполнением только простой операции вычисления остатка. | выполняется для любых <math>i, j</math>, где <math>k = gcd(r_i, r_j)</math>. Таким образом, ошибочный разряд может быть найден выполнением только простой операции вычисления остатка. | ||
| Строка 124: | Строка 124: | ||
Начнём описание алгоритма со следующей леммы. | Начнём описание алгоритма со следующей леммы. | ||
| − | '''Лемма 1'''. Существует и единственно кодовое слово в множестве <math>A</math> | + | '''Лемма 1'''. Существует и единственно кодовое слово в множестве <math>A</math>, такое что кодовое расстояние между этим словом и остаточным представлением <math>(r_1, r_2, r_3, r_4)</math> равно <math>1</math>. |
| + | |||
| + | Опишем теперь коррекцию ошибки для каждого варианта: | ||
| + | #Кодовое слово за пределами динамического диапазона и совместно. | ||
| + | #Кодовое слово не совместно. | ||
| + | |||
| + | '''Вариант 1'''. Пусть остаточное представление <math>(r_1, r_2, r_3, r_4)</math> соответствует целому <math>R</math>. Так как только один разряд ошибочный, то <math>R</math> принадлежит множеству <math>C</math>. Коррекция выполняется следующим образом: | ||
| + | #Для всех кортежей из трёх остатков вычислить по КТО соответствующее целое. | ||
| + | #Если полученное целое принадлежит динамическому диапазону, то ошибка в исключённом разряде. | ||
| + | #Предположим без потери общности, что ошибочным является <math>r_3</math>. Найдём правильное значение <math>\bar {r_3}</math> из следующих уравнений: | ||
| + | :<math>|\bar{r_3}|_{k_a} = |r_1|_{k_a}, k_a = gcd(m_3, m_1)</math>, | ||
| + | :<math>|\bar{r_3}|_{k_b} = |r_2|_{k_b}, k_b = gcd(m_3, m_2)</math>, | ||
| + | :<math>|\bar{r_3}|_{k_c} = |r_4|_{k_c}, k_c = gcd(m_3, m_4)</math>. | ||
| + | |||
| + | Если полученных решений несколько, то согласно Лемме 1 только одно из них принадлежит динамическому диапазону. | ||
| + | |||
| + | '''Вариант 2'''. Пусть кодовое слово <math>(r_1, r_2, r_3, r_4)</math> не является совместным, то есть не выполняется равенство: | ||
| + | :<math>|r_i|_{k_a} = |r_j|_{k_a}, k_a = gcd(m_i, m_j)</math>. | ||
| + | |||
| + | Значит ошибочным является либо <math>r_i</math>, либо <math>r_j</math>. Пусть ошибка в <math>r_i</math>, найдём правильное значение, как в шаге 3 выше. Если для полученных решений, соответствующие целые не лежат в динамическом диапазоне, то ошибка в <math>r_j</math>, и её можно исправить тем же способом, описанным в шаге 3. | ||
| + | |||
| + | ==== Примеры ==== | ||
| + | Определим множество модулей <math>(m_1, m_2, m_3, m_4) = (8,6,4,2)</math>. Все кодовые слова и их целые эквиваленты приведены ниже: | ||
| + | :<math>(0,0,0,0) = 0</math> | ||
| + | :<math>(1,1,1,1) = 1</math> | ||
| + | :<math>(2,2,2,0) = 2</math> | ||
| + | :<math>(3,3,3,1) = 3</math> | ||
| + | :<math>(4,4,0,0) = 4</math> | ||
| + | :<math>(5,5,1,3) = 5</math> | ||
| + | :<math>(6,0,2,0) = 6</math> | ||
| + | :<math>(7,1,3,1) = 7</math> | ||
| + | :<math>(0,2,0,0) = 8</math> | ||
| + | :<math>(1,3,1,1) = 9</math> | ||
| + | :<math>(2,4,2,0) = 10</math> | ||
| + | :<math>(3,5,3,1) = 11</math> | ||
| + | :<math>(4,0,0,0) = 12</math> | ||
| + | :<math>(5,1,1,1) = 13</math> | ||
| + | :<math>(6,2,2,0) = 14</math> | ||
| + | :<math>(7,3,3,1) = 15</math> | ||
| + | :<math>(0,4,0,0) = 16</math> | ||
| + | :<math>(1,5,1,1) = 17</math> | ||
| + | :<math>(2,0,2,0) = 18</math> | ||
| + | :<math>(3,1,3,1) = 19</math> | ||
| + | :<math>(4,2,0,0) = 20</math> | ||
| + | :<math>(5,3,1,1) = 21</math> | ||
| + | :<math>(6,4,2,0) = 22</math> | ||
| + | :<math>(7,5,3,1) = 23</math> | ||
| + | |||
| + | Множества <math>A, B, C</math>, определённые выше, равны <math>A = \{0, ..., 3\}, B = \{4, ..., 7\}, C = \{8, ..., 23\}</math>. | ||
| + | |||
| + | Рассмотрим теперь несколько примеров обнаружения и коррекции. | ||
| + | |||
| + | '''Пример 1 '''. Остаточное представление <math>(r_1, r_2, r_3, r_4) = (2,0,2,0)</math> является совместным и не принадлежит динамическому диапазону. Четыре кортежа из трёх остатков и соответствующие им целые: | ||
| + | :<math>(2,0,2) = 18</math> | ||
| + | :<math>(0,2,0) = 6</math> | ||
| + | :<math>(2,0,0) = 18</math> | ||
| + | :<math>(2,2,0) = 2</math> | ||
| + | |||
| + | Единственное представление, лежащее в <math>\{0, ..., 3\}</math> - это <math>(2,2,0)</math>, следовательно <math>r_2 = 0</math> является ошибочным. Эта ошибка может быть исправлена, правильное значение можно найти из следующих уравнений: | ||
| + | :<math>|\bar {r_2}|_2 = |r_1|_2 = 0</math>, | ||
| + | :<math>|\bar {r_2}|_2 = |r_3|_2 = 0</math>, | ||
| + | :<math>|\bar {r_2}|_2 = |r_4|_2 = 0</math>, | ||
| + | :<math>\bar {r_2} \leq 5</math>. | ||
| + | |||
| + | Им удовлетворяют три решения: <math>0, 2, 4</math>. Правильным является <math> \bar {r_2} = 2</math>, так оставшиеся два соответствуют представлениям, лежащим вне динамического диапазона. | ||
| + | |||
| + | '''Пример 2 '''. Остаточное представление <math>(r_1, r_2, r_3, r_4) = (0,0,0,5)</math>. Так как <math>r_4 \geq 2</math>, то <math>r_4</math> - ошибочный. Найдём правильное значение из следующих уравнений: | ||
| + | :<math>|\bar {r_4}|_2 = |r_1|_2 = 0</math>, | ||
| + | :<math>|\bar {r_4}|_2 = |r_2|_2 = 0</math>, | ||
| + | :<math>|\bar {r_4}|_2 = |r_3|_2 = 0</math>, | ||
| + | :<math>\bar {r_4} \leq 1</math>. | ||
| + | |||
| + | Получаем <math>\bar {r_4} = 1</math>. | ||
| + | |||
| + | '''Пример 3 '''. Остаточное представление <math>(r_1, r_2, r_3, r_4) = (1,3,3,1)</math> является несовместным, так как не выполняется следующее равенство: | ||
| + | :<math>|r_1|_4 = |r_3|_4</math>. | ||
| + | |||
| + | Пусть <math>r_3</math> - ошибочный. Тогда скорректированное значение <math>r_3</math> может быть найдено из следующих уравнений: | ||
| + | :<math>|\bar {r_3}|_4 = |r_1|_4 = 1</math>, | ||
| + | :<math>|\bar {r_3}|_2 = |r_2|_2 = 1</math>, | ||
| + | :<math>|\bar {r_3}|_2 = |r_4|_2 = 1</math>, | ||
| + | :<math>\bar {r_3} \leq 3</math>. | ||
| + | |||
| + | Решая, находим <math> \bar {r_3} = 1 </math>. Скорректированное остаточное представление <math>(1,3,1,1) = 9</math> лежит вне динамического диапазона. Значит, ошибочным является <math>r_1</math>. Проводя аналогичную процедуру, находим <math>r_1 = 3</math>. Полученное остаточное представление <math>(3,3,3,1) = 3</math> лежит в динамическом диапазоне, коррекция завершена. Заметим, что мы пытались обнаружить ошибку в остаточном представлении <math>(1,3,3,1)</math>, которое имеет кодовое расстояние равное <math>1</math> с совместными представлениями <math>(1,3,1,1)</math> и <math>(3,3,3,1)</math>. По Лемме 1 только одно из них лежит в динамическом диапазоне. | ||
| + | == Литература == | ||
| + | Rajendra S. Katti, A New Residue Arithmetic Error Correction Scheme, IEEE Trans. Computers, 1996, том 45, стр. 13-19 | ||
Текущая версия на 11:35, 26 мая 2014
Содержание |
[править] Введение
Традиционный метод коррекции ошибок, основан на использовании избыточной системы остаточных классов с взаимнопростыми основаниями. Недостатки представления чисел в такой системе с целью коррекции ошибок при вычислениях покажем на примере.
Пусть избыточная СОК определяется следующими модулями 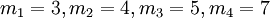 , а динамический диапазон определяется
, а динамический диапазон определяется 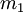 и
и 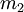 и соответственно равен
и соответственно равен 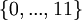 , а модули
, а модули 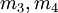 являются дополнительными и необходимы для проверки на ошибки.
являются дополнительными и необходимы для проверки на ошибки.
Натуральное число из динамического диапазона может быть восстановлено по любым трём из четырёх остатков по представленным модулям. Например, число 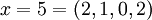 может быть представлено как
может быть представлено как 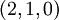 в системе модулей
в системе модулей 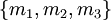 или
или 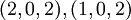 в системах
в системах 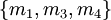 и
и 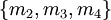 соответственно. Поэтому, если одна цифра отбрасывается в представлении
соответственно. Поэтому, если одна цифра отбрасывается в представлении 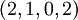 , правильный результат восстановления будет получен тогда и только тогда, когда отбрасываемая цифра ошибочна. Итак, обнаружение ошибок и коррекция выполняется следующим образом:
, правильный результат восстановления будет получен тогда и только тогда, когда отбрасываемая цифра ошибочна. Итак, обнаружение ошибок и коррекция выполняется следующим образом:
- Если число лежит вне динамического диапазона - произошла ошибка.
- Остатки отбрасываются по одному и если в результате одного из отбрасываний полученное число лежит в динамическом диапазоне, то отброшенный остаток является ошибочным.
- Корректное значение остатка получается расширением полученного на шаге 2 множества модулей, остатки по которым не содержат ошибок.
Такой подход требует много времени и вычислительных ресурсов. Ниже будет предложена новая схема обнаружения и коррекции ошибок на основе СОК.
[править] Модули, имеющие общие делители
Каждый набор остатков необязательно соответствует числу из динамического диапазона, если модули не являются попарно взаимно простыми. Легко показать, что такое соответствие есть тогда и только тогда, когда равенство
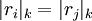 ,
,
выполняется для любых 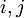 , где
, где 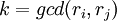 . Таким образом, ошибочный разряд может быть найден выполнением только простой операции вычисления остатка.
. Таким образом, ошибочный разряд может быть найден выполнением только простой операции вычисления остатка.
Приведём пример, демонстрирующий, как можно проверить набор остатков на наличие ошибок. Проверим набор 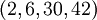 в системе модулей
в системе модулей 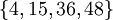 . Наибольшие общие делители всевозможных пар модулей соответственно равны:
. Наибольшие общие делители всевозможных пар модулей соответственно равны: 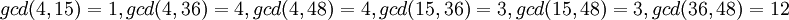 .
Используя описанное выше соотношение для проверки, получаем:
.
Используя описанное выше соотношение для проверки, получаем: 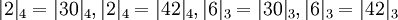 и
и 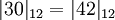 . То есть ошибок нет и число может быть восстановлено с использованием китайской теоремы об остатках (КТО) для модулей, имеющих нетривиальные общие делители.
. То есть ошибок нет и число может быть восстановлено с использованием китайской теоремы об остатках (КТО) для модулей, имеющих нетривиальные общие делители.
КТО для системы модулей, попарно не взаимно простых. Пусть есть представление 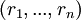 натурального числа
натурального числа  , определяемое системой модулей
, определяемое системой модулей 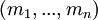 . Тогда
. Тогда
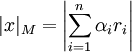 ,
,
где 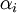 - число, такое что
- число, такое что 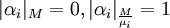 ,
где
,
где 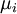 - числа, такие что
- числа, такие что 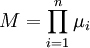 ,
, 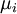 делит
делит 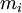 и
и 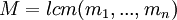 . Если для некоторого
. Если для некоторого 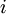 такое
такое 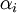 не существует, то соответствующее слагаемое в сумме опускается.
не существует, то соответствующее слагаемое в сумме опускается.
Операции над числами остаются корректными и в системе не взаимно простых попарно модулей.
[править] Алгоритм
Если в множестве модулей 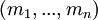 есть имеющие нетривиальный общий делитель, то каждый набор остатков
есть имеющие нетривиальный общий делитель, то каждый набор остатков 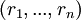 необязательно соответствует некоторому числу. Каждый набор, для которого такое соответствие имеет место, будем называть кодовым словом.
необязательно соответствует некоторому числу. Каждый набор, для которого такое соответствие имеет место, будем называть кодовым словом.
Расстоянием между двумя представлениями чисел в СОК(кодовыми словами) будем считать количество разрядов, в которых кодовые слова различаются между собой.
Кодовым расстоянием назовём минимальное расстояние среди всех пар кодовых слов.
Чтобы обнаружить и исправить 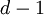 или меньше ошибок, необходимо и достаточно, чтобы кодовое расстояние было не меньше
или меньше ошибок, необходимо и достаточно, чтобы кодовое расстояние было не меньше 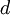 . Не более
. Не более 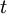 ошибок может быть обнаружено и исправлено тогда и только тогда, когда кодовое расстояние больше, чем
ошибок может быть обнаружено и исправлено тогда и только тогда, когда кодовое расстояние больше, чем 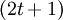 . Если кодовое расстояние больше или равно, чем
. Если кодовое расстояние больше или равно, чем 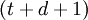 , то любая комбинация из
, то любая комбинация из 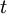 ошибок может быть исправлена и до
ошибок может быть исправлена и до 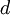 ошибок могут быть обнаружены.
Для множества из
ошибок могут быть обнаружены.
Для множества из  модулей в соответствующей системе могут быть представлены числа
модулей в соответствующей системе могут быть представлены числа 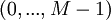 , где
, где 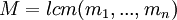 .
.
Циклическим числом 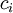 для каждого модуля
для каждого модуля 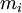 назовём
назовём 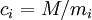 .
.
[править] Модули с попарно взаимно простыми циклическими числами
Построим теперь систему модулей с попарно взаимно простыми циклическими числами, которая поможет получит эффективный алгоритм обнаружения и коррекции ошибок.
Построение 1.
- Выберем
 попарно взаимно простых циклических чисел, не равных единице
попарно взаимно простых циклических чисел, не равных единице 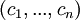 .
.
- Получим систему модулей
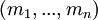 следующим образом:
следующим образом:
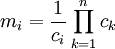 .
.
Полученные модули обладают двумя свойствами:
- Наименьшие общие кратны всевозможных пар модулей равны между собой.
- Наибольшие общие делители всевозможных пар модулей различны.
Теорема 1. Для построенной системы модулей кодовое расстояние равно 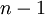 , где
, где  - количество модулей.
- количество модулей.
[править] Алгоритм обнаружения ошибки
- Если
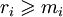 , то произошла ошибка в
, то произошла ошибка в 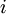 -том разряде.
-том разряде.
- Если не выполняется хотя бы одно из следующей системы равенств:
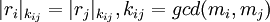 ,
,
то произошла ошибка.
Теорема 2. Для системы из четырёх модулей 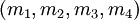 ошибка в одном разряде влечёт за собой невыполнением как минимум двух, а как максимум трёх равенств из системы выше. Причём, если ошибка в
ошибка в одном разряде влечёт за собой невыполнением как минимум двух, а как максимум трёх равенств из системы выше. Причём, если ошибка в 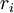 , то равенства, которые не выполняются, содержат
, то равенства, которые не выполняются, содержат 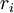 .
.
[править] Алгоритм локализации ошибки
Теорема 2 даёт алгоритм локализации ошибки. Ошибочным является разряд, который содержится во всех равенствах, которые не выполняются.
[править] Алгоритм коррекции ошибки
Предложим, что ошибка в 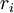 и
и 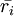 - правильное значение. Тогда
- правильное значение. Тогда 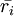 можно найти, решая следующую систему уравнений:
можно найти, решая следующую систему уравнений:
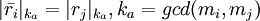 ,
,
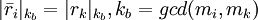 .
.
Решение заключается в составлении множеств  и
и 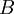 :
:
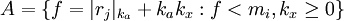 ,
,
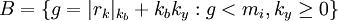 .
.
и поиске пересечения 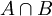 . Можно доказать, что такое пересечение всегда непусто и состоит ровно из одного элемента.
. Можно доказать, что такое пересечение всегда непусто и состоит ровно из одного элемента.
[править] Примеры
Пример обнаружения одной ошибки.
Воспользуемся Построением 1 для получения системы модулей. Используя попарно взаимно простые циклические числа 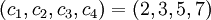 , получим систему модулей
, получим систему модулей 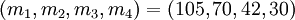 . Пусть теперь в остаточном представлении
. Пусть теперь в остаточном представлении 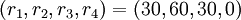 содержится одна ошибка. Проверяя совместность представления, найдём, что следующие равенства не выполняются:
содержится одна ошибка. Проверяя совместность представления, найдём, что следующие равенства не выполняются:
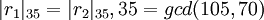 ,
,
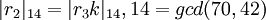 .
.
Так как 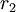 является общим в этих равенствах, ошибочным является остаток
является общим в этих равенствах, ошибочным является остаток 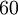 . Для того чтобы получить правильное значение, составим множества
. Для того чтобы получить правильное значение, составим множества  и
и 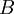 как было описано выше:
как было описано выше:
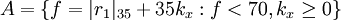 ,
,
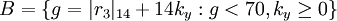 .
.
Получим:
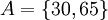 ,
,
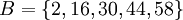 .
.
Таким образом скорректированное значение 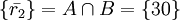 .
.
Необязательно вычислять множество 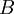 полностью. Так как
полностью. Так как 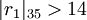 , то
, то 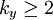 . Вычисления элементов множеств следует прекратить, как только их пересечение больше не пусто.
Пример обнаружения двух и коррекции одной ошибки.
Для обнаружения двух и коррекции одной ошибки требуется по крайней мере 5 модулей и кодовое расстояние равное 4. Если мы выберем циклические числа
. Вычисления элементов множеств следует прекратить, как только их пересечение больше не пусто.
Пример обнаружения двух и коррекции одной ошибки.
Для обнаружения двух и коррекции одной ошибки требуется по крайней мере 5 модулей и кодовое расстояние равное 4. Если мы выберем циклические числа 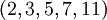 мы получим набор модулей
мы получим набор модулей 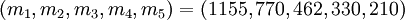 . Чтобы проверить, есть ли ошибки в остаточном представлении
. Чтобы проверить, есть ли ошибки в остаточном представлении 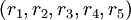 , нужно выяснить, какие из следующих равенств не выполняются:
, нужно выяснить, какие из следующих равенств не выполняются:
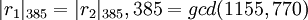 ,
,
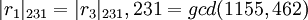 ,
,
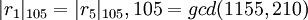 ,
,
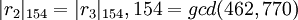 ,
,
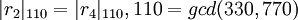 ,
,
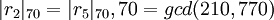 ,
,
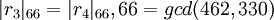 ,
,
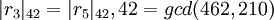 ,
,
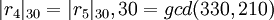 .
.
Следует отметить, что если три или четыре из равенств выше не выполняются, то обнаружена одна ошибка. Если их пять и больше, то ошибок две. Аналогично предыдущему примеру, можно построить три множества 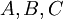 . Исправленное значение ошибочного разряда получим, найдя пересечение этих множеств:
. Исправленное значение ошибочного разряда получим, найдя пересечение этих множеств:
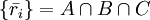 .
.
[править] Модули с произвольными циклическими числами
Если мы уберём ограничение на взаимную простоту циклических числе, то обнаружение и коррекция ошибки может быть всё ещё осуществлена сокращением динамического диапазона. Следующие теорема и следствие связывают кодовое расстояние и динамический диапазон.
Теорема 3. Пусть есть множество модулей 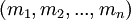 и
и 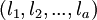 - множество наименьших общих кратных всевозможных различных пар модулей, где
- множество наименьших общих кратных всевозможных различных пар модулей, где 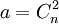 . Тогда, если
. Тогда, если 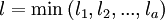 , то кодовое расстояние множества всех представлений чисел
, то кодовое расстояние множества всех представлений чисел 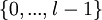 в системе остаточных классов равно
в системе остаточных классов равно 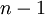 .
.
Следствие. Пусть есть множество модулей 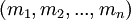 и
и 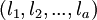 - множество наименьших общих кратных всевозможных кортежей из
- множество наименьших общих кратных всевозможных кортежей из 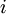 различных модулей, где
различных модулей, где 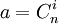 . Тогда, если
. Тогда, если 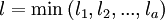 , то кодовое расстояние множества всех представлений чисел
, то кодовое расстояние множества всех представлений чисел 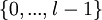 в системе остаточных классов равно
в системе остаточных классов равно 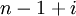 .
.
Далее будем предполагать, что ошибочный разряд только один. Из теоремы 3 следует, что для коррекции одной ошибки требуется множество из 4 модулей 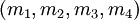 . Пусть
. Пусть 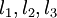 - соответственно наименьшее из НОК всех пар, наименьшее из НОК всех троек и НОК всех модулей. Из теоремы 3 и следствия из неё следует, что для множества чисел
- соответственно наименьшее из НОК всех пар, наименьшее из НОК всех троек и НОК всех модулей. Из теоремы 3 и следствия из неё следует, что для множества чисел 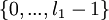 кодовое расстояние соответствующего множества кодовых слов равно
кодовое расстояние соответствующего множества кодовых слов равно 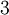 , а для множеств
, а для множеств 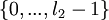 и
и 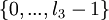 - не меньше
- не меньше 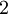 и не меньше
и не меньше  соответственно. Разделим множество всех кодовых слов на три подмножества:
соответственно. Разделим множество всех кодовых слов на три подмножества:
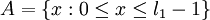 ,
,
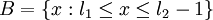 ,
,
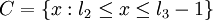 .
.
Для коррекции одной ошибки необходимо кодовое расстояние, равное трём, то есть все слова из  и
и 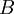 выходят за границы динамического диапазона. Пусть необходимо обнаружить/исправить одну ошибку в остаточном представлении.
выходят за границы динамического диапазона. Пусть необходимо обнаружить/исправить одну ошибку в остаточном представлении.
[править] Алгоритм обнаружения ошибки
- Если
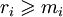 , то произошла ошибка в
, то произошла ошибка в 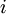 -том разряде.
-том разряде.
- Если остаточное представление не является совместным и слово не лежит в динамическом диапазоне, то произошла ошибка. Для проверки нужно воспользоваться КТО для перевода числа из остаточного представления и проверить, выполняется ли
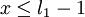 .
.
- Если остаточное представление не является совместным, то произошла ошибка.
- Если остаточное представление является совместным и лежит в динамическом диапазоне, то ошибок нет.
[править] Алгоритм коррекции ошибки
Начнём описание алгоритма со следующей леммы.
Лемма 1. Существует и единственно кодовое слово в множестве  , такое что кодовое расстояние между этим словом и остаточным представлением
, такое что кодовое расстояние между этим словом и остаточным представлением 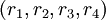 равно
равно 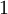 .
.
Опишем теперь коррекцию ошибки для каждого варианта:
- Кодовое слово за пределами динамического диапазона и совместно.
- Кодовое слово не совместно.
Вариант 1. Пусть остаточное представление 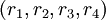 соответствует целому
соответствует целому 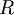 . Так как только один разряд ошибочный, то
. Так как только один разряд ошибочный, то 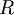 принадлежит множеству
принадлежит множеству 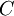 . Коррекция выполняется следующим образом:
. Коррекция выполняется следующим образом:
- Для всех кортежей из трёх остатков вычислить по КТО соответствующее целое.
- Если полученное целое принадлежит динамическому диапазону, то ошибка в исключённом разряде.
- Предположим без потери общности, что ошибочным является
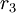 . Найдём правильное значение
. Найдём правильное значение 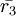 из следующих уравнений:
из следующих уравнений:
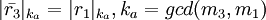 ,
,
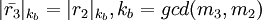 ,
,
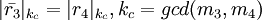 .
.
Если полученных решений несколько, то согласно Лемме 1 только одно из них принадлежит динамическому диапазону.
Вариант 2. Пусть кодовое слово 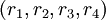 не является совместным, то есть не выполняется равенство:
не является совместным, то есть не выполняется равенство:
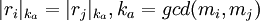 .
.
Значит ошибочным является либо 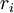 , либо
, либо 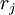 . Пусть ошибка в
. Пусть ошибка в 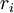 , найдём правильное значение, как в шаге 3 выше. Если для полученных решений, соответствующие целые не лежат в динамическом диапазоне, то ошибка в
, найдём правильное значение, как в шаге 3 выше. Если для полученных решений, соответствующие целые не лежат в динамическом диапазоне, то ошибка в 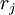 , и её можно исправить тем же способом, описанным в шаге 3.
, и её можно исправить тем же способом, описанным в шаге 3.
[править] Примеры
Определим множество модулей 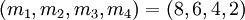 . Все кодовые слова и их целые эквиваленты приведены ниже:
. Все кодовые слова и их целые эквиваленты приведены ниже:
Множества 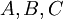 , определённые выше, равны
, определённые выше, равны 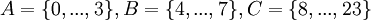 .
.
Рассмотрим теперь несколько примеров обнаружения и коррекции.
Пример 1 . Остаточное представление 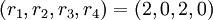 является совместным и не принадлежит динамическому диапазону. Четыре кортежа из трёх остатков и соответствующие им целые:
является совместным и не принадлежит динамическому диапазону. Четыре кортежа из трёх остатков и соответствующие им целые:
Единственное представление, лежащее в 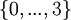 - это
- это 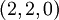 , следовательно
, следовательно 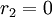 является ошибочным. Эта ошибка может быть исправлена, правильное значение можно найти из следующих уравнений:
является ошибочным. Эта ошибка может быть исправлена, правильное значение можно найти из следующих уравнений:
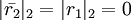 ,
,
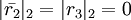 ,
,
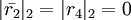 ,
,
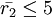 .
.
Им удовлетворяют три решения: 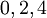 . Правильным является
. Правильным является 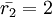 , так оставшиеся два соответствуют представлениям, лежащим вне динамического диапазона.
, так оставшиеся два соответствуют представлениям, лежащим вне динамического диапазона.
Пример 2 . Остаточное представление 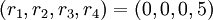 . Так как
. Так как 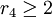 , то
, то 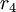 - ошибочный. Найдём правильное значение из следующих уравнений:
- ошибочный. Найдём правильное значение из следующих уравнений:
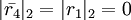 ,
,
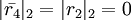 ,
,
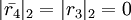 ,
,
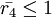 .
.
Получаем 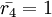 .
.
Пример 3 . Остаточное представление 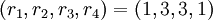 является несовместным, так как не выполняется следующее равенство:
является несовместным, так как не выполняется следующее равенство:
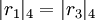 .
.
Пусть 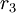 - ошибочный. Тогда скорректированное значение
- ошибочный. Тогда скорректированное значение 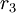 может быть найдено из следующих уравнений:
может быть найдено из следующих уравнений:
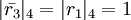 ,
,
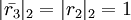 ,
,
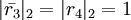 ,
,
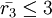 .
.
Решая, находим 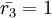 . Скорректированное остаточное представление
. Скорректированное остаточное представление 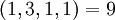 лежит вне динамического диапазона. Значит, ошибочным является
лежит вне динамического диапазона. Значит, ошибочным является 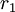 . Проводя аналогичную процедуру, находим
. Проводя аналогичную процедуру, находим 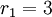 . Полученное остаточное представление
. Полученное остаточное представление 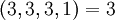 лежит в динамическом диапазоне, коррекция завершена. Заметим, что мы пытались обнаружить ошибку в остаточном представлении
лежит в динамическом диапазоне, коррекция завершена. Заметим, что мы пытались обнаружить ошибку в остаточном представлении 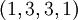 , которое имеет кодовое расстояние равное
, которое имеет кодовое расстояние равное 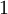 с совместными представлениями
с совместными представлениями 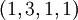 и
и 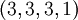 . По Лемме 1 только одно из них лежит в динамическом диапазоне.
. По Лемме 1 только одно из них лежит в динамическом диапазоне.
[править] Литература
Rajendra S. Katti, A New Residue Arithmetic Error Correction Scheme, IEEE Trans. Computers, 1996, том 45, стр. 13-19