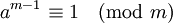Функция Эйлера

Материал из Модулярная арифметики
(Различия между версиями)
Перейти к: навигация, поиск
(Новая страница: «== Определение == '''Функция Эйлера''' <math>phi (n)</math> — это количество чисел от <math>1</math> до <math>n</m…»)
 
 
Строка 31: Строка 31:
 
</tr>
 
</tr>
 
</table>
 
</table>
 +
 +
Далее в ряде [http://oeis.org/A000010 A000010 в энциклопедии OEIS].
 +
 +
== Свойства ==
 +
* Если <math>p</math> — простое число, то <math>phi(p)=p-1</math>.
 +
'''Пояснение''': Это очевидно, т.к. любое число, кроме самого p, взаимно просто с ним.
 +
* Если <math>p</math> — простое, <math>a</math> — натуральное число, то <math>phi(p^a)=p^a-p^{a-1}</math>.
 +
'''Пояснение''': Поскольку с числом <math>p^a</math> не взаимно просты только числа вида <math>pk (k \in \mathcal{N})</math>, которых <math>p^a / p = p^{a-1}</math> штук.
 +
* Если <math>a</math> и <math>b</math> взаимно простые, то <math>phi(ab) = phi(a) phi(b)</math> ("мультипликативность" функции Эйлера).
 +
'''Пояснение''': Этот факт следует из китайской теоремы об остатках.
 +
 +
== Функция Эйлера для произвольного <math>n</math> ==
 +
Функцию Эйлера можно получить для любого <math>n</math> через его факторизацию (разложение <math>n</math> на простые сомножители), используя свойства описанные выше. Если
 +
 +
<math>n = p_1^{a_1} \cdot p_2^{a_2} \cdot \ldots \cdot p_k^{a_k}</math>
 +
 +
(где все <math>p_i</math> — простые), то
 +
 +
<math>phi(n) = phi(p_1^{a_1}) \cdot phi(p_2^{a_2}) \cdot \ldots \cdot phi(p_k^{a_k})
 +
= (p_1^{a_1} - p_1^{a_1-1}) \cdot (p_2^{a_2} - p_2^{a_2-1}) \cdot \ldots \cdot (p_k^{a_k} - p_k^{a_k-1})
 +
= n \cdot \left( 1-{1\over p_1} \right) \cdot \left( 1-{1\over p_2} \right) \cdot \ldots \cdot \left( 1-{1\over p_k} \right)</math>
 +
 +
== Приложения ==
 +
Самое известное и важное свойство функции Эйлера выражается в теореме Эйлера:
 +
* <math>a^{phi(m)} \equiv 1 \pmod m</math>, где <math>a</math> и <math>m</math> взаимно просты.
 +
 +
В частном случае, когда <math>m</math> простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
 +
 +
* <math>a^{m-1} \equiv 1 \pmod m </math>
 +
 +
== Ссылки ==
 +
* [http://e-maxx.ru/algo/euler_function Функция Эйлера на e-maxx.ru (для программистов)]
 +
* [http://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%AD%D0%B9%D0%BB%D0%B5%D1%80%D0%B0 Функция Эйлера в Википедии (для математиков)]
 +
 +
== Реализация ==
 +
* Поиск значения функции Эйлера он-лайн (скоро)

Текущая версия на 11:19, 9 декабря 2013

Содержание

[править] Определение

Функция Эйлера 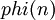phi (n) — это количество чисел от 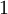1 до n, взаимно простых с n, т.е. это количество таких натуральных чисел из отрезка [1; n], наибольший общий делитель (НОД) которых с n равен единице.

Первые значения этой функции:

n 1 2 3 4 5 6 7 8 9 10
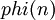phi(n) 1 1 2 2 4 2 6 4 6 4

Далее в ряде A000010 в энциклопедии OEIS.

[править] Свойства

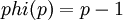  • Если p — простое число, то phi(p)=p-1.

Пояснение: Это очевидно, т.к. любое число, кроме самого p, взаимно просто с ним.

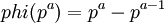  • Если p — простое, a — натуральное число, то phi(p^a)=p^a-p^{a-1}.

Пояснение: Поскольку с числом 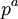p^a не взаимно просты только числа вида 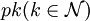pk (k \in \mathcal{N}), которых 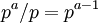p^a / p = p^{a-1} штук.

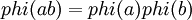  • Если a и b взаимно простые, то phi(ab) = phi(a) phi(b) ("мультипликативность" функции Эйлера).

Пояснение: Этот факт следует из китайской теоремы об остатках.

[править] Функция Эйлера для произвольного n

Функцию Эйлера можно получить для любого n через его факторизацию (разложение n на простые сомножители), используя свойства описанные выше. Если

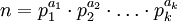
n = p_1^{a_1} \cdot p_2^{a_2} \cdot \ldots \cdot p_k^{a_k}

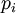(где все p_i — простые), то

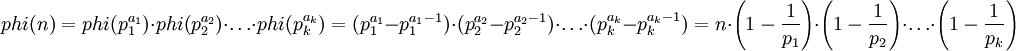
phi(n) = phi(p_1^{a_1}) \cdot phi(p_2^{a_2}) \cdot \ldots \cdot phi(p_k^{a_k}) = (p_1^{a_1} - p_1^{a_1-1}) \cdot (p_2^{a_2} - p_2^{a_2-1}) \cdot \ldots \cdot (p_k^{a_k} - p_k^{a_k-1}) = n \cdot \left( 1-{1\over p_1} \right) \cdot \left( 1-{1\over p_2} \right) \cdot \ldots \cdot \left( 1-{1\over p_k} \right)

[править] Приложения

Самое известное и важное свойство функции Эйлера выражается в теореме Эйлера:

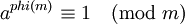  • a^{phi(m)} \equiv 1 \pmod m, где a и m взаимно просты.

В частном случае, когда m простое, теорема Эйлера превращается в так называемую малую теорему Ферма:

  • a^{m-1} \equiv 1 \pmod m

[править] Ссылки

[править] Реализация

  • Поиск значения функции Эйлера он-лайн (скоро)
Источник — «http://vscripts.ru/w/index.php?title=%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%AD%D0%B9%D0%BB%D0%B5%D1%80%D0%B0&oldid=788»
Персональные инструменты
Пространства имён

Варианты
Действия
Навигация