Теорема о делении с остатком. Алгоритм Евклида — различия между версиями
Материал из Модулярная арифметики
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 5: | Строка 5: | ||
Тогда имеем шесть классов разбиения множества целых чисел по модулю 6: | Тогда имеем шесть классов разбиения множества целых чисел по модулю 6: | ||
| − | :<math>K_0 = {\ldots,-18,-12,-6,0,6,12,18,\ldots}, r=0</math>; | + | :<math>K_0 = \left\{\ldots,-18,-12,-6,0,6,12,18,\ldots \right\}, r=0</math>; |
| − | :<math>K_1 = {\ldots,-17,-11,-5,1,7,13,19,\ldots}, r=1</math>; | + | :<math>K_1 = \left\{\ldots,-17,-11,-5,1,7,13,19,\ldots \right\}, r=1</math>; |
| − | :<math>K_2 = {\ldots,-16,-10,-4,2,8,14,20,\ldots}, r=2</math>; | + | :<math>K_2 = \left\{\ldots,-16,-10,-4,2,8,14,20,\ldots \right\}, r=2</math>; |
| − | :<math>K_3 = {\ldots,-15,-9,-3,3,9,15,21,\ldots}, r=3</math>; | + | :<math>K_3 = \left\{\ldots,-15,-9,-3,3,9,15,21,\ldots \right\}, r=3</math>; |
| − | :<math>K_4 = {\ldots,-14,-8,-2,4,10,16,22,\ldots}, r=4</math>; | + | :<math>K_4 = \left\{\ldots,-14,-8,-2,4,10,16,22,\ldots \right\}, r=4</math>; |
| − | :<math>K_5 = {\ldots,-13,-7,-1,5,11,17,23,\ldots}, r=5</math>, | + | :<math>K_5 = \left\{\ldots,-13,-7,-1,5,11,17,23,\ldots \right\}, r=5</math>, |
где через <math>r</math> обозначен остаток от деления целого числа на 6. | где через <math>r</math> обозначен остаток от деления целого числа на 6. | ||
| + | |||
| + | Напомним теорему о делении с остатком: | ||
| + | |||
| + | '''Теорема о делении с остатком''' | ||
| + | |||
| + | Для любых целых <math>a</math> и <math>b</math>, <math>b \not= 0</math>, существует единственный набор целых чисел <math>q</math> и <math>r</math>, что <math>a = bq + r</math> и <math>0 \le r < |b|</math>, где <math>|b|</math> — модуль числа <math>b</math>. | ||
| + | |||
| + | Легко доказывается, что для любых целых чисел <math>a</math> и <math>b</math>, <math>b \not= 0</math> деление с остатком возможно и числа <math>q</math> и <math>r</math> определяются однозначно. В нашем примере полная система наименьших неотрицательных вычетов есть множество <math>\left\{0, 1, 2, 3, 4, 5 \right\}</math>; полная система наименьших положительных вычетов – множество <math>\left\{0, 1, 2, 3, 4, 5, 6 \right\}</math>; полная система наименьших по абсолютной величине вычетов – множество <math>\left\{-2,-1, 0, 1, 2, 3 \right\}</math>; приведённая система вычетов – множество <math>\left\{1,5 \right\}</math>, так как <math>\phi(6) = 6\,\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right) = 2</math> ; фактор-множество <math>Z/{\equiv}_6 = \left\{K_0, K_1, K_2, K_3, K_4, K_5 \right\}</math>. | ||
Версия 13:07, 10 декабря 2014
Пример
Пусть модуль 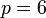 .
.
Тогда имеем шесть классов разбиения множества целых чисел по модулю 6:
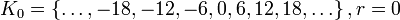 ;
;
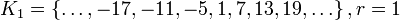 ;
;
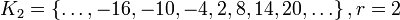 ;
;
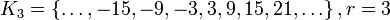 ;
;
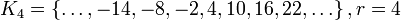 ;
;
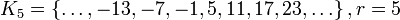 ,
,
где через  обозначен остаток от деления целого числа на 6.
обозначен остаток от деления целого числа на 6.
Напомним теорему о делении с остатком:
Теорема о делении с остатком
Для любых целых  и
и  ,
, 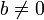 , существует единственный набор целых чисел
, существует единственный набор целых чисел 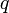 и
и  , что
, что 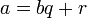 и
и 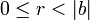 , где
, где 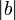 — модуль числа
— модуль числа  .
.
Легко доказывается, что для любых целых чисел  и
и  ,
, 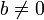 деление с остатком возможно и числа
деление с остатком возможно и числа 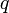 и
и  определяются однозначно. В нашем примере полная система наименьших неотрицательных вычетов есть множество
определяются однозначно. В нашем примере полная система наименьших неотрицательных вычетов есть множество 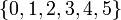 ; полная система наименьших положительных вычетов – множество
; полная система наименьших положительных вычетов – множество 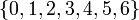 ; полная система наименьших по абсолютной величине вычетов – множество
; полная система наименьших по абсолютной величине вычетов – множество 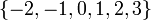 ; приведённая система вычетов – множество
; приведённая система вычетов – множество 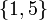 , так как
, так как 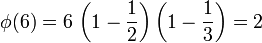 ; фактор-множество
; фактор-множество 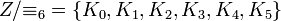 .
.