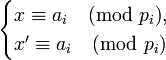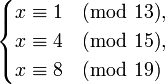Китайская теорема об остатках — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
Китайская теорема об остатках формулируется следующим образом: | Китайская теорема об остатках формулируется следующим образом: | ||
| − | Теорема. | + | '''Теорема'''. |
Пусть <math>p_1, p_2, \ldots, p_k</math> - попарно взаимно простые числа, большие 1, и пусть <math>P = p_1 \cdot p_2 \cdot \ldots \cdot p_k</math>. Тогда существует единственное неотрицательное решение по модулю <math>P</math> следующей системы сравнений: | Пусть <math>p_1, p_2, \ldots, p_k</math> - попарно взаимно простые числа, большие 1, и пусть <math>P = p_1 \cdot p_2 \cdot \ldots \cdot p_k</math>. Тогда существует единственное неотрицательное решение по модулю <math>P</math> следующей системы сравнений: | ||
: <math>x \equiv a_1 \pmod{p_1}</math>, | : <math>x \equiv a_1 \pmod{p_1}</math>, | ||
| − | : <math>x \equiv a_2 \pmod{p_2}</math>, | + | : <math>x \equiv a_2 \pmod{p_2}</math>, (*) |
| − | : <math>\ldots</math> | + | : <math>\ldots</math> |
: <math>x \equiv a_k \pmod{p_k}</math>. | : <math>x \equiv a_k \pmod{p_k}</math>. | ||
| − | Другими словами, отображение, которое каждому целому числу <math>x</math>, <math>0\le x <P</math>, ставит в соответствие кортеж <math>a_1, a_2, \ldots, a_k</math>, где <math>x \equiv a_i \pmod{p_i}, i = 1, \ldots k</math> является биекцией кольца <math>Z_P</math> на декартово произведение <math>Z_{p_1} \times Z_{p_2} \times \ldots \times Z_{p_k}</math> колец <math>Z_{p_1}, Z_{p_2}, \ldots, Z_{p_k}</math>. | + | Другими словами, отображение, которое каждому целому числу <math>x</math>, <math>0\le x <P</math>, ставит в соответствие кортеж <math>a_1, a_2, \ldots, a_k</math>, где <math>x \equiv a_i \pmod{p_i}, i = 1, \ldots k</math>, является биекцией кольца <math>Z_P</math> на декартово произведение <math>Z_{p_1} \times Z_{p_2} \times \ldots \times Z_{p_k}</math> колец <math>Z_{p_1}, Z_{p_2}, \ldots, Z_{p_k}</math>. |
| + | |||
Т.е. соответствие между числами и кортежами является взаимно однозначным, кроме того, операции, выполняемые над числом <math>a</math>, можно эквивалентно выполнять над соответствующими элементами кортежами путём независимого выполнения операций над каждым компонентом: | Т.е. соответствие между числами и кортежами является взаимно однозначным, кроме того, операции, выполняемые над числом <math>a</math>, можно эквивалентно выполнять над соответствующими элементами кортежами путём независимого выполнения операций над каждым компонентом: | ||
| Строка 32: | Строка 33: | ||
| − | Доказательство существования. | + | ''Доказательство существования.'' |
| − | Доказательство 1. | + | |
| + | ''Доказательство 1.'' | ||
Систему (*) можно решить так: | Систему (*) можно решить так: | ||
| − | (1) Для <math>i=1,\ldots, k</math> обозначим < | + | (1) Для <math>i=1,\ldots, k</math> обозначим <math>z_i=P/p_i=p_1\cdot p_2\cdot\ldots\cdot p_{i-1}\cdot p_{i+1}\cdot \ldots\cdot p_k</math>. |
| − | (2) Для <math>i=1,\ldots, k</math> обозначим < | + | (2) Для <math>i=1,\ldots, k</math> обозначим <math>y_i=z_{i}^{-1} \pmod{p_i}</math>. (Заметим, что это всегда можно сделать, поскольку <math>(z_i, p_i)=1</math>. |
(3) Решением системы является число <math>x=a_1\cdot y_1\cdot z_1 + \ldots +a_k\cdot y_k\cdot z_k=1</math>. | (3) Решением системы является число <math>x=a_1\cdot y_1\cdot z_1 + \ldots +a_k\cdot y_k\cdot z_k=1</math>. | ||
| − | Действительно, рассмотрим выражение для <math>x</math> и вычислим, например, <math>x \equiv a_1 \pmod{p_1}</math>. Заметим, что <math>z_i \equiv 0 \pmod{p_1}</math> при <math>i\ne 1</math> (это видно из выражения (1) для <math>z_i</math>). Таким образом, вычисляя <math>x \pmod{p_1}</math>, получаем <math>x \equiv a_1\cdot y_1\cdot z_1 \pmod{p_1}</math>. Но из определения < | + | |
| + | Действительно, рассмотрим выражение для <math>x</math> и вычислим, например, <math>x \equiv a_1 \pmod{p_1}</math>. Заметим, что <math>z_i \equiv 0 \pmod{p_1}</math> при <math>i\ne 1</math> (это видно из выражения (1) для <math>z_i</math>). Таким образом, вычисляя <math>x \pmod{p_1}</math>, получаем <math>x \equiv a_1\cdot y_1\cdot z_1 \pmod{p_1}</math>. Но из определения <math>y_i</math> (2) следует, что <math>y_1\cdot z_1 \equiv 1 \pmod{p_1}</math>, так что получаем <math>x \equiv a_1 \pmod{p_1}</math>. | ||
| + | |||
То же самое верно для других значений <math>i</math>. | То же самое верно для других значений <math>i</math>. | ||
| − | Существование решения доказано. | + | ''Существование решения доказано.'' |
| + | |||
| − | Доказательство 2. | + | ''Доказательство 2.'' |
Найдём число <math>x, 0\le x < P</math>, удовлетворяющее одновременно всем сравнениям, указанным в теореме. Систему сравнений будем решать присоединением на каждом шаге нового сравнения. Первое сравнение справедливо для всякого целого числа <math>x</math> вида | Найдём число <math>x, 0\le x < P</math>, удовлетворяющее одновременно всем сравнениям, указанным в теореме. Систему сравнений будем решать присоединением на каждом шаге нового сравнения. Первое сравнение справедливо для всякого целого числа <math>x</math> вида | ||
| Строка 76: | Строка 81: | ||
Применим теперь описанную процедуру к полученному сравнению и к одному из оставшихся сравнений исходной системы. Повторяя этот процесс <math>(k-1)</math> раз, мы в конечном итоге найдём число <math>x</math>, удовлетворяющее всем сравнениям исходной системы. | Применим теперь описанную процедуру к полученному сравнению и к одному из оставшихся сравнений исходной системы. Повторяя этот процесс <math>(k-1)</math> раз, мы в конечном итоге найдём число <math>x</math>, удовлетворяющее всем сравнениям исходной системы. | ||
| − | Существование решения доказано. | + | ''Существование решения доказано.'' |
| − | Доказательство единственности. | + | ''Доказательство единственности.'' |
Докажем единственность решения. Воспользуемся методом от противного. Предположим, что существует другое решение <math>x', 0\le x' < P</math> исходной системы. | Докажем единственность решения. Воспользуемся методом от противного. Предположим, что существует другое решение <math>x', 0\le x' < P</math> исходной системы. | ||
| Строка 92: | Строка 97: | ||
Вычитая почленно из первого сравнения второе, получим истинное сравнение <math>(x-x') \equiv 0 \pmod{p_i}</math>, | Вычитая почленно из первого сравнения второе, получим истинное сравнение <math>(x-x') \equiv 0 \pmod{p_i}</math>, | ||
| − | откуда следует, что для всех <math>i=1,\ldots,k</math> <math>(x-x')</math> делится нацело на <math>p_i</math>. Но тогда <math>(x-x')</math> делится нацело на <math> | + | откуда следует, что для всех <math>i=1,\ldots,k</math> выражение <math>(x-x')</math> делится нацело на <math>p_i</math>. Но тогда <math>(x-x')</math> делится нацело на <math>P</math>,следовательно, <math>x=x'</math>, так как <math>|x-x'|<P</math>. |
| + | |||
| + | ''Теорема доказана.'' | ||
| + | |||
| + | |||
| + | '''Пример.''' | ||
| + | |||
| + | Решим систему сравнений | ||
| + | |||
| + | :<math>\begin{cases}x \equiv 1 \pmod{13},\\ | ||
| + | x \equiv 4 \pmod{15},\\ | ||
| + | x \equiv 8 \pmod{19}\\ | ||
| + | \end{cases}</math> | ||
| + | |||
| + | |||
| + | ''Решение'' | ||
| + | |||
| + | Так как модули <math>13, 15, 19</math> попарно взаимно просты, то данная система имеет единственное решение по модулю <math>P = 13\cdot 15\cdot 19 = 3705</math>. Сравнение <math>x = 1 \pmod{13}</math> соответствует диофантову уравнению <math>x = 1 + 13\cdot t</math>, где <math>t \in Z</math>. | ||
| + | |||
| + | Заменяя <math>x</math> во втором сравнении системы на <math>1 + 13\cdot t</math>, получаем <math>1 + 13\cdot t \equiv 4 \pmod{15}</math>, т.е. <math>13\cdot t \equiv 3 \pmod{15}</math>. | ||
| + | |||
| + | К числу <math>13</math> обратным мультипликативным элементом по модулю <math>15</math> является число <math>7</math>. Умножая последнее сравнение на <math>7</math> и переходя в нём к вычетам по модулю 15, получим <math>t \equiv 6 \pmod{15}</math>. Таким образом, <math>t = 6 + 15\cdot u</math>, где <math>u \in Z</math>. | ||
| + | |||
| + | Следовательно, <math>x = 1 + 13\cdot t = 1+13 \cdot (6 + 15 \cdot u) = 79 + 195 \cdot u</math>, при этом все числа вида <math>x = 79 + 195 \cdot u, u \in Z</math> являются решениями первых двух сравнений данной системы. | ||
| + | |||
| + | Подставим в третье сравнение вместо <math>x</math> полученное выше значение <math>79 + 195 \cdot u</math>: | ||
| + | |||
| + | :<math>79 + 195 \cdot u \equiv 8 \pmod{19}</math>, | ||
| + | или (переносим <math>79</math>) | ||
| + | :<math>195 \cdot u \equiv 5 \pmod{19}</math>, | ||
| + | далее (делим обе части на <math>5</math>) | ||
| + | :<math>39 \cdot u \equiv 1 \pmod{19}</math>. | ||
| + | |||
| + | Так как <math>(39, 19) = 1</math>, то <math>u \equiv 1 \pmod{19}</math>, или <math>u = 1 + 19 \cdot v, v \in Z</math>. | ||
| + | |||
| + | Итак, | ||
| − | + | :<math>79 + 195 \cdot u = 79 + 195 \cdot (1 + 19 \cdot v) = 274 + 3705 \cdot v</math>, т.е. <math>x = 274</math>. | |
Текущая версия на 09:51, 4 февраля 2015
Китайская теорема об остатках формулируется следующим образом:
Теорема.
Пусть 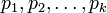 - попарно взаимно простые числа, большие 1, и пусть
- попарно взаимно простые числа, большие 1, и пусть 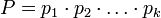 . Тогда существует единственное неотрицательное решение по модулю
. Тогда существует единственное неотрицательное решение по модулю 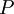 следующей системы сравнений:
следующей системы сравнений:
-
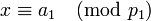 ,
,
-
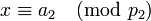 , (*)
, (*)
-
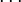
-
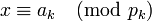 .
.
Другими словами, отображение, которое каждому целому числу  ,
, 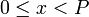 , ставит в соответствие кортеж
, ставит в соответствие кортеж 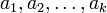 , где
, где 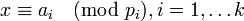 , является биекцией кольца
, является биекцией кольца 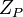 на декартово произведение
на декартово произведение 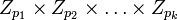 колец
колец 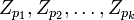 .
.
Т.е. соответствие между числами и кортежами является взаимно однозначным, кроме того, операции, выполняемые над числом  , можно эквивалентно выполнять над соответствующими элементами кортежами путём независимого выполнения операций над каждым компонентом:
, можно эквивалентно выполнять над соответствующими элементами кортежами путём независимого выполнения операций над каждым компонентом:
если
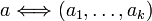 ,
,
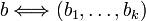 ,
,
то справедливо:
-
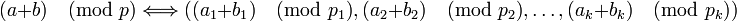 ,
,
-
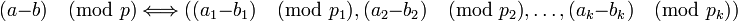 ,
,
-
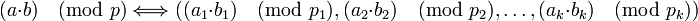 .
.
Существует много различных доказательств китайской теоремы об остатках. Приведём конструктивное доказательство этой теоремы.
Доказательство существования.
Доказательство 1.
Систему (*) можно решить так:
(1) Для 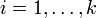 обозначим
обозначим 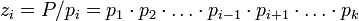 .
.
(2) Для 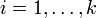 обозначим
обозначим 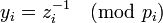 . (Заметим, что это всегда можно сделать, поскольку
. (Заметим, что это всегда можно сделать, поскольку 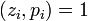 .
.
(3) Решением системы является число 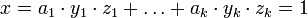 .
.
Действительно, рассмотрим выражение для  и вычислим, например,
и вычислим, например, 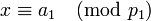 . Заметим, что
. Заметим, что 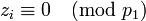 при
при 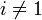 (это видно из выражения (1) для
(это видно из выражения (1) для 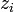 ). Таким образом, вычисляя
). Таким образом, вычисляя 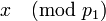 , получаем
, получаем 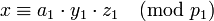 . Но из определения
. Но из определения 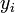 (2) следует, что
(2) следует, что 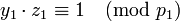 , так что получаем
, так что получаем 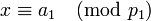 .
.
То же самое верно для других значений 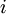 .
.
Существование решения доказано.
Доказательство 2.
Найдём число 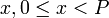 , удовлетворяющее одновременно всем сравнениям, указанным в теореме. Систему сравнений будем решать присоединением на каждом шаге нового сравнения. Первое сравнение справедливо для всякого целого числа
, удовлетворяющее одновременно всем сравнениям, указанным в теореме. Систему сравнений будем решать присоединением на каждом шаге нового сравнения. Первое сравнение справедливо для всякого целого числа  вида
вида
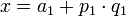 , где
, где 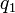 - произвольное целое число.
- произвольное целое число.
Для нахождения 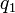 подставим значение
подставим значение  во второе сравнение системы,
после чего получим
во второе сравнение системы,
после чего получим 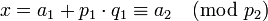 ,
откуда
,
откуда 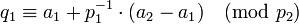 ,
,
где 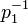 - обратный мультипликативный элемент к
- обратный мультипликативный элемент к 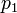 по модулю
по модулю 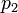 .
Такой элемент существует, так как
.
Такой элемент существует, так как 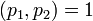 .
.
Найденное таким образом 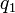 можно записать в виде
можно записать в виде
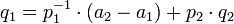
для некоторого целого числа 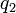 .
.
Подставим значение 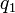 в выражение
в выражение
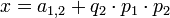 .
.
Теперь первые два сравнения могут быть заменены на одно
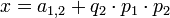 .
.
Применим теперь описанную процедуру к полученному сравнению и к одному из оставшихся сравнений исходной системы. Повторяя этот процесс 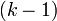 раз, мы в конечном итоге найдём число
раз, мы в конечном итоге найдём число  , удовлетворяющее всем сравнениям исходной системы.
, удовлетворяющее всем сравнениям исходной системы.
Существование решения доказано.
Доказательство единственности.
Докажем единственность решения. Воспользуемся методом от противного. Предположим, что существует другое решение 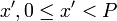 исходной системы.
исходной системы.
Тогда
для всех 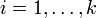 .
.
Вычитая почленно из первого сравнения второе, получим истинное сравнение 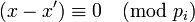 ,
откуда следует, что для всех
,
откуда следует, что для всех 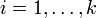 выражение
выражение 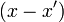 делится нацело на
делится нацело на 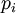 . Но тогда
. Но тогда 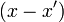 делится нацело на
делится нацело на 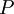 ,следовательно,
,следовательно, 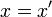 , так как
, так как 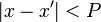 .
.
Теорема доказана.
Пример.
Решим систему сравнений
Решение
Так как модули 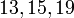 попарно взаимно просты, то данная система имеет единственное решение по модулю
попарно взаимно просты, то данная система имеет единственное решение по модулю 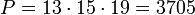 . Сравнение
. Сравнение 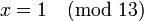 соответствует диофантову уравнению
соответствует диофантову уравнению 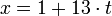 , где
, где 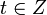 .
.
Заменяя  во втором сравнении системы на
во втором сравнении системы на 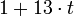 , получаем
, получаем 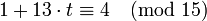 , т.е.
, т.е.  .
.
К числу 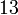 обратным мультипликативным элементом по модулю
обратным мультипликативным элементом по модулю 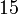 является число
является число 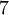 . Умножая последнее сравнение на
. Умножая последнее сравнение на 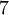 и переходя в нём к вычетам по модулю 15, получим
и переходя в нём к вычетам по модулю 15, получим 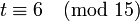 . Таким образом,
. Таким образом, 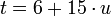 , где
, где 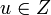 .
.
Следовательно, 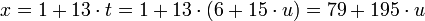 , при этом все числа вида
, при этом все числа вида 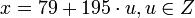 являются решениями первых двух сравнений данной системы.
являются решениями первых двух сравнений данной системы.
Подставим в третье сравнение вместо  полученное выше значение
полученное выше значение 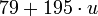 :
:
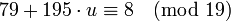 ,
,
или (переносим 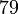 )
)
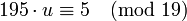 ,
,
далее (делим обе части на 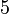 )
)
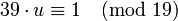 .
.
Так как 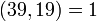 , то
, то 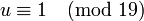 , или
, или 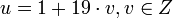 .
.
Итак,
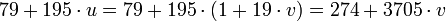 , т.е.
, т.е. 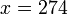 .
.