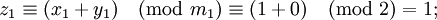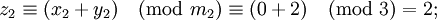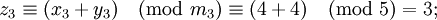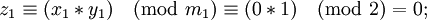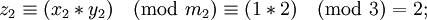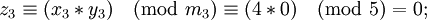Система остаточных классов — различия между версиями
Bundin (обсуждение | вклад) (→Основные определения) |
Turbo (обсуждение | вклад) |
||
| (не показано 19 промежуточных версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Система остаточных классов | + | '''Система остаточных классов (СОК)''' (от англ. [http://en.wikipedia.org/wiki/Residue_number_system Residue number system], другое название '''Модулярная арифметика''') - [http://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F#.D0.9D.D0.B5.D0.BF.D0.BE.D0.B7.D0.B8.D1.86.D0.B8.D0.BE.D0.BD.D0.BD.D1.8B.D0.B5_.D1.81.D0.B8.D1.81.D1.82.D0.B5.D0.BC.D1.8B_.D1.81.D1.87.D0.B8.D1.81.D0.BB.D0.B5.D0.BD.D0.B8.D1.8F непозиционная система счисления]. Представление числа в системе остаточных классов основано на понятии [http://ru.wikipedia.org/wiki/%D0%A1%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BF%D0%BE_%D0%BC%D0%BE%D0%B4%D1%83%D0%BB%D1%8E вычета] и [http://ru.wikipedia.org/wiki/%D0%9A%D0%B8%D1%82%D0%B0%D0%B9%D1%81%D0%BA%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%BE%D0%B1_%D0%BE%D1%81%D1%82%D0%B0%D1%82%D0%BA%D0%B0%D1%85 китайской теореме об остатках]. СОК определяется набором [http://ru.wikipedia.org/wiki/%D0%92%D0%B7%D0%B0%D0%B8%D0%BC%D0%BD%D0%BE_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%8B%D0%B5_%D1%87%D0%B8%D1%81%D0%BB%D0%B0 взаимно простых] ''модулей'' <math>(m_1, m_2, \dots, m_n)</math> с произведением <math>M=m_1\cdot m_2\cdot \dots\cdot m_n</math> так, что каждому целому числу <math>x</math> из отрезка <math>[0,M-1]</math> ставится в соответствие набор вычетов <math>(x_1, x_2, \dots, x_n)</math>, где |
| + | : <math>x_1 \equiv x \pmod{m_1};</math> | ||
| + | : <math>x_2 \equiv x \pmod{m_2};</math> | ||
| + | : … | ||
| + | : <math>x_n \equiv x \pmod{m_n}.</math> | ||
| + | При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка <math>[0,M-1]</math>. | ||
| − | == | + | == Преимущества системы остаточных классов == |
| − | + | * В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в <math>[0,M-1]</math>. | |
| + | Формула для сложения: | ||
| + | <math>(x_1, x_2, \dots, x_n) + (y_1, y_2, \dots, y_n) = (z_1, z_2, \dots, z_n)</math>, где | ||
| + | : <math>z_1 \equiv (x_1 + y_1) \pmod{m_1};</math> | ||
| + | : <math>z_2 \equiv (x_2 + y_2) \pmod{m_2};</math> | ||
| + | : ... | ||
| + | : <math>z_n \equiv (x_n + y_n) \pmod{m_n};</math> | ||
| + | Аналогично выполняются вычитание, умножение и деление. | ||
| + | '''Замечание''': на деление накладываются дополнительные ограничения: деление должно быть целочисленным, то есть делитель должен нацело делить делимое. Делитель должен быть взаимопростым со всеми модулями базиса. | ||
| − | == | + | == Недостатки системы остаточных классов == |
| − | + | * Возможность представления только ограниченного количества чисел. | |
| + | * Отсутствие эффективных алгоритмов для сравнения чисел, представленных в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям <math>(m_1, m_1\cdot m_2, \dots, m_1\cdot m_2\cdot\dots\cdot m_{n-1})</math>. | ||
| + | * Медленные и требующие работы с большими числами реализации алгоритмов перевода из позиционной системы счисления в СОК и обратно. | ||
| + | * Сложные алгоритмы деления (для случая, когда результат не является целым) | ||
| + | * Трудность в обнаружении переполнения | ||
| − | == | + | == Применение системы остаточных классов == |
| − | + | СОК широко используется в микроэлектронике в специализированных устройствах [ЦОС], где требуется: | |
| + | * контроль за ошибками, за счет введения дополнительных избыточных модулей | ||
| + | * высокая скорость работы, которую обеспечивает параллельная реализация базовых арифметических операций | ||
| − | == | + | == Специальные системы модулей == |
| − | < | + | В модулярной арифметике существуют специальные наборы модулей, которые позволяют частично нивелировать недостатки и для которых существуют эффективные алгоритмы сравнения чисел и для прямого и обратного перевода модулярных чисел в позиционную систему счисления. Одной из самых популярных систем модулей является набор из трех взаимнопростых чисел вида '''{2<sup>n</sup>-1, 2<sup>n</sup>, 2<sup>n</sup>+1}''' |
| − | === | + | == Численный пример == |
| − | + | ||
| − | == | + | == Пример == |
| − | + | ||
| + | Рассмотрим СОК с базисом <math>(2;3;5)</math>. В этом базисе можно взаимооднозначно представить числа из промежутка от <math>0</math> до <math>29</math>, так как <math>M = 2\times 3\times 5 = 30</math>. Таблица соответствия чисел из позиционной системы счисления и системы остаточных классов: | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | <math>0=(0;0;0)</math> || <math>1=(1;1;1)</math> || <math>2=(0;2;2)</math> || <math>3=(1;0;3)</math> || <math>4=(0;1;4)</math> | ||
| + | |- | ||
| + | | <math>5=(1;2;0)</math> || <math>6=(0;0;1)</math> || <math>7=(1;1;2)</math> || <math>8=(0;2;3)</math> || <math>9=(1;0;4)</math> | ||
| + | |- | ||
| + | | <math>10=(0;1;0)</math> || <math>11=(1;2;1)</math> || <math>12=(0;0;2)</math> || <math>13=(1;1;3)</math> || <math>14=(0;2;4)</math> | ||
| + | |- | ||
| + | | <math>15=(1;0;0)</math> || <math>16=(0;1;1)</math> || <math>17=(1;2;2)</math> || <math>18=(0;0;3)</math> || <math>19=(1;1;4)</math> | ||
| + | |- | ||
| + | | <math>20=(0;2;0)</math> || <math>21=(1;0;1)</math> || <math>22=(0;1;2)</math> || <math>23=(1;2;3)</math> || <math>24=(0;0;4)</math> | ||
| + | |- | ||
| + | | <math>25=(1;1;0)</math> || <math>26=(0;2;1)</math> || <math>27=(1;0;2)</math> || <math>28=(0;1;3)</math> || <math>29=(1;2;4)</math> | ||
| + | |} | ||
| + | === Пример сложения === | ||
| + | Сложим два числа 9 и 14 в базисе <math>(2;3;5)</math>. Их представление в заданном базисе <math>9=(1;0;4)</math> и <math>14=(0;2;4)</math> (см. табличку выше). Воспользуемся формулой для сложения: | ||
| + | <math>(z_1, z_2, z_3) = (1, 0, 4) + (0, 2, 4)</math> | ||
| + | : <math>z_1 \equiv (x_1 + y_1) \pmod{m_1} \equiv (1 + 0) \pmod{2} = 1;</math> | ||
| + | : <math>z_2 \equiv (x_2 + y_2) \pmod{m_2} \equiv (0 + 2) \pmod{3} = 2;</math> | ||
| + | : <math>z_3 \equiv (x_3 + y_3) \pmod{m_3} \equiv (4 + 4) \pmod{5} = 3;</math> | ||
| + | <math>(z_1, z_2, z_3) = (1, 2, 3)</math> - по таблице убеждаемся, что результат равен 23. | ||
| − | == | + | === Пример умножения === |
| − | + | Умножим два числа 4 и 5 в базисе <math>(2;3;5)</math>. Их представление в заданном базисе <math>4=(0;1;4)</math> и <math>5=(1;2;0)</math> (см. табличку выше). Воспользуемся формулой для умножения: | |
| − | + | <math>(z_1, z_2, z_3) = (0, 1, 4) * (1, 2, 0)</math> | |
| − | + | : <math>z_1 \equiv (x_1 * y_1) \pmod{m_1} \equiv (0 * 1) \pmod{2} = 0;</math> | |
| − | + | : <math>z_2 \equiv (x_2 * y_2) \pmod{m_2} \equiv (1 * 2) \pmod{3} = 2;</math> | |
| − | + | : <math>z_3 \equiv (x_3 * y_3) \pmod{m_3} \equiv (4 * 0) \pmod{5} = 0;</math> | |
| − | + | <math>(z_1, z_2, z_3) = (0, 2, 0)</math> - по таблице убеждаемся, что результат равен 20. | |
| − | + | ||
| − | + | Замечание: если бы мы умножали или складывали числа, которые дали в результате умножения число больше или равное <math>M = 30</math>, то полученный результат <math>RES \equiv REAL \pmod{M}</math>, где <math>REAL</math> - результат операции в позиционной системе счисления. | |
| − | + | ||
| − | + | === Пример деления, при условии, что оно делится нацело === | |
| − | + | Деление может быть выполнено аналогично умножению, но только если делитель делит делимое нацело, без остатка. | |
| − | + | <br /> | |
| − | + | Для модулей <math>(29;31;32)</math> разделим число 1872 на 9.<br /> | |
| − | + | Делим <math>1872=(16;12;16)</math> на <math>9=(9;9;9)</math>.<br /> | |
| − | + | ||
| − | + | Воспользуемся формулой<br /> | |
| − | }} | + | <math>z_i \equiv (x_i * y_i^{-1}) \pmod{m_i};</math> |
| + | <br /><br /> | ||
| + | Здесь надо сказать, что <math>y_i^{-1}*y_i=1 \pmod{m_i}</math>, что не то же самое, что просто разделить x на y.<br /> | ||
| + | По формуле <math>y_i^{m_i-1}=1 \pmod{m_i}</math> получаем<br /> | ||
| + | <math>9^{29-2} \pmod{29} = 13</math><br /> | ||
| + | <math>9^{31-2} \pmod{31} = 7</math><br /> | ||
| + | <math>9^{32-2} \pmod{32} = 17</math><br /> | ||
| + | |||
| + | |||
| + | <math>z_1 \equiv (16*13) \pmod{29} = 5</math><br /> | ||
| + | <math>z_2 \equiv (12*7) \pmod{31} = 22</math><br /> | ||
| + | <math>z_3 \equiv (16*17) \pmod{32} = 16</math><br /> | ||
| + | <br /> | ||
| + | Это и есть правильный результат - число 208. Однако такой результат можно получить только если известно, что деление производится без остатка. | ||
| + | |||
| + | == Ссылки == | ||
| + | * Книга "Residue Number Systems: Theory and Implementation", Amos Omondi, Benjamin Premkumar - наиболее исчерпывающая информация о применении СОК с подробными примерами (на английском языке). | ||
Текущая версия на 09:07, 21 декабря 2015
Система остаточных классов (СОК) (от англ. Residue number system, другое название Модулярная арифметика) - непозиционная система счисления. Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором взаимно простых модулей 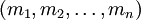 с произведением
с произведением 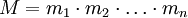 так, что каждому целому числу
так, что каждому целому числу  из отрезка
из отрезка ![[0,M-1]](/w/images/math/5/6/5/56591240ff770cb9db7f3205c6befa98.png) ставится в соответствие набор вычетов
ставится в соответствие набор вычетов 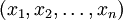 , где
, где
-
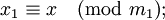
-
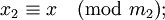
- …
-
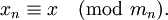
При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка ![[0,M-1]](/w/images/math/5/6/5/56591240ff770cb9db7f3205c6befa98.png) .
.
Содержание
Преимущества системы остаточных классов
- В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в
![[0,M-1]](/w/images/math/5/6/5/56591240ff770cb9db7f3205c6befa98.png) .
.
Формула для сложения:
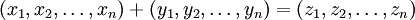 , где
, где
-
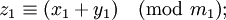
-
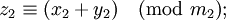
- ...
-
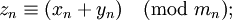
Аналогично выполняются вычитание, умножение и деление. Замечание: на деление накладываются дополнительные ограничения: деление должно быть целочисленным, то есть делитель должен нацело делить делимое. Делитель должен быть взаимопростым со всеми модулями базиса.
Недостатки системы остаточных классов
- Возможность представления только ограниченного количества чисел.
- Отсутствие эффективных алгоритмов для сравнения чисел, представленных в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям
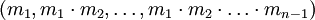 .
.
- Медленные и требующие работы с большими числами реализации алгоритмов перевода из позиционной системы счисления в СОК и обратно.
- Сложные алгоритмы деления (для случая, когда результат не является целым)
- Трудность в обнаружении переполнения
Применение системы остаточных классов
СОК широко используется в микроэлектронике в специализированных устройствах [ЦОС], где требуется:
- контроль за ошибками, за счет введения дополнительных избыточных модулей
- высокая скорость работы, которую обеспечивает параллельная реализация базовых арифметических операций
Специальные системы модулей
В модулярной арифметике существуют специальные наборы модулей, которые позволяют частично нивелировать недостатки и для которых существуют эффективные алгоритмы сравнения чисел и для прямого и обратного перевода модулярных чисел в позиционную систему счисления. Одной из самых популярных систем модулей является набор из трех взаимнопростых чисел вида {2n-1, 2n, 2n+1}
Численный пример
Пример
Рассмотрим СОК с базисом 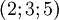 . В этом базисе можно взаимооднозначно представить числа из промежутка от
. В этом базисе можно взаимооднозначно представить числа из промежутка от 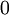 до
до 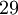 , так как
, так как 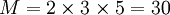 . Таблица соответствия чисел из позиционной системы счисления и системы остаточных классов:
. Таблица соответствия чисел из позиционной системы счисления и системы остаточных классов:
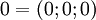 |
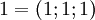 |
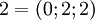 |
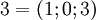 |
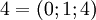
|
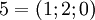 |
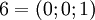 |
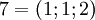 |
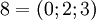 |
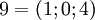
|
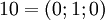 |
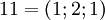 |
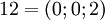 |
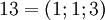 |
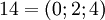
|
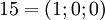 |
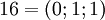 |
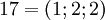 |
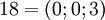 |
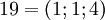
|
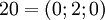 |
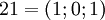 |
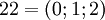 |
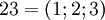 |
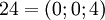
|
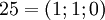 |
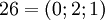 |
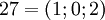 |
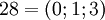 |
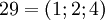
|
Пример сложения
Сложим два числа 9 и 14 в базисе 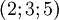 . Их представление в заданном базисе
. Их представление в заданном базисе 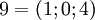 и
и 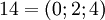 (см. табличку выше). Воспользуемся формулой для сложения:
(см. табличку выше). Воспользуемся формулой для сложения:
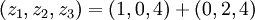
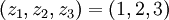 - по таблице убеждаемся, что результат равен 23.
- по таблице убеждаемся, что результат равен 23.
Пример умножения
Умножим два числа 4 и 5 в базисе 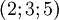 . Их представление в заданном базисе
. Их представление в заданном базисе 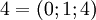 и
и 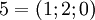 (см. табличку выше). Воспользуемся формулой для умножения:
(см. табличку выше). Воспользуемся формулой для умножения:
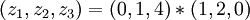
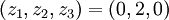 - по таблице убеждаемся, что результат равен 20.
- по таблице убеждаемся, что результат равен 20.
Замечание: если бы мы умножали или складывали числа, которые дали в результате умножения число больше или равное 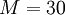 , то полученный результат
, то полученный результат 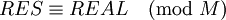 , где
, где 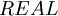 - результат операции в позиционной системе счисления.
- результат операции в позиционной системе счисления.
Пример деления, при условии, что оно делится нацело
Деление может быть выполнено аналогично умножению, но только если делитель делит делимое нацело, без остатка.
Для модулей 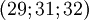 разделим число 1872 на 9.
разделим число 1872 на 9.
Делим 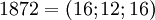 на
на 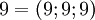 .
.
Воспользуемся формулой
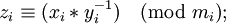
Здесь надо сказать, что 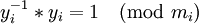 , что не то же самое, что просто разделить x на y.
, что не то же самое, что просто разделить x на y.
По формуле 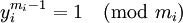 получаем
получаем
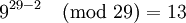
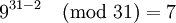
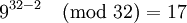

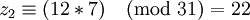
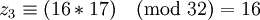
Это и есть правильный результат - число 208. Однако такой результат можно получить только если известно, что деление производится без остатка.
Ссылки
- Книга "Residue Number Systems: Theory and Implementation", Amos Omondi, Benjamin Premkumar - наиболее исчерпывающая информация о применении СОК с подробными примерами (на английском языке).