Вычет по комплексному модулю — различия между версиями
Материал из Модулярная арифметики
Turbo (обсуждение | вклад) |
DimaT (обсуждение | вклад) (→Вычет комплексного числа по комплексному переменному) |
||
| Строка 10: | Строка 10: | ||
<math>|x|_p</math> - в данном равенстве и есть вычет. | <math>|x|_p</math> - в данном равенстве и есть вычет. | ||
| − | == | + | == Китайская теорема об остатках "второй версии" == |
| − | + | По сути, КТО II есть ни что иное как видоизмененный обратный преобразователь на базе перевода в полиадический код. Вся суть состоит в структуризации данных. КТО II использует известный подход под названием divide and conquer. Аналогичный подход используется в БПФ преобразованиях. | |
| − | + | Базовой процедурой, необходимой для описания КТО II является процедура восстановления числа по двум остаткам. Обозначим модули как <math>m_1, m_2</math> и вычеты <math>x_1, x_2</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <math> | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Версия 10:45, 5 апреля 2013
По аналогии с вычетом целого числа по целому числу, можно определить вычет для комплексных переменных.
Вычет целого числа по целому переменному
Пусть заданы два целых положительных числа 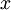 и
и 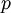 .
Справедливо равенство:
.
Справедливо равенство: 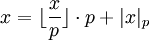 .
.
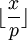 - наибольшее целое число от деления
- наибольшее целое число от деления 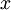 на
на 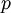 .
.
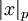 - в данном равенстве и есть вычет.
- в данном равенстве и есть вычет.
Китайская теорема об остатках "второй версии"
По сути, КТО II есть ни что иное как видоизмененный обратный преобразователь на базе перевода в полиадический код. Вся суть состоит в структуризации данных. КТО II использует известный подход под названием divide and conquer. Аналогичный подход используется в БПФ преобразованиях.
Базовой процедурой, необходимой для описания КТО II является процедура восстановления числа по двум остаткам. Обозначим модули как 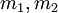 и вычеты
и вычеты