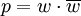Вычет по комплексному модулю — различия между версиями
Материал из Модулярная арифметики
Turbo (обсуждение | вклад) (Новая страница: «По аналогии с вычетом целого числа по целому числу, можно определить вычет для комплексн…») |
Turbo (обсуждение | вклад) м (Turbo переименовал страницу Вычет по комплексному переменному в Вычет по комплексному модулю) |
||
| (не показано 6 промежуточных версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
По аналогии с вычетом целого числа по целому числу, можно определить вычет для комплексных переменных. | По аналогии с вычетом целого числа по целому числу, можно определить вычет для комплексных переменных. | ||
| + | |||
| + | == Вычет целого числа по целому модулю == | ||
| + | |||
| + | Пусть заданы два целых положительных числа <math>{x}</math> и <math>{p}</math>. | ||
| + | Справедливо равенство: <math>x = \lfloor\frac{x}{p}\rfloor\cdot{p} + |x|_p</math>. | ||
| + | |||
| + | <math>\lfloor\frac{x}{p}\rfloor</math> - наибольшее целое число от деления <math>{x}</math> на <math>{p}</math>. | ||
| + | |||
| + | <math>|x|_p</math> - в данном равенстве и есть вычет. | ||
| + | |||
| + | == Вычет комплексного числа по комплексному модулю == | ||
| + | |||
| + | Пусть <math>w</math> – фиксированное целое комплексное число <math>w=a+bj\in{CZ}</math> с нормой <math>p=a^2+b^2</math>. Пусть <math>z=x+yj</math> – произвольное целое комплексное число. | ||
| + | |||
| + | Проведем следующие преобразования: | ||
| + | <math>z = \frac{z\cdot{p}}{p} = \frac{z\cdot{w}\cdot{\overline{w}}}{p} = \frac{z\cdot{\overline{w}}}{p}\cdot {w} = \frac{\lfloor\frac{z\cdot{\overline{w}}}{p}\rfloor\cdot{p} + |{z}\cdot{\overline{w}}|_p}{p}\cdot{w} = \lfloor\frac{z\cdot{\overline{w}}}{p}\rfloor + \frac{|{z}\cdot{\overline{w}}|_p\cdot{w}}{p}</math> | ||
| + | |||
| + | Назовем второй член получившегося выражения вычетом комплексного числа по комплексному переменному и обозначим: | ||
| + | |||
| + | <math>\langle{z}|_w = \frac{|{z}\cdot{\overline{w}}|_p\cdot{w}}{p}</math> | ||
| + | |||
| + | Для преобразований используются следующий свойства: | ||
| + | * <math>\overline{w} = a-bj</math> - сопряженное к <math>{w}</math> комплексное число. | ||
| + | * <math>p = {w}\cdot{\overline{w}}</math> | ||
Текущая версия на 09:09, 10 апреля 2013
По аналогии с вычетом целого числа по целому числу, можно определить вычет для комплексных переменных.
Вычет целого числа по целому модулю
Пусть заданы два целых положительных числа 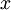 и
и 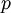 .
Справедливо равенство:
.
Справедливо равенство: 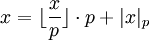 .
.
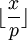 - наибольшее целое число от деления
- наибольшее целое число от деления 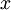 на
на 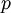 .
.
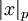 - в данном равенстве и есть вычет.
- в данном равенстве и есть вычет.
Вычет комплексного числа по комплексному модулю
Пусть 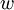 – фиксированное целое комплексное число
– фиксированное целое комплексное число 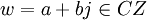 с нормой
с нормой 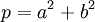 . Пусть
. Пусть 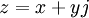 – произвольное целое комплексное число.
– произвольное целое комплексное число.
Проведем следующие преобразования:
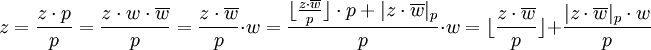
Назовем второй член получившегося выражения вычетом комплексного числа по комплексному переменному и обозначим:
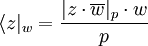
Для преобразований используются следующий свойства:
-
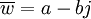 - сопряженное к
- сопряженное к 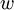 комплексное число.
комплексное число.
-