Сравнение разных методов умножения по модулю — различия между версиями
Материал из Модулярная арифметики
| Строка 216: | Строка 216: | ||
== Результаты == | == Результаты == | ||
Выводы: | Выводы: | ||
| − | + | #Наиболее предпочтительным является использование умножителей, использующих метод разности квадратов. | |
| − | + | #Самым неэффективным оказался индексный умножитель. | |
| − | + | #У DS-умножителя наблюдается аномальный скачок всех трёх параметров для 3-битных чисел. | |
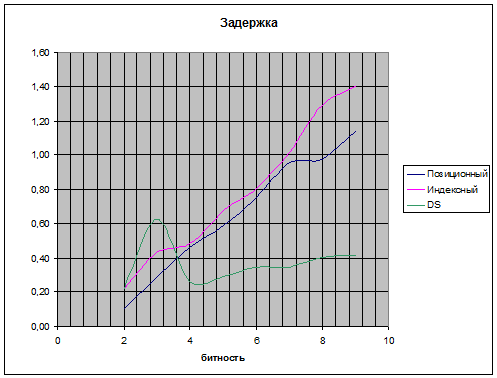
[[Изображение:delay.png]] | [[Изображение:delay.png]] | ||
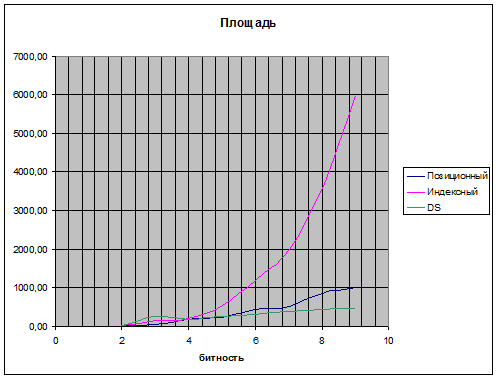
[[Изображение:area.png]] | [[Изображение:area.png]] | ||
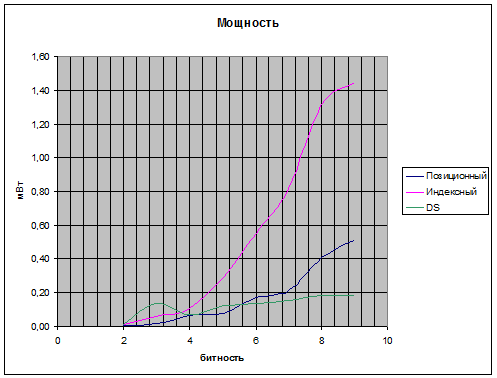
[[Изображение:power.png]] | [[Изображение:power.png]] | ||
* [http://vscripts.ru/res/files/Graph-Std-Multiplication.xlsx Скачать Excel-файл с численными данными] | * [http://vscripts.ru/res/files/Graph-Std-Multiplication.xlsx Скачать Excel-файл с численными данными] | ||
Версия 06:52, 26 декабря 2012
Было произведено сравнение позиционного, индексного умножителя и умножителя по методу разности квадратов (далее DS-умножитель). Сравнение производилось для чисел с разрядность от 2 до 9 бит. Запуск производился на Synopsys Design Compiler.
Содержание
Типовые Verilog-модули
1.Позиционный умножитель
module dif_multipliers_12_12 (a,b,out); output wire [23:0] out; input wire [11:0] a,b; assign out=a*b; endmodule
2. Индексный умножитель
module multiplication_mod_3(inp1, inp2, out); input [1:0] inp1; input [1:0] inp2; output reg [1:0] out; wire [1:0] out_pre; wire [1:0] w_1_0; wire [1:0] w_2_0; wire [1:0] wout_0; lut_input_3 lut1(inp1, w_1_0); lut_input_3 lut2(inp2, w_2_0); sum_modulo_2 sm0(w_1_0, w_2_0, wout_0); lut_output_3 lut3(wout_0, out_pre); always @ (*) begin if (inp1 == 0 || inp2 == 0) begin out = 0; end else begin out = out_pre; end end endmodule module sum_modulo_2(inp1, inp2, out); input [1:0] inp1; input [1:0] inp2; output reg [1:0] out; wire [2:0] int; assign int = inp1 + inp2; always @ (*) begin if (int < 2) begin out = int; end else begin out = int - 2; end end endmodule module lut_output_3(inp0, out); output reg [1:0] out; input [1:0] inp0; always @ (*) begin if (inp0 == 0) begin out <= 1; end else if (inp0 == 1) begin out <= 2; end else begin out <= 0; end end endmodule module lut_input_3(inp, out0); input [1:0] inp; output reg [1:0] out0; always @ (inp) begin case(inp) 1: begin out0 <= 0; end 2: begin out0 <= 1; end default: begin out0 <= 0; end endcase end endmodule
3.DS-умножитель
module multiplication_mod_3(inp1, inp2, out); input [1:0] inp1; input [1:0] inp2; output reg [1:0] out; wire [1:0] out_pre; wire [1:0] w_1_0; wire [1:0] w_2_0; wire [1:0] wout_0; lut_input_3 lut1(inp1, w_1_0); lut_input_3 lut2(inp2, w_2_0); sum_modulo_2 sm0(w_1_0, w_2_0, wout_0); lut_output_3 lut3(wout_0, out_pre); always @ (*) begin if (inp1 == 0 || inp2 == 0) begin out = 0; end else begin out = out_pre; end end endmodule module sum_modulo_2(inp1, inp2, out); input [1:0] inp1; input [1:0] inp2; output reg [1:0] out; wire [2:0] int; assign int = inp1 + inp2; always @ (*) begin if (int < 2) begin out = int; end else begin out = int - 2; end end endmodule module lut_output_3(inp0, out); output reg [1:0] out; input [1:0] inp0; always @ (*) begin if (inp0 == 0) begin out <= 1; end else if (inp0 == 1) begin out <= 2; end else begin out <= 0; end end endmodule module lut_input_3(inp, out0); input [1:0] inp; output reg [1:0] out0; always @ (inp) begin case(inp) 1: begin out0 <= 0; end 2: begin out0 <= 1; end default: begin out0 <= 0; end endcase end endmodule
Библиотека стандартных ячеек
NangateOpenCellLibrary_typical_conditional_nldm.lib
Скрипт для запуска
analyze -f verilog <имя модуля>.v elaborate <имя модуля> uniquify current_design <имя модуля> check_design set_load [load_of [get_lib_pins NangateOpenCellLibrary/INV_X4/A]] [all_outputs] set_driving_cell -lib_cell DFFRS_X2 -library NangateOpenCellLibrary -pin Q [all_inputs] set_max_delay -to [all_outputs] 0 set_max_area 0 compile report_timing -significant_digits 6 > timing_<имя модуля>.rpt report_area > area_<имя модуля>.rpt report_power -analysis_effort high > power_<имя модуля>.rpt remove_design
Результаты
Выводы:
- Наиболее предпочтительным является использование умножителей, использующих метод разности квадратов.
- Самым неэффективным оказался индексный умножитель.
- У DS-умножителя наблюдается аномальный скачок всех трёх параметров для 3-битных чисел.