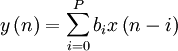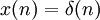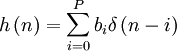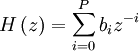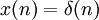Фильтр с конечной импульсной характеристикой — различия между версиями

Материал из Модулярная арифметики
Перейти к: навигация, поиск
 
(не показана одна промежуточная версия этого же участника)
Строка 21: Строка 21:
 
== Прямая форма КИХ фильтра ==
 
== Прямая форма КИХ фильтра ==
 
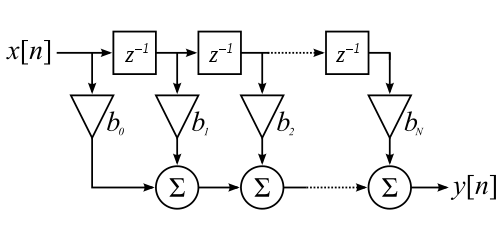
КИХ фильтры могут быть реализованы с использованием трех элементов: умножитель, сумматор и блок задержки. Вариант, показанный на рисунке, есть прямая реализация КИХ-фильтров типа 1.
 
КИХ фильтры могут быть реализованы с использованием трех элементов: умножитель, сумматор и блок задержки. Вариант, показанный на рисунке, есть прямая реализация КИХ-фильтров типа 1.
−
[[Файл:FIR Filter.png|center|thumb|Реализация прямой формы КИХ фильтра]]
+
[[Файл:FIR Filter.png|center|Реализация прямой формы КИХ фильтра]]
  
−
== Пример программы ==
+
== Пример программ ==
−
Ниже приведен пример программы КИХ-фильтра, написанный на C :
+
* [[(Prog) Расчет FIR-фильтра по стандартной формуле (Си)‎|Расчет FIR-фильтра по стандартной формуле]]
−
<pre>
+
* [[(Prog) Расчет FIR-фильтра через ДПФ метод Overlap-Add (Си)‎|Расчет FIR-фильтра через ДПФ метод Overlap-Add]]
−
 
+
* [[(Prog) Расчет FIR-фильтра через ДПФ метод Overlap-Save‎|Расчет FIR-фильтра через ДПФ метод Overlap-Save‎]]
−
#define N 100 // порядок фильтра
+
* [[(Prog) Расчет FIR-фильтра через ДПФ над конечным полем‎‎|Расчет FIR-фильтра через ДПФ над конечным полем‎‎]]
−
float h[N] = { #include “f1.h” }; //вставка файла с известными коэффициентами фильтра
+
−
float x[N];
+
−
float y[N];
+
−
 
+
−
short my_FIR(short sample_data)
+
−
{
+
−
  float result = 0;
+
−
 
+
−
  for ( int i = N - 2 ; i >= 0 ; i-- )
+
−
  {
+
−
    x[i + 1] = x[i];
+
−
    y[i + 1] = y[i];
+
−
  }
+
−
 
+
−
  x[0] = (float)sample_data;
+
−
 
+
−
  for (int k = 0; k < N; k++)
+
−
  {
+
−
    result = result + x[k]*h[k];
+
−
  }
+
−
  y[0] = result;
+
−
 
+
−
  return ((short)result);
+
−
}
+
−
 
+
−
</pre>
+
  
 
== Построение КИХ-фильтров ==
 
== Построение КИХ-фильтров ==

Текущая версия на 14:27, 15 июля 2013

Фильтр с конечной импульсной характеристикой (Нерекурсивный фильтр, КИХ-фильтр) или FIR-фильтр (FIR сокр. от finite impulse response — конечная импульсная характеристика) — один из видов линейных цифровых фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какого-то момента времени она становится точно равной нулю). Такой фильтр называют ещё нерекурсивным из-за отсутствия обратной связи. Знаменатель передаточной функции такого фильтра — некая константа.

Динамические характеристики

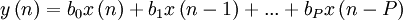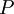Разностное уравнение, описывающее связь между входным и выходным сигналами фильтра: y\left (n\right)=b_0 x\left(n\right)+ b_1 x\left(n-1 \right)+...+b_P x\left(n-P \right) где P — порядок фильтра, 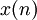x(n) — входной сигнал, 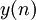y(n) — выходной сигнал, а 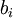b_{i} — коэффициенты фильтра. Иными словами, значение любого отсчета выходного сигнала определяется суммой масштабированных значений 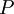P предыдущих отсчетов. Можно сказать иначе: значение выхода фильтра в любой момент времени есть значение отклика на мгновенное значение входа и сумма всех постепенно затухающих откликов 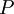P предыдущих отсчетов сигнала, которые всё ещё оказывают влияние на выход (после 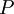P-отсчетов импульсная переходная функция становится равной нулю, как уже было сказано, поэтому все члены после 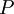P-го тоже станут равными нулю). Запишем предыдущее уравнение в более ёмком виде:

y \left( n \right) = \sum_{i=0}^{P} b_i x \left( n-i \right)

Для того, чтобы найти ядро фильтра положим

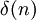x(n) = \delta(n)

где \delta(n) — дельта-функция. Тогда импульсная характеристика КИХ-фильтра может быть записана как:

h\left (n\right)=\sum_{i=0}^{P}b_i \delta\left(n-i\right)

Z-преобразование импульсной характеристики даёт нам передаточную функцию КИХ-фильтра:

H\left(z\right)=\sum_{i=0}^{P}b_i z^{-i}

Свойства

КИХ-фильтр обладает рядом полезных свойств, из-за которых он иногда более предпочтителен в использовании, чем БИХ-фильтр. Вот некоторые из них:

  • КИХ-фильтры устойчивы.
  • КИХ-фильтры при реализации не требуют наличия обратной связи.
  • Фаза КИХ-фильтров может быть сделана линейной

Прямая форма КИХ фильтра

КИХ фильтры могут быть реализованы с использованием трех элементов: умножитель, сумматор и блок задержки. Вариант, показанный на рисунке, есть прямая реализация КИХ-фильтров типа 1.

Реализация прямой формы КИХ фильтра

Пример программ

Построение КИХ-фильтров

Построение КИХ-фильтров заключается в выборе коэффициентов фильтра таким образом, чтобы полученная система имела требуемые характеристики. Чаще всего фильтр строят по заданной амплитудно-частотной характеристике. Существуют разные методы построения КИХ-фильтров:

  1. Построение методом окна
  2. Метод частотной выборки
  3. Метод наименьших квадратов
  4. Метод Паркса-Макклиллана (также известный как Equiripple, Optimal, или Minimax метод). Обычно используется алгоритм Ремеза, чтобы найти оптимальный набор equiripple-коэффициентов. Задаётся желаемая амплитудно-частотная характеристика, функция весов ошибки отклика и порядок фильтра N. Затем алгоритм находит множество из 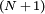\scriptstyle (N \,+\, 1) коэффициентов, которые минимизируют максимум отклонения от идеального отклика. Интуитивно понятно, что этот алгоритм находит фильтр, который имеет АЧХ близкую к желаемой с той точностью, которая может быть достигнута с использованием 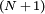\scriptstyle (N \,+\, 1) коэффициентов. Этот метод легко реализуется поскольку по крайней мере одна статья[1] включает в себя программу, которая принимает требуемую АЧХ и N, и возвращает оптимальные коэффициенты фильтра.
  5. Фильтры Чебышева могут быть с тем же успехом построены с использованием алгоритмов БПФ. Алгоритм итеративен по своей природе. Вычисляется ДПФ от начальной характеристики фильтра с помощью БПФ (в качестве начального приближения можно взять h[n]=delta[n]). В частотной области проводится коррекция АЧХ в соответствии со спецификациями и вычисляется ОДПФ. Во временной области оставляют только N коэффициентов(обнулив оставшиеся). Далее повторяют БПФ, коррекцию и т.д.

Программные пакеты такие как MATLAB, GNU Octave, Scilab, и SciPy реализуют описанные выше методы.

Некоторые спецификации на фильтр представляют собой форму входного сигнала во временной области, которую фильтр должен "распознавать". Оптимальный согласованный фильтр для выделения сигнала любой формы из белого шума получается путём дискретизации требуемой формы сигнала и использования полученных коэффициентов в обратном порядке в качестве коэффициентов фильтра — импульсная характеристика полученного фильтра является зеркальным отражением по времени требуемой формы входного сигнала.

Построение методом окна

В данном методе сначала строится идеальный БИХ-фильтр, затем к нему применяется Функция окна – во временной области, умножением бесконечной импульсной характеристики на функцию окна. Затем выполняется свёртка полученного результата с откликом на функцию окна. Если идеальная АЧХ достаточно проста, например, как прямоугольный отклик, результат свёртки можно сравнительно легко определить. На самом деле обычно сначала определяют требуемый результат и решают обратную задачу определения подходящей функции окна. Для этого метода особенно хорошо подходят окна Кайзера.

Пример КИХ-фильтра

Примером простого КИХ-фильтра может служить скользящее среднее, используемое для обработки сигналов и изображений, системах автоматического управления и для других прикладных целей. Разностное уравнение, которое характеризует фильтр скользящее среднее, является уравнением КИХ-фильтра. Пусть 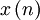x \left( n \right) — входной сигнал фильтра, 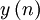y \left( n \right) — выходной сигнал. Тогда разностное уравнение будет иметь вид:

y \left( n \right) = \sum_{i=0}^{P} b_i x \left( n-i \right)

Отличительной особенностью скользящего среднего является равенство единице суммы коэффициентов 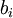\ b_i :

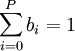\sum_{i=0}^{P} b_i = 1,

Последнее равенство отличает скользящее среднее от любого другого КИХ-фильтра. В частности для простого скользящего среднего:

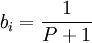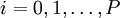
b_{i}=\frac{1}{P+1} для i=0,1,\dots,P

Для того, чтобы найти импульсную переходную функцию скользящего среднего делается следующее допущение:

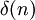\ x(n) = \delta(n)

где \ \delta(n) — дельта-функция. Тогда импульсная характеристика такого фильтра может быть записана как:

h\left (n\right)=\sum_{i=0}^{P}b_i \delta\left(n-i\right)

Z-преобразование импульсной характеристики даёт передаточную функцию:

H\left(z\right)=\sum_{i=0}^{P}b_i z^{-i}


Литература

  1. ↑ Rabiner, Lawrence R., and Gold, Bernard, 1975: Theory and Application of Digital Signal Processing (Englewood Cliffs, New Jersey: Prentice-Hall, Inc.) ISBN 0-13-914101-4

Ссылки

Источник — «https://vscripts.ru/w/index.php?title=Фильтр_с_конечной_импульсной_характеристикой&oldid=520»