Песочница — различия между версиями
Turbo (обсуждение | вклад) |
Turbo (обсуждение | вклад) |
||
| Строка 25: | Строка 25: | ||
# Количество операций требующихся для вычисления одного обратного БПФ длины 2<sup>N</sup> составляется (2<sup>N</sup>)*N операций комплексного умножения и (2<sup>N</sup>)*N операций комплексного сложения. При этом поскольку на обратном преобразовании мнимая часть у нас не нулевая, то комплексное умножение требует 4 целочисленных умножения и 2 целочисленных сложения. Однако если на входе были только целочисленные значения, то на выходе мнимая часть нас не интересует. Поэтому требуется только две операции целочисленного умножения и одна целочисленного сложения (''требуется уточнить''). | # Количество операций требующихся для вычисления одного обратного БПФ длины 2<sup>N</sup> составляется (2<sup>N</sup>)*N операций комплексного умножения и (2<sup>N</sup>)*N операций комплексного сложения. При этом поскольку на обратном преобразовании мнимая часть у нас не нулевая, то комплексное умножение требует 4 целочисленных умножения и 2 целочисленных сложения. Однако если на входе были только целочисленные значения, то на выходе мнимая часть нас не интересует. Поэтому требуется только две операции целочисленного умножения и одна целочисленного сложения (''требуется уточнить''). | ||
# Вычисления произведения сверток длины (M+L-1) требует (M+L-1) комплексных умножения что равноценно 4*(M+L-1) целочисленных умножения и 2*(M+L-1) целочисленных сложения. | # Вычисления произведения сверток длины (M+L-1) требует (M+L-1) комплексных умножения что равноценно 4*(M+L-1) целочисленных умножения и 2*(M+L-1) целочисленных сложения. | ||
| + | |||
| + | Что бы вычислить свертку через БПФ, требуется 2 прямых преобразования БПФ длины (M+L-1). Но в случае реализации аппаратного фильтра, его коэффициенты могут переведены в частотную область единоразово. Далее требуется (M+L-1) комплексных умножения, спектров сигналов. И далее одно обратное БПФ для восстановления результата, также длины (M+L-1). | ||
| + | |||
| + | Итого: Если (M+L-1)= 2<sup>N</sup>, то | ||
| + | * 2*(2<sup>N</sup>)*N + 4*(2<sup>N</sup>)*N + 2*(2<sup>N</sup>)*N = 8*(2<sup>N</sup>)*N - целочисленных умножения размерности B-бит. | ||
| + | * 2*(2<sup>N</sup>)*N + 2*(2<sup>N</sup>)*N + 2*(2<sup>N</sup>)*N = 6*(2<sup>N</sup>)*N - целочисленных сложения размерности 2*B-бит. | ||
| + | |||
| + | ==== Пример ==== | ||
| + | M = 1024 | ||
| + | L = 1024 | ||
| + | B = 8 бит | ||
| + | |||
| + | Выбираем ближайшую сверху к (M+L-1) степень двойки 2^11 = 2048 > (1024+1024-1). Итого потребуется: | ||
| + | * 8*2048*11 = 180224 - целочисленных умножения размерности 8-бит. | ||
| + | * 6*2048*11 = 135168 - целочисленных сложения размерности 16-бит. | ||
| + | |||
| + | === Свертка через БПФ в конечном поле === | ||
| + | |||
| + | Расчет количества операций через свертку БПФ в конечном поле сильно зависит от начальных данных. Так как на основе этих даннхы рассчитывается динамический диапазон и рассчитываются модулярные каналы. | ||
| + | |||
| + | Количество операций равно сумме: | ||
| + | 1) Операции на прямом преобразователе | ||
| + | 2) Операции на каждом из модулярных БПФ (всего N штук) | ||
| + | 3) Операции на каждом из модулярных умножений (всего N штук) | ||
| + | 4) Операции на каждом из обратных модулярных БПФ (всего N штук) | ||
| + | 5) Операции на обратном преобразователе в позиционную систему счисления | ||
| + | |||
| + | Рассмотрим на примере: | ||
| + | |||
| + | M = 128 | ||
| + | L = 128 | ||
| + | B = 10 бит | ||
| + | |||
| + | Для расчета системы подходит следующий набор модулей: {257 769 3329}, то есть N = 3. Максимальное значение на входе меньше чем 2<sub>B</sub> = 2<sub>10</sub> = 1024 | ||
| + | |||
| + | http://vscripts.ru/2012/prime-set-generator.php?bit=10&len=128&convtype=1 | ||
Версия 14:09, 22 июля 2013
Содержание
Количество операций необходимых для вычисления воздействия FIR-фильтра
Пусть задан FIR-фильтр длины M и большая последовательность данных длины K. В этом случае можно разбить последовательность на несколько отрезков длины L и выполнить свертку по методу Overlap-Add или Overlap-Save. При этом метод выполнения свертки оказывается не важен. И количество операций будет пропорционально (K/L)*OPER - где OPER - оличество операций для метода, которым мы делаем линейную свертку.
Количество операций необходимых для вычисления линейной свертки
Пусть задан фильтр длины M и последовательность L и битность входных данных B.
Свертка по обычной формуле
По опеределению свертка вычисляется по формуле: 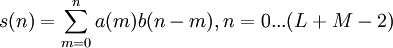
Для выполнения свертки в этом случае потребуется M*L операций умножения размерности B-бит и (M-1)*L операций сложения размерности 2*B-бит.
Пример
M = 1024 L = 1024 B = 8 бит
- Количество операций 16-битного сложения: 1047552
- Количество операций 8-битного умножения: 1048576
Свертка через БПФ по тригонометрическому базису
- Количество операций требующихся для вычисления одного прямого БПФ длины 2N составляет (2N)*N операций комплексного умножения и (2N)*N операций комплексного сложения. Каждая операция комплексного умножения/сложения на прямом БПФ требует две операции обычного умножения/сложения.
- Количество операций требующихся для вычисления одного обратного БПФ длины 2N составляется (2N)*N операций комплексного умножения и (2N)*N операций комплексного сложения. При этом поскольку на обратном преобразовании мнимая часть у нас не нулевая, то комплексное умножение требует 4 целочисленных умножения и 2 целочисленных сложения. Однако если на входе были только целочисленные значения, то на выходе мнимая часть нас не интересует. Поэтому требуется только две операции целочисленного умножения и одна целочисленного сложения (требуется уточнить).
- Вычисления произведения сверток длины (M+L-1) требует (M+L-1) комплексных умножения что равноценно 4*(M+L-1) целочисленных умножения и 2*(M+L-1) целочисленных сложения.
Что бы вычислить свертку через БПФ, требуется 2 прямых преобразования БПФ длины (M+L-1). Но в случае реализации аппаратного фильтра, его коэффициенты могут переведены в частотную область единоразово. Далее требуется (M+L-1) комплексных умножения, спектров сигналов. И далее одно обратное БПФ для восстановления результата, также длины (M+L-1).
Итого: Если (M+L-1)= 2N, то
- 2*(2N)*N + 4*(2N)*N + 2*(2N)*N = 8*(2N)*N - целочисленных умножения размерности B-бит.
- 2*(2N)*N + 2*(2N)*N + 2*(2N)*N = 6*(2N)*N - целочисленных сложения размерности 2*B-бит.
Пример
M = 1024 L = 1024 B = 8 бит
Выбираем ближайшую сверху к (M+L-1) степень двойки 2^11 = 2048 > (1024+1024-1). Итого потребуется:
- 8*2048*11 = 180224 - целочисленных умножения размерности 8-бит.
- 6*2048*11 = 135168 - целочисленных сложения размерности 16-бит.
Свертка через БПФ в конечном поле
Расчет количества операций через свертку БПФ в конечном поле сильно зависит от начальных данных. Так как на основе этих даннхы рассчитывается динамический диапазон и рассчитываются модулярные каналы.
Количество операций равно сумме: 1) Операции на прямом преобразователе 2) Операции на каждом из модулярных БПФ (всего N штук) 3) Операции на каждом из модулярных умножений (всего N штук) 4) Операции на каждом из обратных модулярных БПФ (всего N штук) 5) Операции на обратном преобразователе в позиционную систему счисления
Рассмотрим на примере:
M = 128 L = 128 B = 10 бит
Для расчета системы подходит следующий набор модулей: {257 769 3329}, то есть N = 3. Максимальное значение на входе меньше чем 2B = 210 = 1024
http://vscripts.ru/2012/prime-set-generator.php?bit=10&len=128&convtype=1