Нахождение обратного элемента по модулю — различия между версиями
Материал из Модулярная арифметики
Turbo (обсуждение | вклад) |
Turbo (обсуждение | вклад) |
||
| (не показано 5 промежуточных версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | Нахождение обратного элемента по модулю <math>|a^{-1}|_p</math>. То есть требуется найти x, такое что <math>|x*a|_p = 1</math>. Или если записать по другому: ax + py = 1. Для начала заметим, что элемент a кольца Zp обратим тогда и только тогда, когда НОД(a,p)=1. То есть ответ есть не всегда. Из определения обратного элемента прямо следует алгоритм. | + | Нахождение обратного элемента по модулю <math>|a^{-1}|_p</math>. То есть требуется найти <math>x</math>, такое что <math>|x*a|_p = 1</math>. Или если записать по другому: <math>ax + py = 1</math>. Для начала заметим, что элемент <math>a</math> кольца <math>Zp</math> обратим тогда и только тогда, когда НОД(a,p)=1. То есть ответ есть не всегда. Из определения обратного элемента прямо следует алгоритм. |
== Псевдокод == | == Псевдокод == | ||
| − | Входные данные: <math>a</math> из <math>Zp</math>. | + | *Входные данные: <math>a</math> из <math>Zp</math>. |
| − | Выходные данные: обратный к <math>a</math> в кольце, если он существует. | + | *Выходные данные: обратный к <math>a</math> в кольце, если он существует. |
| − | + | # Использовать расширенный алгоритм Евклида для нахождения x и y, таких что ax + ny = d. | |
| − | + | # Если d > 1, то обратного элемента не существует. Иначе возвращаем x. | |
== Код на Си == | == Код на Си == | ||
| Строка 43: | Строка 43: | ||
} | } | ||
</pre> | </pre> | ||
| + | |||
| + | == Программа он-лайн == | ||
| + | |||
| + | * [http://vscripts.ru/2013/find-inverse-by-mod.php Найти обратный элемент по модулю] | ||
Текущая версия на 05:52, 2 декабря 2013
Нахождение обратного элемента по модулю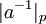 
. То есть требуется найти 
, такое что 
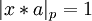. Или если записать по другому: 
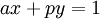. Для начала заметим, что элемент 
кольца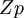 
обратим тогда и только тогда, когда НОД(a,p)=1. То есть ответ есть не всегда. Из определения обратного элемента прямо следует алгоритм.
Псевдокод
- Входные данные: из .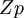
- Выходные данные: обратный к в кольце, если он существует.
- Использовать расширенный алгоритм Евклида для нахождения x и y, таких что ax + ny = d.
- Если d > 1, то обратного элемента не существует. Иначе возвращаем x.
Код на Си
#include <stdio.h>
/* calculates a * *x + b * *y = gcd(a, b) = *d */
void extended_euclid(long a, long b, long *x, long *y, long *d) {
long q, r, x1, x2, y1, y2;
if (b == 0) {
*d = a, *x = 1, *y = 0;
return;
}
x2 = 1, x1 = 0, y2 = 0, y1 = 1;
while (b > 0) {
q = a / b, r = a - q * b;
*x = x2 - q * x1, *y = y2 - q * y1;
a = b, b = r;
x2 = x1, x1 = *x, y2 = y1, y1 = *y;
}
*d = a, *x = x2, *y = y2;
}
/* computes the inverse of a modulo n */
long inverse(long a, long n) {
long d, x, y;
extended_euclid(a, n, &x, &y, &d);
if (d == 1) return x;
return 0;
}
int main(void) {
long a = 5, n = 7;
printf("Inverse of %ld modulo %2ld is %ld\n", a, n, inverse(a, n));
return 0;
}
