Описание работы универсального прямого преобразователя — различия между версиями
Turbo (обсуждение | вклад) (Новая страница: «== Описание работы универсального прямого преобразователя из позиционного представлени…») |
Turbo (обсуждение | вклад) |
||
| (не показано 6 промежуточных версии этого же участника) | |||
| Строка 3: | Строка 3: | ||
== Постановка задачи == | == Постановка задачи == | ||
| − | Требуется реализовать микроэлектронное устройство выполняющее преобразование из позиционного представления в модулярный код. Разработку будем вести на языке Verilog. Пусть задано входное число <math>X</math> в позиционном виде разрядности <math>N</math>-бит. Требуется найти остаток от его деления на каждое число из набора, образующих модулярный базис <math>{ | + | Требуется реализовать микроэлектронное устройство выполняющее преобразование из позиционного представления в модулярный код. Разработку будем вести на языке Verilog. Пусть задано входное число <math>X</math> в позиционном виде разрядности <math>N</math>-бит. Требуется найти остаток от его деления (вычет) на каждое число из набора, образующих модулярный базис <math>{p_1, p_2, ... p_m}</math>. Так как алгоритм вычисления остатков будет одинаков для каждого из них, то рассмотрим произвольное число из набора <math>p</math> размерности <math>k</math>-бит. |
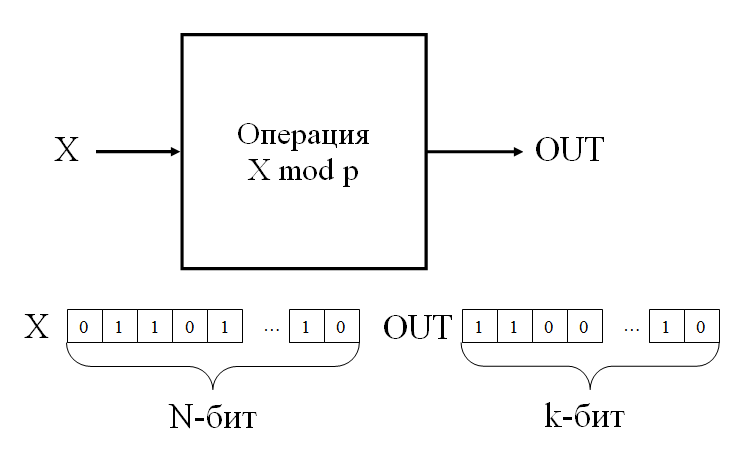
Схема этого блока с входами и выходами: | Схема этого блока с входами и выходами: | ||
| Строка 13: | Строка 13: | ||
* <math>0 \le OUT < p</math> | * <math>0 \le OUT < p</math> | ||
* <math>p</math> - константа заданная на этапе проектирования | * <math>p</math> - константа заданная на этапе проектирования | ||
| + | |||
| + | == Специальные случаи == | ||
| + | |||
| + | При некоторых соотношениях между входными данными и заданным p, модуль взятия остатка от деления можно реализовать простейшим образом. Рассмотрим такие случаи: | ||
| + | |||
| + | === Модуль больше входных данных === | ||
| + | |||
| + | <math>p > 2^N</math> - в этом случае выходные данные совпадают с входными, то есть <math>OUT = X</math>. | ||
| + | |||
| + | |||
| + | <source lang="verilog" line> | ||
| + | module forward_conv_module_23 (in, out); | ||
| + | input [3:0] in; // Max value: 15 | ||
| + | output [4:0] out; // Max value: 22 | ||
| + | assign out = {1'd0,in[3:0]}; | ||
| + | endmodule | ||
| + | </source> | ||
| + | |||
| + | === Модуль равен степени двойки === | ||
| + | |||
| + | <math>p = 2^t</math> - в этом случае выходные данные равны младшим t-бит входных данных, то есть <math>OUT = X[t:0]</math>. | ||
| + | |||
| + | |||
| + | <source lang="verilog" line> | ||
| + | module forward_conv_module_16 (out0, in); | ||
| + | output [3:0] out0; // Max value: 15 | ||
| + | input [7:0] in; // Max value: 255 | ||
| + | assign out0 = in[3:0]; | ||
| + | endmodule | ||
| + | </source> | ||
| + | |||
| + | === N незначительно превосходит разрядность модуля === | ||
| + | |||
| + | В этом случае достаточно проверить в какой из диапазонов вида <math>[0;p), [p;2 \cdot p), [2 \cdot p;3 \cdot p), ...</math> попадает <math>X</math> и вычесть из него поправочный коэффициент, соответствующий диапазону. <math>0</math> для <math>[0;p)</math>, <math>p</math> для <math>[p;2 \cdot p)</math>, <math>2 \cdot p</math> для <math>[2 \cdot p;3 \cdot p)</math> и.т.д. | ||
| + | |||
| + | |||
| + | <source lang="verilog" line> | ||
| + | module mod_253_511 (in, out); | ||
| + | input [8:0] in; | ||
| + | output reg [7:0] out; | ||
| + | always @ (in) | ||
| + | begin | ||
| + | if (in < 8'd253) | ||
| + | begin | ||
| + | out = in; | ||
| + | end | ||
| + | else if (in < 9'd506) | ||
| + | begin | ||
| + | out = in - 8'd253; | ||
| + | end | ||
| + | else | ||
| + | begin | ||
| + | out = in - 9'd506; | ||
| + | end | ||
| + | end | ||
| + | endmodule | ||
| + | |||
| + | module forward_conv_module_253 (in, out); | ||
| + | input [8:0] in; // Max value: 511 | ||
| + | output [7:0] out; // Max value: 252 | ||
| + | mod_253_511 inst(in, out); | ||
| + | endmodule | ||
| + | </source> | ||
| + | |||
| + | == Общий случай == | ||
| + | |||
| + | Представим входные данные <math>X</math> в следующем виде: | ||
| + | * <math>X = 2^0 \cdot X[0] + 2^1 \cdot X[1] + 2^2 \cdot X[2] + ... + 2^{N-1} \cdot X[N-1]</math> | ||
| + | и воспользуемся следующими свойствами вычетов: | ||
| + | * <math>|A + B|_p = ||A|_p + |B|_p|_p</math> и <math>|A \cdot B|_p = ||A|_p \cdot |B|_p|_p</math> | ||
| + | Тогда вычет X по модулю p можно записать следующим образом: | ||
| + | : <math>|X|_p = |2^0 \cdot X[0] + 2^1 \cdot X[1] + 2^2 \cdot X[2] + ... + 2^{N-1} \cdot X[N-1]|_p =</math> | ||
| + | : <math>= ||2^0|_p \cdot X[0] + |2^1|_p \cdot X[1] + |2^2|_p \cdot X[2] + ... + |2^{N-1}|_p \cdot X[N-1]|_p =</math> | ||
| + | : <math>= |A_0 \cdot X[0] + A_1 \cdot X[1] + A_2 \cdot X[2] + ... + A_{N-1} \cdot X[N-1]|_p</math>. | ||
| + | |||
| + | Константы вида <math>A_i = |2^i|_p</math> могут быть рассчитаны на этапе проектирования устройства и каждая константа не превосходит значение <math>p</math>. А общее значение выражения <math>SUM = (A_0 \cdot X[0] + ... + A_{N-1} \cdot X[N-1]) \le (p-1)*N</math>. Так как коэффициенты <math>A_i</math> известны, то оценку максимально возможного значения <math>SUM</math> можно сократить ещё больше. | ||
| + | |||
| + | Таким образом что бы посчитать значение вычета <math>|X|_p</math> требуется выполнить две операции: | ||
| + | 1) Найти сумму <math>SUM = (A_0 \cdot X[0] + ... + A_{N-1} \cdot X[N-1]) \le (p-1)*N</math>. | ||
| + | 2) Определить в какой интервал вида <math>[0;p), [p;2 \cdot p), [2 \cdot p;3 \cdot p), ... [(N-1) \cdot p;N \cdot p)</math> попадает значение <math>SUM</math> и вычесть из него соответствующее значение <math>0</math> для <math>[0;p)</math>, <math>p</math> для <math>[p;2 \cdot p)</math>, <math>2 \cdot p</math> для <math>[p;2 \cdot p)</math> и.т.д. | ||
| + | |||
| + | === Численный пример === | ||
| + | |||
| + | Пусть на входе у нас подается 10-битное число <math>X</math> и нам требуется найти его вычет (т.е. остаток от деления) на число 5. Запишем: | ||
| + | : <math>X = 2^0 \cdot X[0] + 2^1 \cdot X[1] + 2^2 \cdot X[2] + ... + 2^{9} \cdot X[9]</math> | ||
| + | : <math>X = X[0] + 2 \cdot X[1] + 4 \cdot X[2] + ... + 512 \cdot X[9]</math> | ||
| + | : <math>|X|_5 = |X[0] + |2|_5 \cdot X[1] + |4|_5 \cdot X[2] + ... + |512|_5 \cdot X[9]|_p</math> | ||
| + | Замечание: значение <math>X[i]</math> равно 0 или 1, т.е. меньше 5 поэтому <math>|X[i]|_p = X[i]</math> | ||
| + | : <math>|X|_5 = |SUM|_5 = |X[0] + 2 \cdot X[1] + 4 \cdot X[2] + 3 \cdot X[3] + 1 \cdot X[4] + 2 \cdot X[5] + 4 \cdot X[6] + 3 \cdot X[7] + 1 \cdot X[8] + 2 \cdot X[9]|_5</math>. | ||
| + | Что бы найти максимально возможное значение <math>SUM</math> достаточно сложить все коэффициенты <math>A_i</math>. | ||
| + | : <math>SUM_{MAX} = 1+2+4+3+1+2+4+3+1+2 = 23</math>. | ||
| + | |||
| + | То есть что бы найти значение <math>|X|_5</math>, надо проверить в какой из следующих интервалов попадает значение <math>SUM</math>. | ||
| + | : Если <math>0 <= SUM < 5</math>, то <math>|X|_5 = SUM</math> | ||
| + | : Если <math>5 <= SUM < 10</math>, то <math>|X|_5 = SUM - 5</math> | ||
| + | : Если <math>10 <= SUM < 15</math>, то <math>|X|_5 = SUM - 10</math> | ||
| + | : Если <math>15 <= SUM < 20</math>, то <math>|X|_5 = SUM - 15</math> | ||
| + | : Если <math>20 <= SUM < 25</math>, то <math>|X|_5 = SUM - 20</math> | ||
| + | |||
| + | === Verilog-код для численного примера === | ||
| + | |||
| + | <source lang="verilog" line> | ||
| + | module mod_5_23 (in, out); | ||
| + | input [4:0] in; | ||
| + | output reg [2:0] out; | ||
| + | always @ (in) | ||
| + | begin | ||
| + | if (in < 3'd5) | ||
| + | begin | ||
| + | out = in; | ||
| + | end | ||
| + | else if (in < 4'd10) | ||
| + | begin | ||
| + | out = in - 3'd5; | ||
| + | end | ||
| + | else if (in < 4'd15) | ||
| + | begin | ||
| + | out = in - 4'd10; | ||
| + | end | ||
| + | else if (in < 5'd20) | ||
| + | begin | ||
| + | out = in - 4'd15; | ||
| + | end | ||
| + | else | ||
| + | begin | ||
| + | out = in - 5'd20; | ||
| + | end | ||
| + | end | ||
| + | endmodule | ||
| + | |||
| + | module forward_conv_module_5 (in, out); | ||
| + | input [9:0] in; // Max value: 1023 | ||
| + | output [2:0] out; // Max value: 4 | ||
| + | wire [4:0] inter1; // Max value: 23 | ||
| + | assign inter1 = in[2:0] + 3*in[3] + in[4] + 2*in[5] + 4*in[6] + 3*in[7] + in[8] + 2*in[9]; | ||
| + | mod_5_23 inst(inter1, out); | ||
| + | endmodule | ||
| + | </source> | ||
| + | |||
| + | == Конвейеризация преобразователя == | ||
| + | |||
| + | * Так как в преобразователе есть два четко выраженных этапа, то в синхронных устройствах можно увеличить частоту работы преобразователя, за счет увеличения тактов вычисления с 1 до 2. На первом такте вычисляется сумма <math>SUM</math>, на втором ищется интервал, куда она попадает и затем корректируется с помощью вычитания. | ||
| + | * Если требуется дальнейшее увеличение тактовой частоты, то можно большой многовходовой сумматор из первого этапа сделать пирамидальным, с конвейеризацией каждой ступени пирамиды. | ||
| + | |||
| + | == Генератор Verilog == | ||
| + | |||
| + | * [http://vscripts.ru/2013/forward-converter-universal.php Генератор Verilog универсального прямого преобразователя для произвольных модулей] | ||
| + | |||
| + | == Результаты моделирования == | ||
| + | |||
| + | * [[Результаты синтеза универсальных прямых преобразователей для простых модулей в пределах 8 бит]] | ||
Текущая версия на 14:29, 18 декабря 2013
Содержание
Описание работы универсального прямого преобразователя из позиционного представления в модулярный код
Постановка задачи
Требуется реализовать микроэлектронное устройство выполняющее преобразование из позиционного представления в модулярный код. Разработку будем вести на языке Verilog. Пусть задано входное число 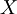 в позиционном виде разрядности
в позиционном виде разрядности 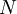 -бит. Требуется найти остаток от его деления (вычет) на каждое число из набора, образующих модулярный базис
-бит. Требуется найти остаток от его деления (вычет) на каждое число из набора, образующих модулярный базис 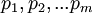 . Так как алгоритм вычисления остатков будет одинаков для каждого из них, то рассмотрим произвольное число из набора
. Так как алгоритм вычисления остатков будет одинаков для каждого из них, то рассмотрим произвольное число из набора  размерности
размерности 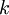 -бит.
-бит.
Схема этого блока с входами и выходами:
Здесь:
-
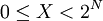
-
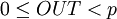
-
 - константа заданная на этапе проектирования
- константа заданная на этапе проектирования
Специальные случаи
При некоторых соотношениях между входными данными и заданным p, модуль взятия остатка от деления можно реализовать простейшим образом. Рассмотрим такие случаи:
Модуль больше входных данных
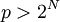 - в этом случае выходные данные совпадают с входными, то есть
- в этом случае выходные данные совпадают с входными, то есть 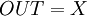 .
.
module forward_conv_module_23 (in, out);
input [3:0] in; // Max value: 15
output [4:0] out; // Max value: 22
assign out = {1'd0,in[3:0]};
endmodule
Модуль равен степени двойки
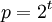 - в этом случае выходные данные равны младшим t-бит входных данных, то есть
- в этом случае выходные данные равны младшим t-бит входных данных, то есть ![OUT = X[t:0]](/w/images/math/8/e/8/8e8f19c11f52113a6c70c26019ae3c55.png) .
.
module forward_conv_module_16 (out0, in);
output [3:0] out0; // Max value: 15
input [7:0] in; // Max value: 255
assign out0 = in[3:0];
endmodule
N незначительно превосходит разрядность модуля
В этом случае достаточно проверить в какой из диапазонов вида 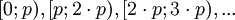 попадает
попадает 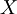 и вычесть из него поправочный коэффициент, соответствующий диапазону.
и вычесть из него поправочный коэффициент, соответствующий диапазону. 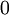 для
для 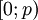 ,
,  для
для 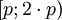 ,
, 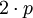 для
для 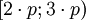 и.т.д.
и.т.д.
module mod_253_511 (in, out);
input [8:0] in;
output reg [7:0] out;
always @ (in)
beginif (in < 8'd253)
beginout = in;
endelse if (in < 9'd506)
beginout = in - 8'd253;
endelsebeginout = in - 9'd506;
endendendmodulemodule forward_conv_module_253 (in, out);
input [8:0] in; // Max value: 511
output [7:0] out; // Max value: 252
mod_253_511 inst(in, out);
endmodule
Общий случай
Представим входные данные 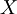 в следующем виде:
в следующем виде:
и воспользуемся следующими свойствами вычетов:
-
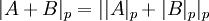 и
и 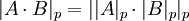
Тогда вычет X по модулю p можно записать следующим образом:
-
![|X|_p = |2^0 \cdot X[0] + 2^1 \cdot X[1] + 2^2 \cdot X[2] + ... + 2^{N-1} \cdot X[N-1]|_p =](/w/images/math/4/3/9/43969a893d9fac5b0f5ece384d430552.png)
-
![= ||2^0|_p \cdot X[0] + |2^1|_p \cdot X[1] + |2^2|_p \cdot X[2] + ... + |2^{N-1}|_p \cdot X[N-1]|_p =](/w/images/math/b/3/5/b3574f18ed42f0df6e555d264ff81097.png)
-
![= |A_0 \cdot X[0] + A_1 \cdot X[1] + A_2 \cdot X[2] + ... + A_{N-1} \cdot X[N-1]|_p](/w/images/math/f/d/f/fdfacb6ebe2a92d95c6b0f1c21668722.png) .
.
Константы вида 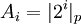 могут быть рассчитаны на этапе проектирования устройства и каждая константа не превосходит значение
могут быть рассчитаны на этапе проектирования устройства и каждая константа не превосходит значение  . А общее значение выражения
. А общее значение выражения ![SUM = (A_0 \cdot X[0] + ... + A_{N-1} \cdot X[N-1]) \le (p-1)*N](/w/images/math/3/3/4/334a7412d697fb2adcca647b5bd2eeef.png) . Так как коэффициенты
. Так как коэффициенты 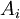 известны, то оценку максимально возможного значения
известны, то оценку максимально возможного значения 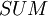 можно сократить ещё больше.
можно сократить ещё больше.
Таким образом что бы посчитать значение вычета 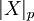 требуется выполнить две операции:
1) Найти сумму
требуется выполнить две операции:
1) Найти сумму ![SUM = (A_0 \cdot X[0] + ... + A_{N-1} \cdot X[N-1]) \le (p-1)*N](/w/images/math/3/3/4/334a7412d697fb2adcca647b5bd2eeef.png) .
2) Определить в какой интервал вида
.
2) Определить в какой интервал вида 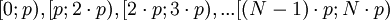 попадает значение
попадает значение 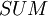 и вычесть из него соответствующее значение
и вычесть из него соответствующее значение 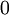 для
для 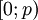 ,
,  для
для 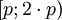 ,
, 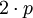 для
для 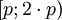 и.т.д.
и.т.д.
Численный пример
Пусть на входе у нас подается 10-битное число 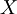 и нам требуется найти его вычет (т.е. остаток от деления) на число 5. Запишем:
и нам требуется найти его вычет (т.е. остаток от деления) на число 5. Запишем:
Замечание: значение ![X[i]](/w/images/math/6/5/7/65746d19c9d0244f2d991fc55895f871.png) равно 0 или 1, т.е. меньше 5 поэтому
равно 0 или 1, т.е. меньше 5 поэтому ![|X[i]|_p = X[i]](/w/images/math/4/9/c/49cfa35bb2ce3edaacd9200390112559.png)
-
![|X|_5 = |SUM|_5 = |X[0] + 2 \cdot X[1] + 4 \cdot X[2] + 3 \cdot X[3] + 1 \cdot X[4] + 2 \cdot X[5] + 4 \cdot X[6] + 3 \cdot X[7] + 1 \cdot X[8] + 2 \cdot X[9]|_5](/w/images/math/9/c/d/9cd8bb785faf6fa613d324851f49e529.png) .
.
Что бы найти максимально возможное значение 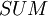 достаточно сложить все коэффициенты
достаточно сложить все коэффициенты 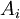 .
.
-
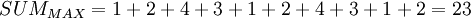 .
.
То есть что бы найти значение 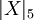 , надо проверить в какой из следующих интервалов попадает значение
, надо проверить в какой из следующих интервалов попадает значение 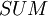 .
.
- Если
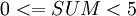 , то
, то 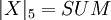
- Если
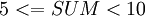 , то
, то 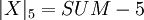
- Если
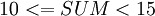 , то
, то 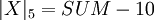
- Если
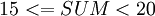 , то
, то 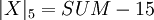
- Если
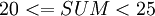 , то
, то 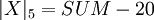
Verilog-код для численного примера
module mod_5_23 (in, out);
input [4:0] in;
output reg [2:0] out;
always @ (in)
beginif (in < 3'd5)
beginout = in;
endelse if (in < 4'd10)
beginout = in - 3'd5;
endelse if (in < 4'd15)
beginout = in - 4'd10;
endelse if (in < 5'd20)
beginout = in - 4'd15;
endelsebeginout = in - 5'd20;
endendendmodulemodule forward_conv_module_5 (in, out);
input [9:0] in; // Max value: 1023
output [2:0] out; // Max value: 4
wire [4:0] inter1; // Max value: 23
assign inter1 = in[2:0] + 3*in[3] + in[4] + 2*in[5] + 4*in[6] + 3*in[7] + in[8] + 2*in[9];
mod_5_23 inst(inter1, out);
endmodule
Конвейеризация преобразователя
- Так как в преобразователе есть два четко выраженных этапа, то в синхронных устройствах можно увеличить частоту работы преобразователя, за счет увеличения тактов вычисления с 1 до 2. На первом такте вычисляется сумма
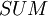 , на втором ищется интервал, куда она попадает и затем корректируется с помощью вычитания.
, на втором ищется интервал, куда она попадает и затем корректируется с помощью вычитания.
- Если требуется дальнейшее увеличение тактовой частоты, то можно большой многовходовой сумматор из первого этапа сделать пирамидальным, с конвейеризацией каждой ступени пирамиды.
![X = 2^0 \cdot X[0] + 2^1 \cdot X[1] + 2^2 \cdot X[2] + ... + 2^{N-1} \cdot X[N-1]](/w/images/math/0/7/f/07f0f2519203af1ab2271ad045f39fc7.png)
![X = 2^0 \cdot X[0] + 2^1 \cdot X[1] + 2^2 \cdot X[2] + ... + 2^{9} \cdot X[9]](/w/images/math/9/d/6/9d67a9bf3c6b7f153c4997e5c5dbd84b.png)
![X = X[0] + 2 \cdot X[1] + 4 \cdot X[2] + ... + 512 \cdot X[9]](/w/images/math/4/0/a/40ab6475329614ee88a3d0fe6beef6db.png)
![|X|_5 = |X[0] + |2|_5 \cdot X[1] + |4|_5 \cdot X[2] + ... + |512|_5 \cdot X[9]|_p](/w/images/math/c/a/c/cac4f1aae6b9be24bf499054b80acba7.png)