Метод умножения Шёнхаге — Штрассена — различия между версиями
Turbo (обсуждение | вклад) |
Turbo (обсуждение | вклад) |
||
| (не показаны 4 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''Алгоритм Шёнхаге - Штрассена''' - асимптотически быстрый алгоритм умножения больших чисел. Он был разработан Арнольдом Шёнхаге и Фолькером Штрассеном в 1971. Сложность алгоритма в нотации "О - большого" составляет O(''N'' log ''N'' log log ''N''). Алгоритм | |
| + | рекурсивно использует быстрое преобразование Фурье над кольцом из 2<sup>2<sup>''n''</sup></sup> + 1 элементов, специальный тип дискретного преобразования Фурье - теоретико-числовое преобразование. | ||
| + | |||
| + | Алгоритм Шёнхаге - Штрассена являлся наиболее быстрым асимптотически известным методом умножения с 1971 до 2007, когда Фюрером был предложен более быстрый метод. Тем не менее, алгоритм Фюрера в настоящее время имеет преимущество только для астрономически больших чисел и не используется на практике. | ||
| + | |||
| + | На практике алгоритм Шёнхаге - Штрассена начинает превосходить в скорости старые методы, такие как алгоритм Карацубы и алгоритм Тоома-Кука для чисел между 2<sup>2<sup>15</sup></sup> и 2<sup>2<sup>17</sup></sup> (от 10,000 до 40,000 десятичных разрядов). | ||
| + | |||
| + | Приложения алгоритма Шёнхаге - Штрассена включают в себя как чисто математические задачи, такие как поиск простых чисел Мерсенна и вычисление цифр числа ''π'', так и практические, такие как вычисление подстановки Кронекера, в которой умножение многочленов с целыми коэффициентами можно эффективно заменить умножением больших чисел; это используется на практике by GMP-ECM для факторизации целых чисел методом эллиптических кривых Ленстры. | ||
| + | |||
| + | == Теория == | ||
| + | |||
| + | |||
| + | |||
| + | === Свертка === | ||
| + | Допустим, что мы перемножаем числа 123 и 456 «в столбик», однако без выполнения переноса. Результат будет выглядеть так: | ||
| + | |||
| + | {|width=300 | ||
| + | | || || 1 || 2 || 3 | ||
| + | |- | ||
| + | | || ×|| 4 || 5 || 6 | ||
| + | |- | ||
| + | |colspan=5|<hr /> | ||
| + | |- | ||
| + | | || || 6 || 12 || 18 | ||
| + | |- | ||
| + | | || 5 || 10 || 15 || | ||
| + | |- | ||
| + | | 4 || 8 || 12 || || | ||
| + | |- | ||
| + | |colspan=5|<hr /> | ||
| + | |- | ||
| + | | 4 || 13 || 28 || 27 || 18 | ||
| + | |} | ||
| + | |||
| + | Эта последовательность (4, 13, 28, 27, 18) называется ''ациклической'' или ''линейной свёрткой'' от последовательностей (1,2,3) и (4,5,6). Зная ациклическую свёртку двух последовательностей, рассчитать произведение несложно: достаточно выполнить перенос (например, в самом правом столбце, мы оставляем 8 и добавляем 1 к столбцу, содержащему 27). В нашем примере это приводит к результату 56088. | ||
| + | |||
| + | Есть и другие типы свёрток, которые могут быть полезны. Допустим, что входящие последовательности содержат ''n'' элементов (в примере — 3). Тогда результирующая линейная свёртка содержит ''n'' + ''n'' − 1 элементов; если мы возьмём самый правый столбец ''n'' элементов и добавим самый левый столбец ''n'' − 1 ', в результате мы получим циклическую свёртку: | ||
| + | |||
| + | {|width=300 | ||
| + | | || 28 || 27 || 18 | ||
| + | |- | ||
| + | | + || || 4 || 13 | ||
| + | |- | ||
| + | |colspan=5|<hr /> | ||
| + | |- | ||
| + | | || 28 || 31 || 31 | ||
| + | |} | ||
| + | |||
| + | Если мы произведём перенос при циклическом свёртывании, результат будет тот же, что и при произведении чисел по модулю B<sup>''n''</sup> − 1 (в данном примере это 10<sup>3</sup> − 1 = 999). Выполним перенос по (28, 31, 31) и получим 3141, при этом 3141 ≡ 56088 (mod 999). | ||
| + | |||
| + | Наоборот, если мы возьмём самый правый столбец ''n'' элементов и ''вычтем'' самый левый столбец ''n''−1 элементов, то в результате мы получим обратную свёртку: | ||
| + | |||
| + | {|width=300 | ||
| + | | || 28 || 27 || 18 | ||
| + | |- | ||
| + | | − || || 4 || 13 | ||
| + | |- | ||
| + | |colspan=5|<hr /> | ||
| + | |- | ||
| + | | || 28 || 23 || 5 | ||
| + | |} | ||
| + | |||
| + | Если мы произведём перенос при обратном свёртывании, то результат будет тот же, что и при произведении чисел по модулю B<sup>''n''</sup> + 1. В данном примере, 10<sup>3</sup> + 1 = 1001, выполним перенос по (28, 23, 5) и получим 3035, при этом 3035 ≡ 56088 (mod 1001). Обратная свёртка может содержать отрицательные числа, которые могут быть убраны во время переноса, используя ту же технику, что и при длинных вычитаниях. | ||
| + | |||
| + | === Теорема о свёртке === | ||
| + | |||
| + | Как и другие методы, основанные на быстром преобразовании Фурье, алгоритм Шёнхаге - Штрассена в корне зависит от теоремы о свёртке, которая обеспечивает эффективный способ посчитать циклическую свёртку двух последовательностей. Её идея состоит в следующем: | ||
| + | |||
| + | : Циклическая свёртка двух векторов может быть найдена через [[дискретное преобразование Фурье]] (ДПФ) каждого из них, путём произведения результирующих векторов элемент за элементом, с последующим обратным преобразованием Фурье (ОДПФ). | ||
| + | |||
| + | Или через формулы: | ||
| + | |||
| + | : CyclicConvolution(X, Y) = IDFT(DFT(X) · DFT(Y)), где: | ||
| + | :: CyclicConvolution — ''циклическая свертка'', | ||
| + | :: DFT — ''дискретное преобразование Фурье'', | ||
| + | :: IDFT — ''обратное дискретное преобразование Фурье''. | ||
| + | |||
| + | Если мы посчитаем ДПФ и ОДПФ, используя быстрое преобразование Фурье, и вызовем наш алгоритм перемножения рекурсивно, чтобы перемножить входы(?) преобразованных векторов DFT(X) и DFT(Y), то в результате мы получим эффективный алгоритм для расчёта циклической свёртки. | ||
| + | |||
| + | В этом алгоритме, гораздо эффективней считать ''обратную циклическую'' свёртку; как оказывается, немного модифицированная версия теоремы о свёртке может позволить и это. Предположим, что вектора X и Y имеют длину ''n'', и ''a'' — примитивный корень порядка 2''n'' (это означает, что ''a''<sup>2''n''</sup> = 1 и все меньшие степени ''a'' не равны 1). Таким образом мы можем определить третий вектор ''A'', называемый ''вектор веса'', обладающий следующими свойствами: | ||
| + | [[Файл:DIT-FFT-butterfly.png|мини|Операция «[[бабочка (БПФ)|бабочка]]».]] | ||
| + | |||
| + | : ''A'' = (''a''<sup>''j''</sup>), 0 ≤ ''j'' < ''n'' | ||
| + | : ''A''<sup>−1</sup> = (''a''<sup>−j''</sup>), 0 ≤ ''j'' < ''n'' | ||
| + | |||
| + | Теперь мы можем записать: | ||
| + | |||
| + | : NegacyclicConvolution(''X'', ''Y'') = ''A''<sup>−1</sup> · IDFT(DFT(''A'' · ''X'') · DFT(''A'' · ''Y'')), где | ||
| + | :: NegacyclicConvolution — ''Обратная циклическая свертка'', | ||
| + | :: DFT — ''дискретное преобразование Фурье'', | ||
| + | :: IDFT — ''обратное дискретное преобразование Фурье''. | ||
| + | |||
| + | Другими словами, это то же самое за исключением того, что входящие векторы умножены на ''A'', а результат умножен на ''A''<sup>−1</sup>. | ||
| + | |||
| + | === Выбор кольца === | ||
| + | |||
| + | Дискретное преобразование Фурье — абстрактная операция, которая может быть выполнена в любом алгебраическом [[Кольцо (математика)|кольце]]; обычно оно берётся из поля комплексных чисел, но фактически использовать комплексную арифметику с достаточной точностью, чтобы обеспечить точные результаты, медленно и неэффективно. Вместо этого мы можем использовать теоретико-числовое преобразование, которое производит преобразование в поле целых чисел по модулю N для некоторого целого N. | ||
| + | |||
| + | Так же как есть примитивные корни единицы любого порядка на комплексной плоскости, при любом заданном ''n'' мы можем выбрать подходящее N такое, что ''b'' — примитивный корень единицы порядка ''n'' в поле целых чисел по модулю N (другими словами, ''b''<sup>''n''</sup> ≡ 1 (mod N), и все меньшие степени ''b'' не равны 1 mod N). | ||
| + | |||
| + | Алгоритм тратит большую часть времени на рекурсивное выполнение произведения меньших чисел; в простом варианте алгоритма это происходит в ряде мест: | ||
| + | |||
| + | # Внутри алгоритма быстрого преобразования Фурье, примитивный корень единицы ''b'' неоднократно возводится в степень и умножается на другие числа. | ||
| + | # При возведении в степень примитивного корня единицы ''a'' для получения вектора веса A с последующим умножением векторов A или A<sup>−1</sup> на другие вектора. | ||
| + | # При выполнении последовательного перемножения преобразованных векторов. | ||
| + | |||
| + | Ключевой момент — выбрать N, модуль, равный 2<sup>''n''</sup> + 1 для некоторого целого ''n''. У этого способа есть ряд преимуществ в ряде стандартных систем, в которых большие целые числа представлены в двоичном виде: | ||
| + | |||
| + | * Любое число может быть быстро уменьшено по модулю 2<sup>''n''</sup> + 1 используя только сдвиг и сложение. | ||
| + | * Любые примитивные корни единицы в этом кольце могут быть записаны в форме 2<sup>''k''</sup>; соответственно мы можем умножать или делить любое число на корень из единицы используя сдвиг. | ||
| + | * Поэлементное рекурсивное перемножение преобразованный векторов может быть выполнено, используя обратную свёртку, которая работает быстрее, чем ациклическая свёртка, и в которой уже есть уменьшение результата | ||
| + | по модулю 2<sup>''n''</sup> + 1. | ||
=== Пример === | === Пример === | ||
| − | Положим задано два числа: X и Y, каждое длиной | + | Следующий пример иллюстрирует работу алгоритма. |
| − | + | Положим задано два числа: X и Y, каждое длиной 8 бит. Требуется найти значение RES = (X*Y) mod 2<sup>N</sup>+1 | |
| − | + | Возьмём для определённости X = Y = 129<sub>10</sub> = 1000 0001<sub>2</sub>. | |
| − | * | + | Выберем N = 8 + 8 = 16. |
| − | ** N = | + | * Этап 1. Разбиение чисел на K = 4 слов длины M = 4 бита: |
| − | + | **Дополним числа нулями до длины N = 16 и разобьём на слова. Получим две последовательности (в данном примере идентичные): {0001, 1000, 0000, 0000}. Или в десятичном виде: {3, 8, 0, 0} (слова расположены в порядке от младших бит к старшим). Все операции далее выполняются по модулю 2<sup>n</sup>+1, где n выбирается из условия n >= 2*M + log2(K) и является степенью двойки, то есть в нашем случае n >= 2*4 + 2 = 10, n = 16. | |
| − | + | ||
| − | * Этап 2 | + | * Этап 2. Вычисление свёртки двух последовательностей: |
| − | + | ** Этап 2.1 Умножение последовательностей на весовые коэффициенты. 2K-ый корень из единицы в кольце из 2<sup>n</sup>+1 элементов равен 2<sup>2n/2K</sup> = 2<sup>4</sup> = 16. Результат умножения на вектор весовых коэффициентов в десятичном виде: {1, 128, 0, 0}. | |
| − | + | **Этап 2.2 Прямое преобразование Фурье над кольцом из 2<sup>n</sup> элементов. K-ый корень из единицы в кольце вычетов по модулю 2<sup>n</sup>+1 равен 2<sup>2n/2K</sup> = 2<sup>4</sup> = 256. Формула преобразования: <math>b_i = \sum^{K-1}_{j=0}{a_j\omega^{ij}}</math>, <math> \omega </math> - К-тый корень из единицы в кольце вычетов по модулю 2<sup>n</sup>+1. Результат: {129, 32769, 65410, 32770}. | |
| − | ** | + | **Этап 2.3 Покомпонентное произведение последовательностей в кольце из 2<sup>n</sup> элементов. Результат: {16641, 49153, 16129, 49155}. |
| − | + | **Этап 2.4 Обратное преобразование Фурье над кольцом из 2<sup>n</sup> элементов. Формула обратного преобразования: <math>b_i = \frac {1}{K} \sum^{K-1}_{j=0}{a_j\omega^{ij}}</math>, <math> \frac {1}{K} </math> - обратный к <math>K</math> по модулю 2<sup>n</sup>+1. Результат: {1, 256, 16384, 0}. | |
| − | ** n >= | + | **Этап 2.5 Умножение последовательностей на коэффициенты, обратные к используемым в 2.1. Результат: {1, 16, 64, 0}. |
| − | * Этап | + | * Этап 3. Выполнение операции переноса. Результат: {1, 0, 1, 4}. В двоичном виде: {0001, 0000, 0001, 0100} |
| − | + | * Этап 5. "Склейка" полученной последовательности, окончательный результат: 1010000001000<sub>2</sub> = 16641 = 129 * 129. | |
| − | ** | + | * Этап 5. Вычисление остатка по модулю 2<sup>N</sup>+1. В данном случае 16641 = 16641 mod 2<sup>16</sup>+1 |
| − | + | ||
| + | === Описание === | ||
| + | * [http://gmplib.org/manual/FFT-Multiplication.html#FFT-Multiplication Документация GMP LIB] | ||
| + | * [http://hal.archives-ouvertes.fr/docs/00/12/64/62/PDF/fft.pdf Статья A GMP-BASED IMPLEMENTATION OF SCHONHAGE-STRASSEN’S LARGE INTEGER MULTIPLICATION ALGORITHM] | ||
| + | * [http://en.wikipedia.org/wiki/Sch%C3%B6nhage%E2%80%93Strassen_algorithm Описание в английской Wikipedia] | ||
=== Исходники === | === Исходники === | ||
[http://www.ginac.de/CLN/cln.git/?p=cln.git;a=blob;f=src/base/digitseq/cl_DS_mul_fftm.h;h=a984802ce039e8179a26fda2681a2e133dba6fbd;hb=refs/heads/master CLN - Class Library for Numbers] | [http://www.ginac.de/CLN/cln.git/?p=cln.git;a=blob;f=src/base/digitseq/cl_DS_mul_fftm.h;h=a984802ce039e8179a26fda2681a2e133dba6fbd;hb=refs/heads/master CLN - Class Library for Numbers] | ||
| + | |||
| + | [https://github.com/myachik/ss_mult/blob/master/ss_mult.cpp Вариант реализации алгоритма] | ||
Текущая версия на 13:35, 21 апреля 2014
Алгоритм Шёнхаге - Штрассена - асимптотически быстрый алгоритм умножения больших чисел. Он был разработан Арнольдом Шёнхаге и Фолькером Штрассеном в 1971. Сложность алгоритма в нотации "О - большого" составляет O(N log N log log N). Алгоритм рекурсивно использует быстрое преобразование Фурье над кольцом из 22n + 1 элементов, специальный тип дискретного преобразования Фурье - теоретико-числовое преобразование.
Алгоритм Шёнхаге - Штрассена являлся наиболее быстрым асимптотически известным методом умножения с 1971 до 2007, когда Фюрером был предложен более быстрый метод. Тем не менее, алгоритм Фюрера в настоящее время имеет преимущество только для астрономически больших чисел и не используется на практике.
На практике алгоритм Шёнхаге - Штрассена начинает превосходить в скорости старые методы, такие как алгоритм Карацубы и алгоритм Тоома-Кука для чисел между 2215 и 2217 (от 10,000 до 40,000 десятичных разрядов).
Приложения алгоритма Шёнхаге - Штрассена включают в себя как чисто математические задачи, такие как поиск простых чисел Мерсенна и вычисление цифр числа π, так и практические, такие как вычисление подстановки Кронекера, в которой умножение многочленов с целыми коэффициентами можно эффективно заменить умножением больших чисел; это используется на практике by GMP-ECM для факторизации целых чисел методом эллиптических кривых Ленстры.
Содержание
Теория
Свертка
Допустим, что мы перемножаем числа 123 и 456 «в столбик», однако без выполнения переноса. Результат будет выглядеть так:
| 1 | 2 | 3 | ||
| × | 4 | 5 | 6 | |
| 6 | 12 | 18 | ||
| 5 | 10 | 15 | ||
| 4 | 8 | 12 | ||
| 4 | 13 | 28 | 27 | 18 |
Эта последовательность (4, 13, 28, 27, 18) называется ациклической или линейной свёрткой от последовательностей (1,2,3) и (4,5,6). Зная ациклическую свёртку двух последовательностей, рассчитать произведение несложно: достаточно выполнить перенос (например, в самом правом столбце, мы оставляем 8 и добавляем 1 к столбцу, содержащему 27). В нашем примере это приводит к результату 56088.
Есть и другие типы свёрток, которые могут быть полезны. Допустим, что входящие последовательности содержат n элементов (в примере — 3). Тогда результирующая линейная свёртка содержит n + n − 1 элементов; если мы возьмём самый правый столбец n элементов и добавим самый левый столбец n − 1 ', в результате мы получим циклическую свёртку:
| 28 | 27 | 18 | ||
| + | 4 | 13 | ||
| 28 | 31 | 31 | ||
Если мы произведём перенос при циклическом свёртывании, результат будет тот же, что и при произведении чисел по модулю Bn − 1 (в данном примере это 103 − 1 = 999). Выполним перенос по (28, 31, 31) и получим 3141, при этом 3141 ≡ 56088 (mod 999).
Наоборот, если мы возьмём самый правый столбец n элементов и вычтем самый левый столбец n−1 элементов, то в результате мы получим обратную свёртку:
| 28 | 27 | 18 | ||
| − | 4 | 13 | ||
| 28 | 23 | 5 | ||
Если мы произведём перенос при обратном свёртывании, то результат будет тот же, что и при произведении чисел по модулю Bn + 1. В данном примере, 103 + 1 = 1001, выполним перенос по (28, 23, 5) и получим 3035, при этом 3035 ≡ 56088 (mod 1001). Обратная свёртка может содержать отрицательные числа, которые могут быть убраны во время переноса, используя ту же технику, что и при длинных вычитаниях.
Теорема о свёртке
Как и другие методы, основанные на быстром преобразовании Фурье, алгоритм Шёнхаге - Штрассена в корне зависит от теоремы о свёртке, которая обеспечивает эффективный способ посчитать циклическую свёртку двух последовательностей. Её идея состоит в следующем:
- Циклическая свёртка двух векторов может быть найдена через дискретное преобразование Фурье (ДПФ) каждого из них, путём произведения результирующих векторов элемент за элементом, с последующим обратным преобразованием Фурье (ОДПФ).
Или через формулы:
- CyclicConvolution(X, Y) = IDFT(DFT(X) · DFT(Y)), где:
- CyclicConvolution — циклическая свертка,
- DFT — дискретное преобразование Фурье,
- IDFT — обратное дискретное преобразование Фурье.
Если мы посчитаем ДПФ и ОДПФ, используя быстрое преобразование Фурье, и вызовем наш алгоритм перемножения рекурсивно, чтобы перемножить входы(?) преобразованных векторов DFT(X) и DFT(Y), то в результате мы получим эффективный алгоритм для расчёта циклической свёртки.
В этом алгоритме, гораздо эффективней считать обратную циклическую свёртку; как оказывается, немного модифицированная версия теоремы о свёртке может позволить и это. Предположим, что вектора X и Y имеют длину n, и a — примитивный корень порядка 2n (это означает, что a2n = 1 и все меньшие степени a не равны 1). Таким образом мы можем определить третий вектор A, называемый вектор веса, обладающий следующими свойствами:
- A = (aj), 0 ≤ j < n
- A−1 = (a−j), 0 ≤ j < n
Теперь мы можем записать:
- NegacyclicConvolution(X, Y) = A−1 · IDFT(DFT(A · X) · DFT(A · Y)), где
- NegacyclicConvolution — Обратная циклическая свертка,
- DFT — дискретное преобразование Фурье,
- IDFT — обратное дискретное преобразование Фурье.
Другими словами, это то же самое за исключением того, что входящие векторы умножены на A, а результат умножен на A−1.
Выбор кольца
Дискретное преобразование Фурье — абстрактная операция, которая может быть выполнена в любом алгебраическом кольце; обычно оно берётся из поля комплексных чисел, но фактически использовать комплексную арифметику с достаточной точностью, чтобы обеспечить точные результаты, медленно и неэффективно. Вместо этого мы можем использовать теоретико-числовое преобразование, которое производит преобразование в поле целых чисел по модулю N для некоторого целого N.
Так же как есть примитивные корни единицы любого порядка на комплексной плоскости, при любом заданном n мы можем выбрать подходящее N такое, что b — примитивный корень единицы порядка n в поле целых чисел по модулю N (другими словами, bn ≡ 1 (mod N), и все меньшие степени b не равны 1 mod N).
Алгоритм тратит большую часть времени на рекурсивное выполнение произведения меньших чисел; в простом варианте алгоритма это происходит в ряде мест:
- Внутри алгоритма быстрого преобразования Фурье, примитивный корень единицы b неоднократно возводится в степень и умножается на другие числа.
- При возведении в степень примитивного корня единицы a для получения вектора веса A с последующим умножением векторов A или A−1 на другие вектора.
- При выполнении последовательного перемножения преобразованных векторов.
Ключевой момент — выбрать N, модуль, равный 2n + 1 для некоторого целого n. У этого способа есть ряд преимуществ в ряде стандартных систем, в которых большие целые числа представлены в двоичном виде:
- Любое число может быть быстро уменьшено по модулю 2n + 1 используя только сдвиг и сложение.
- Любые примитивные корни единицы в этом кольце могут быть записаны в форме 2k; соответственно мы можем умножать или делить любое число на корень из единицы используя сдвиг.
- Поэлементное рекурсивное перемножение преобразованный векторов может быть выполнено, используя обратную свёртку, которая работает быстрее, чем ациклическая свёртка, и в которой уже есть уменьшение результата
по модулю 2n + 1.
Пример
Следующий пример иллюстрирует работу алгоритма. Положим задано два числа: X и Y, каждое длиной 8 бит. Требуется найти значение RES = (X*Y) mod 2N+1 Возьмём для определённости X = Y = 12910 = 1000 00012. Выберем N = 8 + 8 = 16.
- Этап 1. Разбиение чисел на K = 4 слов длины M = 4 бита:
- Дополним числа нулями до длины N = 16 и разобьём на слова. Получим две последовательности (в данном примере идентичные): {0001, 1000, 0000, 0000}. Или в десятичном виде: {3, 8, 0, 0} (слова расположены в порядке от младших бит к старшим). Все операции далее выполняются по модулю 2n+1, где n выбирается из условия n >= 2*M + log2(K) и является степенью двойки, то есть в нашем случае n >= 2*4 + 2 = 10, n = 16.
- Этап 2. Вычисление свёртки двух последовательностей:
- Этап 2.1 Умножение последовательностей на весовые коэффициенты. 2K-ый корень из единицы в кольце из 2n+1 элементов равен 22n/2K = 24 = 16. Результат умножения на вектор весовых коэффициентов в десятичном виде: {1, 128, 0, 0}.
- Этап 2.2 Прямое преобразование Фурье над кольцом из 2n элементов. K-ый корень из единицы в кольце вычетов по модулю 2n+1 равен 22n/2K = 24 = 256. Формула преобразования:
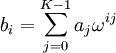 ,
, 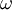 - К-тый корень из единицы в кольце вычетов по модулю 2n+1. Результат: {129, 32769, 65410, 32770}.
- К-тый корень из единицы в кольце вычетов по модулю 2n+1. Результат: {129, 32769, 65410, 32770}.
- Этап 2.3 Покомпонентное произведение последовательностей в кольце из 2n элементов. Результат: {16641, 49153, 16129, 49155}.
- Этап 2.4 Обратное преобразование Фурье над кольцом из 2n элементов. Формула обратного преобразования:
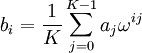 ,
, 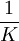 - обратный к
- обратный к 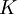 по модулю 2n+1. Результат: {1, 256, 16384, 0}.
по модулю 2n+1. Результат: {1, 256, 16384, 0}.
- Этап 2.5 Умножение последовательностей на коэффициенты, обратные к используемым в 2.1. Результат: {1, 16, 64, 0}.
- Этап 3. Выполнение операции переноса. Результат: {1, 0, 1, 4}. В двоичном виде: {0001, 0000, 0001, 0100}
- Этап 5. "Склейка" полученной последовательности, окончательный результат: 10100000010002 = 16641 = 129 * 129.
- Этап 5. Вычисление остатка по модулю 2N+1. В данном случае 16641 = 16641 mod 216+1
Описание
- Документация GMP LIB
- Статья A GMP-BASED IMPLEMENTATION OF SCHONHAGE-STRASSEN’S LARGE INTEGER MULTIPLICATION ALGORITHM
- Описание в английской Wikipedia