Рекурсивная модулярная арифметика — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| + | = Принцип рекурсивных модулярных вычислений = | ||
| + | |||
Рекурсивная модулярная арифметика основана на принципе глубокого распараллеливания модульных операций модулярной арифметики с основаниями <math>p_1,p_2,\ldots,p_n</math> посредством сведения модульных операций по каждому рабочему основанию <math>p_j</math>, <math>i<=j<=n</math> к модульным вычислениям по предшествующим рабочим основаниям <math>p_1,p_2,\ldots,p_{i-1}</math>, имеющим то или иное технологическое преимущество (например, малобитным), которые называются базисными основаниями. Такая редукция допустима только при выполнении так называемого условия согласования вычислительных диапазонов по каждому рабочему модулю <math>p_j</math> с вычислительными диапазонами по соответствующим комплексам базисных оснований. | Рекурсивная модулярная арифметика основана на принципе глубокого распараллеливания модульных операций модулярной арифметики с основаниями <math>p_1,p_2,\ldots,p_n</math> посредством сведения модульных операций по каждому рабочему основанию <math>p_j</math>, <math>i<=j<=n</math> к модульным вычислениям по предшествующим рабочим основаниям <math>p_1,p_2,\ldots,p_{i-1}</math>, имеющим то или иное технологическое преимущество (например, малобитным), которые называются базисными основаниями. Такая редукция допустима только при выполнении так называемого условия согласования вычислительных диапазонов по каждому рабочему модулю <math>p_j</math> с вычислительными диапазонами по соответствующим комплексам базисных оснований. | ||
Принцип согласования гарантирует, во-первых, изоморфизм кольцевых операций по соответствующим им комплексам базисных оснований, и во-вторых, выполнимость обращения каждого шага рекурсии посредством перевода соответствующих модулярных кодов по базисным основаниям в позиционный код (например, на основе китайской теоремы об остатках, или переводом их в полиадический код). | Принцип согласования гарантирует, во-первых, изоморфизм кольцевых операций по соответствующим им комплексам базисных оснований, и во-вторых, выполнимость обращения каждого шага рекурсии посредством перевода соответствующих модулярных кодов по базисным основаниям в позиционный код (например, на основе китайской теоремы об остатках, или переводом их в полиадический код). | ||
Несмотря на ограничения, которые накладываются на систему модулей, предложенный метод обеспечивает выигрыш по скорости и может быть применен в параллельных высокоскоростных вычислительных устройствах. | Несмотря на ограничения, которые накладываются на систему модулей, предложенный метод обеспечивает выигрыш по скорости и может быть применен в параллельных высокоскоростных вычислительных устройствах. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Пример == | == Пример == | ||
| Строка 20: | Строка 17: | ||
4) Столь малая разрядность базовых модулей позволяет эффективно реализовать модульные операции по базисным модулям в комбинационных схемах. | 4) Столь малая разрядность базовых модулей позволяет эффективно реализовать модульные операции по базисным модулям в комбинационных схемах. | ||
| + | Однако имеется ряд ограничений, которые должны быть выполнены и которые приводят к усложнению устройств, созданных по данной методике. Рассмотрим эти ограничения. | ||
| + | |||
| + | Пусть есть система базисных модулей <math>p_1,p_2,\ldots,p_m</math> и необходимо представить вычеты по модулю <math>p_{m+1}</math> через вычеты по этой системе базовых модулей. Очевидно, что максимальный вычет по модулю <math>p_{m+1}</math> равен <math>max=p_{m+1}-1</math>. Зная это значение и последовательность выполняемых операций, можно рассчитать максимальное значение <math>MAX</math> результата арифметической операции. Очевидно, что для однозначного представления результата арифметических операций необходимо, чтобы <math>MAX<Q</math>, где <math>Q=p_1\cdot p_2\cdot \ldots \cdot p_m</math>. Для остальных модулей расчет производится аналогично. | ||
= Представление данных и основные операции рекурсивной модулярной арифметики = | = Представление данных и основные операции рекурсивной модулярной арифметики = | ||
Версия 14:06, 23 апреля 2014
Содержание
Принцип рекурсивных модулярных вычислений
Рекурсивная модулярная арифметика основана на принципе глубокого распараллеливания модульных операций модулярной арифметики с основаниями 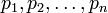 посредством сведения модульных операций по каждому рабочему основанию
посредством сведения модульных операций по каждому рабочему основанию 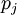 ,
, 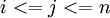 к модульным вычислениям по предшествующим рабочим основаниям
к модульным вычислениям по предшествующим рабочим основаниям 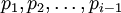 , имеющим то или иное технологическое преимущество (например, малобитным), которые называются базисными основаниями. Такая редукция допустима только при выполнении так называемого условия согласования вычислительных диапазонов по каждому рабочему модулю
, имеющим то или иное технологическое преимущество (например, малобитным), которые называются базисными основаниями. Такая редукция допустима только при выполнении так называемого условия согласования вычислительных диапазонов по каждому рабочему модулю 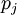 с вычислительными диапазонами по соответствующим комплексам базисных оснований.
Принцип согласования гарантирует, во-первых, изоморфизм кольцевых операций по соответствующим им комплексам базисных оснований, и во-вторых, выполнимость обращения каждого шага рекурсии посредством перевода соответствующих модулярных кодов по базисным основаниям в позиционный код (например, на основе китайской теоремы об остатках, или переводом их в полиадический код).
Несмотря на ограничения, которые накладываются на систему модулей, предложенный метод обеспечивает выигрыш по скорости и может быть применен в параллельных высокоскоростных вычислительных устройствах.
с вычислительными диапазонами по соответствующим комплексам базисных оснований.
Принцип согласования гарантирует, во-первых, изоморфизм кольцевых операций по соответствующим им комплексам базисных оснований, и во-вторых, выполнимость обращения каждого шага рекурсии посредством перевода соответствующих модулярных кодов по базисным основаниям в позиционный код (например, на основе китайской теоремы об остатках, или переводом их в полиадический код).
Несмотря на ограничения, которые накладываются на систему модулей, предложенный метод обеспечивает выигрыш по скорости и может быть применен в параллельных высокоскоростных вычислительных устройствах.
Пример
Поясним процедуру рекурсивных преобразований на простом примере. Возьмем в качестве базисных модулей двухбитные простые числа 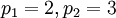 . Очевидно, что вычетами по модулям 2 и 3 можно однозначно представить любой вычет по модулю 5. В то же время вычетами по модулям 2, 3 и 5, где вычеты по модулю 5 представимы по модулям 2 и 3, можно однозначно представить любой вычет по модулю 29. Вычетами по модулям 2, 3, 5 и 29 можно однозначно представить любой вычет по модулю 863. И так далее пока не получим нужный набор рабочих оснований: 2, 3, 5, 29, 863,… Данный пример наглядно иллюстрирует 4 факта:
. Очевидно, что вычетами по модулям 2 и 3 можно однозначно представить любой вычет по модулю 5. В то же время вычетами по модулям 2, 3 и 5, где вычеты по модулю 5 представимы по модулям 2 и 3, можно однозначно представить любой вычет по модулю 29. Вычетами по модулям 2, 3, 5 и 29 можно однозначно представить любой вычет по модулю 863. И так далее пока не получим нужный набор рабочих оснований: 2, 3, 5, 29, 863,… Данный пример наглядно иллюстрирует 4 факта:
1) Аппаратные и временные затраты на представление чисел по базовым модулям 2 и 3 примерно одинаковы (оба базисных модуля двухбитные);
2) Наблюдается более высокая степень распараллеливаемости;
3) Появляется регулярность (все вычисления проводятся по модулям 2 и 3);
4) Столь малая разрядность базовых модулей позволяет эффективно реализовать модульные операции по базисным модулям в комбинационных схемах.
Однако имеется ряд ограничений, которые должны быть выполнены и которые приводят к усложнению устройств, созданных по данной методике. Рассмотрим эти ограничения.
Пусть есть система базисных модулей 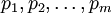 и необходимо представить вычеты по модулю
и необходимо представить вычеты по модулю 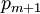 через вычеты по этой системе базовых модулей. Очевидно, что максимальный вычет по модулю
через вычеты по этой системе базовых модулей. Очевидно, что максимальный вычет по модулю 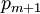 равен
равен 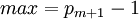 . Зная это значение и последовательность выполняемых операций, можно рассчитать максимальное значение
. Зная это значение и последовательность выполняемых операций, можно рассчитать максимальное значение 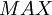 результата арифметической операции. Очевидно, что для однозначного представления результата арифметических операций необходимо, чтобы
результата арифметической операции. Очевидно, что для однозначного представления результата арифметических операций необходимо, чтобы 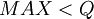 , где
, где 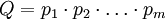 . Для остальных модулей расчет производится аналогично.
. Для остальных модулей расчет производится аналогично.