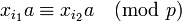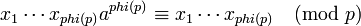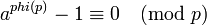Вычисление мультипликативных обратных элементов по заданному модулю — различия между версиями
Isaeva (обсуждение | вклад) (Новая страница: «Рассмотрим вопрос о мультипликативных обратных элементов по заданному модулю в фактор-…») |
Isaeva (обсуждение | вклад) |
||
| Строка 2: | Строка 2: | ||
Рассмотрим два способа вычисления обратных мультипликативных элементов. Первый способ основан на рассмотренном выше алгоритме Евклида, второй – на теореме Эйлера. | Рассмотрим два способа вычисления обратных мультипликативных элементов. Первый способ основан на рассмотренном выше алгоритме Евклида, второй – на теореме Эйлера. | ||
| + | |||
| + | |||
| + | '''Определение''' | ||
| + | |||
| + | Функция Эйлера <math>phi (n)</math> — это количество чисел от <math>1</math> до <math>n</math>, взаимно простых с <math>n</math>. | ||
| + | |||
| + | |||
| + | Т.е. это количество таких натуральных чисел из отрезка [1; n], наибольший общий делитель (НОД) которых с <math>n</math> равен единице. | ||
| + | |||
| + | |||
| + | '''Tеоремa Эйлера''' | ||
| + | |||
| + | Если <math>a</math> и <math>p</math> взаимно просты, то <math>a^{phi(p)} \equiv 1 \pmod p</math>, где <math>phi (n)</math> - функция Эйлера. | ||
| + | |||
| + | |||
| + | Доказательство. | ||
| + | |||
| + | Пусть <math>x_1, \dots, x_{\varphi(p)}</math> — все различные натуральные числа, меньшие <math>p</math> и взаимно простые с ним. | ||
| + | |||
| + | Рассмотрим все возможные произведения <math>x_i a</math> для всех <math>i</math> от <math>1</math> до <math>\varphi(p)</math>. | ||
| + | |||
| + | Поскольку <math>a</math> взаимно просто с <math>p</math> и <math>x_i</math> взаимно просто с <math>p</math>, то и <math>x_i a</math> также взаимно просто с <math>p</math>, то есть <math>x_i a \equiv x_j\pmod p</math> для некоторого <math>j</math>. | ||
| + | |||
| + | Отметим, что все остатки <math>x_i a</math> при делении на <math>p</math> различны. Действительно, пусть это не так, то существуют такие <math>i_1 \neq i_2</math>, что | ||
| + | : <math>x_{i_1} a \equiv x_{i_2} a\pmod p</math> | ||
| + | или | ||
| + | : <math>(x_{i_1} - x_{i_2}) a \equiv 0\pmod p</math>. | ||
| + | |||
| + | Так как <math>a</math> взаимно просто с <math>p</math>, то последнее равенство равносильно тому, что | ||
| + | : <math>x_{i_1} - x_{i_2} \equiv 0\pmod p</math> или <math>x_{i_1} \equiv x_{i_2}\pmod p</math>. | ||
| + | Это противоречит тому, что числа <math>x_1, \dots, x_{phi(p)}</math> попарно различны по модулю <math>p</math>. | ||
| + | |||
| + | Перемножим все сравнения вида <math>x_i a \equiv x_j\pmod p</math>. Получим: | ||
| + | : <math>x_1 \cdots x_{phi(p)} a^{phi(p)} \equiv x_1 \cdots x_{phi(p)}\pmod p</math> | ||
| + | или | ||
| + | : <math>x_1 \cdots x_{phi(p)} (a^{phi(p)}-1) \equiv 0\pmod p</math>. | ||
| + | Так как число <math>x_1 \cdots x_{phi(p)}</math> взаимно просто с <math>p</math>, то последнее сравнение равносильно тому, что | ||
| + | : <math>a^{phi(p)}-1 \equiv 0\pmod p</math> | ||
| + | или | ||
| + | :<math>a^{phi(p)} \equiv 1\pmod p</math>. | ||
| + | |||
| + | |||
| + | В частном случае, когда <math>p</math> простое, теорема Эйлера превращается в так называемую малую теорему Ферма: | ||
| + | |||
| + | '''Малая теорема Ферма''' | ||
| + | |||
| + | Если <math>p</math> - простое число и <math>a</math> - произвольное целое число, не делящееся на <math>p</math>, то <math>a^{p-1} \equiv 1 \pmod p </math>. | ||
Версия 17:15, 4 сентября 2014
Рассмотрим вопрос о мультипликативных обратных элементов по заданному модулю в фактор-кольце 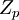 .
.
Рассмотрим два способа вычисления обратных мультипликативных элементов. Первый способ основан на рассмотренном выше алгоритме Евклида, второй – на теореме Эйлера.
Определение
Функция Эйлера 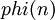 — это количество чисел от
— это количество чисел от 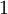 до
до 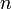 , взаимно простых с
, взаимно простых с 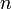 .
.
Т.е. это количество таких натуральных чисел из отрезка [1; n], наибольший общий делитель (НОД) которых с 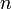 равен единице.
равен единице.
Tеоремa Эйлера
Если  и
и  взаимно просты, то
взаимно просты, то 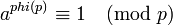 , где
, где 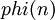 - функция Эйлера.
- функция Эйлера.
Доказательство.
Пусть 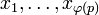 — все различные натуральные числа, меньшие
— все различные натуральные числа, меньшие  и взаимно простые с ним.
и взаимно простые с ним.
Рассмотрим все возможные произведения 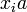 для всех
для всех 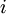 от
от 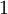 до
до 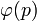 .
.
Поскольку  взаимно просто с
взаимно просто с  и
и 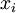 взаимно просто с
взаимно просто с  , то и
, то и 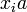 также взаимно просто с
также взаимно просто с  , то есть
, то есть 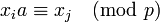 для некоторого
для некоторого 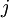 .
.
Отметим, что все остатки 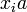 при делении на
при делении на  различны. Действительно, пусть это не так, то существуют такие
различны. Действительно, пусть это не так, то существуют такие 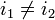 , что
, что
или
-
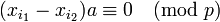 .
.
Так как  взаимно просто с
взаимно просто с  , то последнее равенство равносильно тому, что
, то последнее равенство равносильно тому, что
-
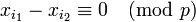 или
или 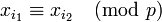 .
.
Это противоречит тому, что числа 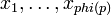 попарно различны по модулю
попарно различны по модулю  .
.
Перемножим все сравнения вида 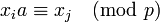 . Получим:
. Получим:
или
-
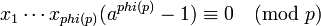 .
.
Так как число  взаимно просто с
взаимно просто с  , то последнее сравнение равносильно тому, что
, то последнее сравнение равносильно тому, что
или
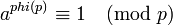 .
.
В частном случае, когда  простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
Малая теорема Ферма
Если  - простое число и
- простое число и  - произвольное целое число, не делящееся на
- произвольное целое число, не делящееся на  , то
, то 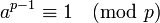 .
.