Описание КТО II — различия между версиями
DimaT (обсуждение | вклад) (Новая страница: «== Китайская теорема об остатках "второй версии"== При детальном рассмотрении, то что в [1] …») |
DimaT (обсуждение | вклад) (→Китайская теорема об остатках "второй версии") |
||
| (не показано 12 промежуточных версии этого же участника) | |||
| Строка 2: | Строка 2: | ||
При детальном рассмотрении, то что в [1] называется CRT II, по сути является ни чем иным, как обратным преобразователем на основе преобразования в полиадический код, в несколько видоизмененном виде. За основу взята стратегия devide and conquer (такая же стратегия используется в БПФ). | При детальном рассмотрении, то что в [1] называется CRT II, по сути является ни чем иным, как обратным преобразователем на основе преобразования в полиадический код, в несколько видоизмененном виде. За основу взята стратегия devide and conquer (такая же стратегия используется в БПФ). | ||
| − | Базисом КТО II является формула восстановления числа по двум остаткам <math>x_1, x_2</math>, по основаниям <math> | + | Базисом КТО II является формула восстановления числа по двум остаткам <math>x_1, x_2</math>, по основаниям <math>p_1, p_2</math>: |
| − | + | ||
| + | <math>X=x_1+||x_2-x_1|_{p_2}\cdot|p_1^{-1}|_{p_2}|_{p_2} \cdot p_1</math> | ||
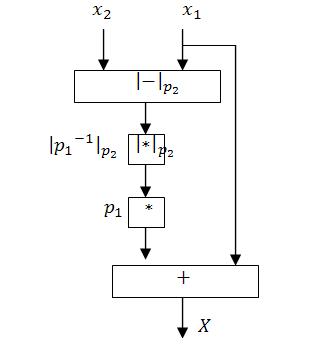
| + | Как мы можем видеть, формула является переводом на базе перевода в полиадический код. Архитектура такого преобразователя можно изобразить следующим образом: | ||
| + | [[Файл:Crt2 1.JPG]] | ||
| + | Если мы рассмотрим модулярную систему с большим числом оснований, то принцип состоит в следующем: | ||
| + | * Разбиваем имеющиеся вычеты по парам | ||
| + | * По базовой формуле для всех пар находим <math>X_1, X_2, ...</math>. Это будут вычеты по произведениям пар модулей | ||
| + | * Возвращаемся на пункт 1 с новыми вычетами <math>X_1, X_2, ...</math> и новыми модулями <math>P_k=p_{i} \cdot p_j</math> | ||
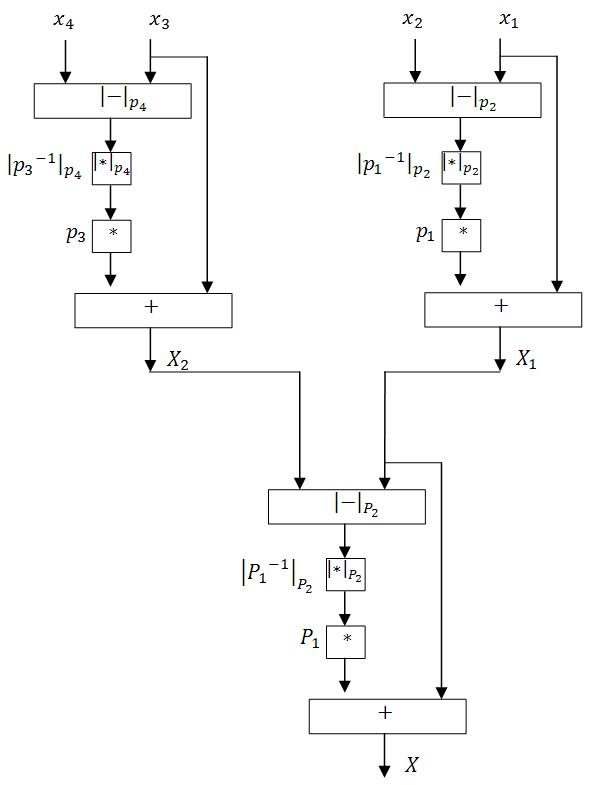
| + | В качестве '''примера''' рассмотрим реализацию обратного преобразователя для четырех оснований <math>p_1, p_2, p_3, p_4</math> и четырех остатков <math>x_1, x_2, x_3, x_4</math>: | ||
| + | * ''1 этап. Находим остаток <math>X_1</math> числа <math>X</math> по модулю <math>P_1=p_1*p_2</math>'' | ||
| + | <math>|X|_{p_1*p_2}=X_1=x_1+||x_2-x_1|_{p_2} \cdot |p_1^{-1}|_{p_2}|_{p_2} \cdot p_1</math> | ||
| + | |||
| + | * ''2 этап. Находим остаток <math>X_2</math> числа <math>X</math> по модулю <math>P_2=p_3*p_4</math>'' | ||
| + | <math>|X|_{p_3*p_4}=X_2=x_3+||x_4-x_3|_{p_4} \cdot |p_3^{-1}|_{p_4}|_{p_4} \cdot p_3</math> | ||
| + | |||
| + | |||
| + | * ''3 этап. Находим <math>X</math> по остаткам <math>X_1</math> и <math>X_2</math> и модулям <math>P_1</math> и <math>P_2</math>'' | ||
| + | <math>X=X_1+||X_2-X_1|_{P_2}\cdot|P_1^{-1}|_{P_2}|_{P_2} \cdot P_1</math> | ||
| + | |||
| + | [[Файл:Crt2 2.JPG]] | ||
| + | |||
| + | |||
| + | Преимущества данной структуры над обычным преобразователем через смешанную систему оснований еще требует проверки. | ||
[1]Yuke Wang, “Residue-to-Binary Converters Based On New Chinese Remainder Theorems,” IEEE Transactions on Circuits and Systems – II: Analog and Digital Signal Processing, vol. 47, No. 3, pp.197–205, March 2000. | [1]Yuke Wang, “Residue-to-Binary Converters Based On New Chinese Remainder Theorems,” IEEE Transactions on Circuits and Systems – II: Analog and Digital Signal Processing, vol. 47, No. 3, pp.197–205, March 2000. | ||
Текущая версия на 07:00, 8 апреля 2013
Китайская теорема об остатках "второй версии"
При детальном рассмотрении, то что в [1] называется CRT II, по сути является ни чем иным, как обратным преобразователем на основе преобразования в полиадический код, в несколько видоизмененном виде. За основу взята стратегия devide and conquer (такая же стратегия используется в БПФ).
Базисом КТО II является формула восстановления числа по двум остаткам 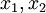 , по основаниям
, по основаниям 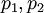 :
:
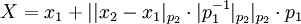
Как мы можем видеть, формула является переводом на базе перевода в полиадический код. Архитектура такого преобразователя можно изобразить следующим образом:
Если мы рассмотрим модулярную систему с большим числом оснований, то принцип состоит в следующем:
- Разбиваем имеющиеся вычеты по парам
- По базовой формуле для всех пар находим
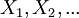 . Это будут вычеты по произведениям пар модулей
. Это будут вычеты по произведениям пар модулей
- Возвращаемся на пункт 1 с новыми вычетами
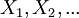 и новыми модулями
и новыми модулями 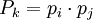
В качестве примера рассмотрим реализацию обратного преобразователя для четырех оснований 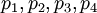 и четырех остатков
и четырех остатков 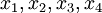 :
:
- 1 этап. Находим остаток
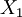 числа
числа 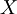 по модулю
по модулю 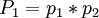
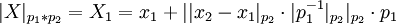
- 2 этап. Находим остаток
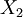 числа
числа 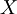 по модулю
по модулю 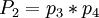
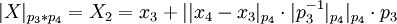
- 3 этап. Находим
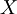 по остаткам
по остаткам 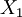 и
и 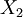 и модулям
и модулям 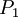 и
и 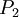
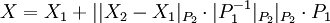
Преимущества данной структуры над обычным преобразователем через смешанную систему оснований еще требует проверки.
[1]Yuke Wang, “Residue-to-Binary Converters Based On New Chinese Remainder Theorems,” IEEE Transactions on Circuits and Systems – II: Analog and Digital Signal Processing, vol. 47, No. 3, pp.197–205, March 2000.