Свёртка (цифровая обработка сигналов) — различия между версиями
Turbo (обсуждение | вклад) |
Turbo (обсуждение | вклад) |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 6: | Строка 6: | ||
Линейной сверткой сигналов <math>a(n)</math> и <math>b(n)</math> называется дискретный сигнал вида: | Линейной сверткой сигналов <math>a(n)</math> и <math>b(n)</math> называется дискретный сигнал вида: | ||
| − | <math>s(n)=\sum_{m=0}^{n}a(m)b(n-m), n=0...N+M-2</math> | + | <math>s(n)=\sum_{m=0}^{n}a(m)b(n-m), n=0...(N+M-2)</math> |
| − | Для вычисления линейной свертки сигналы a(n)и b(n)сдвигают относительно друг друга почленно перемножают и складывают. При этом предполагается, что a(n)=0 при n<0 и | + | Для вычисления линейной свертки сигналы <math>a(n)</math> и <math>b(n)</math> сдвигают относительно друг друга почленно перемножают и складывают. При этом предполагается, что <math>a(n)=0</math> при <math>n<0</math> и <math>n\ge N</math>, и <math>b(n)=0</math> при <math>n<0</math> и <math>n\ge M</math>. |
== Циклическая свёртка == | == Циклическая свёртка == | ||
| − | В циклической свертке предполагается, что дискретные сигналы <math>a(n)</math> и <math>b(n)</math> – периодические с одинаковым периодом N отсчетов. Тогда циклической сверткой сигналов a(n) и b(n) называется сигнал вида: | + | В циклической свертке предполагается, что дискретные сигналы <math>a(n)</math> и <math>b(n)</math> – периодические с одинаковым периодом <math>N</math> отсчетов. Тогда циклической сверткой сигналов <math>a(n)</math> и <math>b(n)</math> называется сигнал вида: |
| − | s(n)= | + | <math>s(n)=\sum_{m=0}^{n}a(m)b(n-m), n=0...N-1 </math> |
| − | Результат циклической свертки также имеет длину N отсчетов. | + | Результат циклической свертки также имеет длину <math>N</math> отсчетов. |
== Вычисление линейной свертки через циклическую == | == Вычисление линейной свертки через циклическую == | ||
| − | Используя циклическую свертку можно рассчитать линейную свертку двух сигналов. Для этого необходимо каждый из сигналов a(n)и b(n) длительностью M и N отсчетов соответственно дополнить нулями до длины M+N-1. Вычисление линейной свертки через циклическую кажется нерациональным, однако на практике чаще бывает удобно вычислять именно циклическую свертку, благодаря так называемой [http://mathworld.wolfram.com/ConvolutionTheorem.html теореме о свертке]. Cуть теоремы о свертке: спектр циклической свертки есть произведение спектров сворачиваемых сигналов: S(k)=A(k)*B(k), где A(k) и B(k) - спектры сворачиваемых сигналов, S(k) - спектр циклической свертки двух сигналов. Где спектр есть ни что иное как [http://ru.wikipedia.org/wiki/%D0%94%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%A4%D1%83%D1%80%D1%8C%D0%B5 Дискретное преобразование Фурье (ДПФ)], для реализации которого можно использовать [http://ru.wikipedia.org/wiki/%D0%91%D1%8B%D1%81%D1%82%D1%80%D0%BE%D0%B5_%D0%BF%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%A4%D1%83%D1%80%D1%8C%D0%B5 быстрые алгоритмы БПФ] | + | Используя циклическую свертку можно рассчитать линейную свертку двух сигналов. Для этого необходимо каждый из сигналов <math>a(n)</math> и <math>b(n)</math> длительностью <math>M</math> и <math>N</math> отсчетов соответственно дополнить нулями до длины <math>M+N-1</math>. Вычисление линейной свертки через циклическую кажется нерациональным, однако на практике чаще бывает удобно вычислять именно циклическую свертку, благодаря так называемой [http://mathworld.wolfram.com/ConvolutionTheorem.html теореме о свертке]. Cуть теоремы о свертке: спектр циклической свертки есть произведение спектров сворачиваемых сигналов: <math>S(k)=A(k)*B(k)</math>, где <math>A(k)</math> и <math>B(k)</math> - спектры сворачиваемых сигналов, <math>S(k)</math> - спектр циклической свертки двух сигналов. Где спектр есть ни что иное как [http://ru.wikipedia.org/wiki/%D0%94%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%A4%D1%83%D1%80%D1%8C%D0%B5 Дискретное преобразование Фурье (ДПФ)], для реализации которого можно использовать [http://ru.wikipedia.org/wiki/%D0%91%D1%8B%D1%81%D1%82%D1%80%D0%BE%D0%B5_%D0%BF%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%A4%D1%83%D1%80%D1%8C%D0%B5 быстрые алгоритмы БПФ]. |
== Применение == | == Применение == | ||
* Линейная свертка используется для расчета FIR-фильтров в цифровой обработке сигналов. | * Линейная свертка используется для расчета FIR-фильтров в цифровой обработке сигналов. | ||
* Циклическую свертку используют для вычисления линейной свертки в том случае, если теорема о свертке дает хороший результат. | * Циклическую свертку используют для вычисления линейной свертки в том случае, если теорема о свертке дает хороший результат. | ||
Текущая версия на 09:33, 29 июля 2013
Свёртка (англ. Convolution) — это базовая операция в задачах цифровой обработки сигналов. В дискретном случае различают два вида сверток: линейную и циклическую.
Пусть имеется два дискретных сигнала 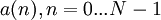 и
и 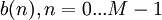 . В общем случае
. В общем случае 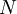 и
и 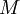 отличаются.
отличаются.
Содержание
Линейная свёртка
Линейной сверткой сигналов 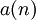 и
и 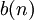 называется дискретный сигнал вида:
называется дискретный сигнал вида:
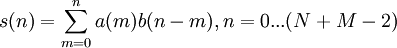
Для вычисления линейной свертки сигналы 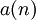 и
и 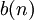 сдвигают относительно друг друга почленно перемножают и складывают. При этом предполагается, что
сдвигают относительно друг друга почленно перемножают и складывают. При этом предполагается, что  при
при 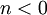 и
и 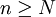 , и
, и 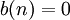 при
при 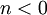 и
и 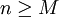 .
.
Циклическая свёртка
В циклической свертке предполагается, что дискретные сигналы 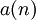 и
и 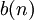 – периодические с одинаковым периодом
– периодические с одинаковым периодом 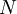 отсчетов. Тогда циклической сверткой сигналов
отсчетов. Тогда циклической сверткой сигналов 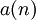 и
и 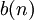 называется сигнал вида:
называется сигнал вида:
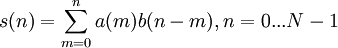 Результат циклической свертки также имеет длину
Результат циклической свертки также имеет длину 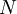 отсчетов.
отсчетов.
Вычисление линейной свертки через циклическую
Используя циклическую свертку можно рассчитать линейную свертку двух сигналов. Для этого необходимо каждый из сигналов 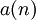 и
и 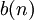 длительностью
длительностью 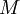 и
и 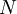 отсчетов соответственно дополнить нулями до длины
отсчетов соответственно дополнить нулями до длины 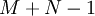 . Вычисление линейной свертки через циклическую кажется нерациональным, однако на практике чаще бывает удобно вычислять именно циклическую свертку, благодаря так называемой теореме о свертке. Cуть теоремы о свертке: спектр циклической свертки есть произведение спектров сворачиваемых сигналов:
. Вычисление линейной свертки через циклическую кажется нерациональным, однако на практике чаще бывает удобно вычислять именно циклическую свертку, благодаря так называемой теореме о свертке. Cуть теоремы о свертке: спектр циклической свертки есть произведение спектров сворачиваемых сигналов: 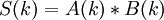 , где
, где 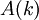 и
и 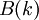 - спектры сворачиваемых сигналов,
- спектры сворачиваемых сигналов, 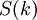 - спектр циклической свертки двух сигналов. Где спектр есть ни что иное как Дискретное преобразование Фурье (ДПФ), для реализации которого можно использовать быстрые алгоритмы БПФ.
- спектр циклической свертки двух сигналов. Где спектр есть ни что иное как Дискретное преобразование Фурье (ДПФ), для реализации которого можно использовать быстрые алгоритмы БПФ.
Применение
- Линейная свертка используется для расчета FIR-фильтров в цифровой обработке сигналов.
- Циклическую свертку используют для вычисления линейной свертки в том случае, если теорема о свертке дает хороший результат.