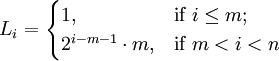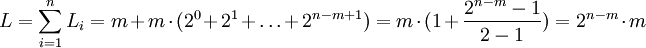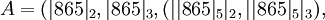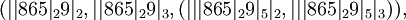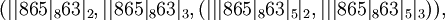Рекурсивная модулярная арифметика — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| (не показано 10 промежуточных версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
= Принцип рекурсивных модулярных вычислений = | = Принцип рекурсивных модулярных вычислений = | ||
| − | Рекурсивная модулярная арифметика основана на принципе глубокого распараллеливания модульных операций модулярной арифметики с основаниями <math>p_1,p_2,\ldots,p_n</math> посредством сведения модульных операций по каждому рабочему основанию <math>p_j</math>, <math>i | + | Система модулей традиционной модулярной арифметики может быть выражена через систему субмодулей меньшей размерности с использованием рекурсии. |
| + | |||
| + | Рекурсивная модулярная арифметика основана на принципе глубокого распараллеливания модульных операций модулярной арифметики с основаниями <math>p_1,p_2,\ldots,p_n</math> посредством сведения модульных операций по каждому рабочему основанию <math>p_j</math>, <math>i\le j\le n</math> к модульным вычислениям по предшествующим рабочим основаниям <math>p_1,p_2,\ldots,p_{i-1}</math>, имеющим то или иное технологическое преимущество (например, малобитным), которые называются базисными основаниями. Такая редукция допустима только при выполнении так называемого условия согласования вычислительных диапазонов по каждому рабочему модулю <math>p_j</math> с вычислительными диапазонами по соответствующим комплексам базисных оснований. | ||
| + | |||
Принцип согласования гарантирует, во-первых, изоморфизм кольцевых операций по соответствующим им комплексам базисных оснований, и во-вторых, выполнимость обращения каждого шага рекурсии посредством перевода соответствующих модулярных кодов по базисным основаниям в позиционный код (например, на основе китайской теоремы об остатках, или переводом их в полиадический код). | Принцип согласования гарантирует, во-первых, изоморфизм кольцевых операций по соответствующим им комплексам базисных оснований, и во-вторых, выполнимость обращения каждого шага рекурсии посредством перевода соответствующих модулярных кодов по базисным основаниям в позиционный код (например, на основе китайской теоремы об остатках, или переводом их в полиадический код). | ||
| + | |||
| + | Рекурсивное представление данных позволяет устранить некоторые недостатки модулярной арифметики. В частности, нивелируется неоднородность модульных вычислителей по сложности и времени выполнения операций. | ||
Несмотря на ограничения, которые накладываются на систему модулей, предложенный метод обеспечивает выигрыш по скорости и может быть применен в параллельных высокоскоростных вычислительных устройствах. | Несмотря на ограничения, которые накладываются на систему модулей, предложенный метод обеспечивает выигрыш по скорости и может быть применен в параллельных высокоскоростных вычислительных устройствах. | ||
| Строка 26: | Строка 31: | ||
Возьмем в качестве базисных модулей все взаимно простые трехбитные числа: 4, 5 и 7. В этом случае <math>Q=4\cdot 5\cdot 7=140</math>. | Возьмем в качестве базисных модулей все взаимно простые трехбитные числа: 4, 5 и 7. В этом случае <math>Q=4\cdot 5\cdot 7=140</math>. | ||
| + | |||
| + | Таким образом, выбираем <math> p_i = 11 </math> (ближайшее к 7 простое число). Далее совокупность рабочих модулей строится с помощью аналогичного расчета, пока не будет достигнут требуемый вычислительный диапазон. | ||
| + | |||
| + | Наконец, рассмотрим реальный случай. Пусть нам нужно реализовать преобразователь Фурье для 24-битных аргументов при количестве точек 1024. | ||
| + | Для этого потребуется вычислять сумму 1024 произведений, т.е. обеспечить <math> 1024 \cdot max^2 < Q </math>. Здесь уже не обойтись системой только трехбитных базисных модулей. Добавим к ним четырехбитные: 5, 7, 8, 9, 11 и 13 (Q = 360360). | ||
| + | Для выбора ближайшего рабочего модуля необходимо <math> \sqrt \frac{Q}{1024}</math>. | ||
| + | |||
| + | Получаем <math>p_{i}-1 < 32 </math>. | ||
| + | Выбираем <math>p_{i} = 31 </math>. | ||
| + | |||
| + | Аналогичным расчетом реализуем рекурсивное дерево рабочих оснований целиком. | ||
| + | |||
| + | Чтобы сделать такое устройство, нужно спроектировать блок из 6 вычислителей (для каждого базисного модуля), потребуется 16 таких блоков. Вот где работает регулярность. | ||
| + | |||
| + | Заметим, что все вычислители будут иметь высокую скорость модульных операций (суперраспараллеливание) и небольшие аппаратные затраты в силу малости базисных модулей или их близости к степеням двойки. | ||
| + | |||
| + | |||
| + | Таким образом, предложенный аппарат рекурсивных модулярных вычислений дает следующие преимущества: | ||
| + | : 1. Устранение дисбаланса в операциях с малыми и большими модулями (аппаратные и временные затраты примерно одинаковы, т.к. в идеале все базисные модули имеют одинаковое число бит). | ||
| + | : 2. Существенно более высокая степень распараллеливаемости, а значит и более высокое быстродействие. | ||
| + | : 3. Появляется регулярность (большое количество одинаковых базисных модулей). | ||
| + | : 4. Малая разрядность базисных модулей позволяет реализовать модульные операции на комбинационных схемах, оптимизированных в базисе булевых функций. | ||
= Представление данных и основные операции рекурсивной модулярной арифметики = | = Представление данных и основные операции рекурсивной модулярной арифметики = | ||
| + | |||
| + | Идея, на которой базируется рекурсивная модулярная арифметика: выразить систему модулей через систему субмодулей, имеющую меньшую размерность. | ||
| + | |||
| + | Пусть задана система модулей <math> p_1, p_2, \ldots, p_i, \ldots , p_n </math> и задан некоторый вектор <math> A = (a_1, a_2, \ldots , a_n) </math>. Выразим <math> a_i </math> через систему субмодулей | ||
| + | |||
| + | :<math> p_i = (p_{i,1}, p_{i,2}, \ldots , p_{i,k}) </math> , где <math> P_i = p_{i,1}, p_{i,2}, \ldots , p_{i,k} </math> и <math> a_i < P_i </math>: <math> a_i = (a_{i,1}, a_{i,2}, \ldots , a_{i,k}) </math>. | ||
| + | |||
| + | В этом случае вектор A можно представить в следующем виде: | ||
| + | |||
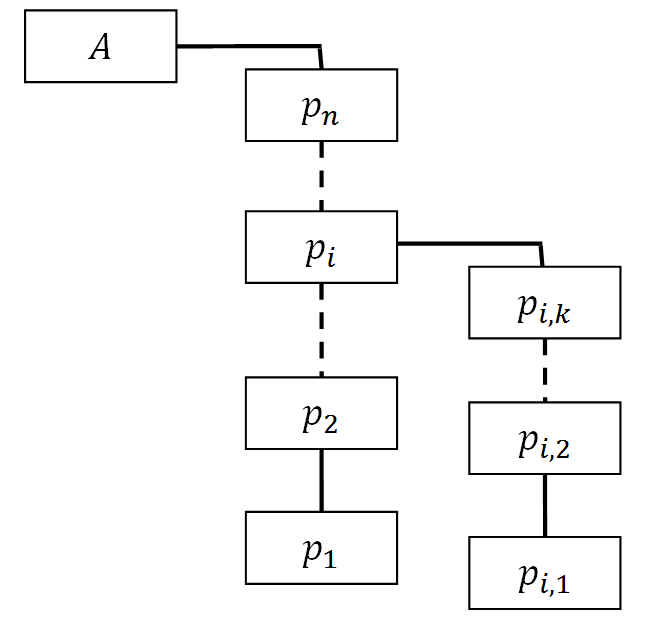
| + | :<math> (a_1, a_2, \ldots , a_{i-1}, (a_{i,1}, a_{i,2}, \ldots , a_{i,k}), a_{i+1}, \ldots , a_n) </math>, см. рисунок 1. | ||
| + | |||
| + | |||
| + | [[изображение:RecModArith_01.png|frame|center|Рис.1. Иерархия в модулярной арифметике]] | ||
| + | |||
| + | |||
| + | Назовем систему из m младших модулей системой базовых модулей, а их произведение обозначим <math> Q = (p_1 \cdot p_2 \cdot \ldots \cdot p_m) </math>. | ||
| + | |||
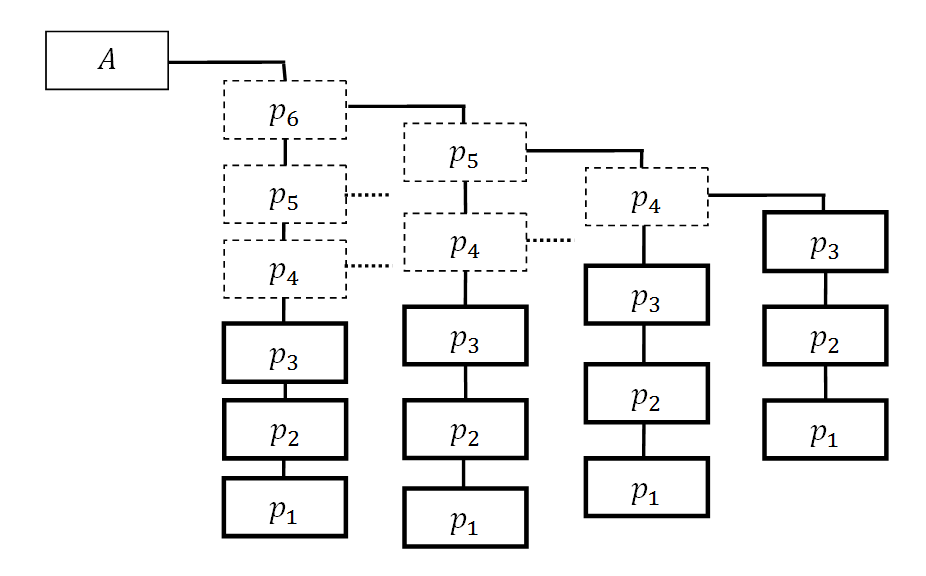
| + | Пусть <math> P_{i,1} = p_i, p_{i,2} = p_2, \ldots , p_{i,i-1} = p_{i-1} </math> , а <math> k = i-1 </math>, тогда при <math> i = m+1, \ldots , n </math> имеет место рекурсия. <math> a_i = (a_1, a_2, \ldots , a_m, a_{m+1}, \ldots , a_{i-1}) </math> по системе модулей <math> p_1, p_2, \ldots , p_m, p_{m+1}, \ldots , p_{i-1} </math> или, раскрывая рекурсию: <math> a_i = (a_1, a_2, \ldots , a_m, (a_{m+1,1}, a_{m+1,2}, \ldots , a_{m+1,m} ), \ldots) </math>. На рис.2 приведен частный случай разложения элемента <math> a_i </math> для случая <math> n=6 </math> и <math> m=3 </math>. | ||
| + | |||
| + | |||
| + | [[изображение:RecModArith_02.png|frame|center|Рис.2. Рекурсивное разложение элемента p6 через систему субмодулей (p1,p2,p3)]] | ||
| + | |||
== Прямое преобразование числа из позиционной системы счисления в представление рекурсивной модулярной арифметики == | == Прямое преобразование числа из позиционной системы счисления в представление рекурсивной модулярной арифметики == | ||
| + | |||
| + | Если в традиционной модулярной арифметике число элементов вектора равно числу элементов в системе модулей, то в рекурсивной модулярной арифметике количество элементов вектора увеличивается в зависимости от заданных <math>n</math> и <math>m</math> . | ||
| + | Очевидно, что каждый из первых <math>m</math> элементов представляется в виде одного числа. <math>(m+1)</math>-й элемент содержит <math>m</math> элементов, поскольку выражается через <math>m</math> элементов системы субмодулей: | ||
| + | |||
| + | :<math> a_{m+1} = (a_{m+1,1}, a_{m+1,2}, \ldots , a_{m+1,m}) </math>. | ||
| + | |||
| + | <math>(m+2)</math>-й элемент содержит <math>2 \cdot m</math> элементов, поскольку выражается через <math>m</math> элементов системы субмодулей и <math>m</math> элементов вектора <math> a_{m+1} </math> . Таким образом, продолжая рассуждения, можно заключить, что число элементов <math> L_i </math> для вектора <math> a_i </math> может быть выражено следующей формулой: | ||
| + | |||
| + | :<math>L_i = \begin{cases} | ||
| + | 1, & \mbox{if } i \le m ; \\ | ||
| + | 2^{i-m-1} \cdot m, & \mbox{if } m<i<n | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | Общее же число элементов<math> L </math>вектора <math> A </math> можно рассчитать, воспользовавшись формулой суммы геометрической прогрессии: | ||
| + | |||
| + | :<math>L = \sum_{i=1}^{n} L_i = m+m \cdot (2^0+2^1+ \ldots +2^{n-m+1}) = m \cdot (1+ \frac{2^{n-m}-1}{2-1}) = 2^{n-m} \cdot m </math> | ||
| + | |||
| + | |||
| + | Рассмотрим численный пример. Пусть задана система модулей: | ||
| + | <math> (p_1, p_2, p_3, p_4, p_5) = (2,3,5,29,863) </math>. | ||
| + | <math> P = 2 \cdot 3 \cdot 5 \cdot 29 \cdot 863 = 750810 </math>. | ||
| + | |||
| + | Также необходимо убедиться, что | ||
| + | <math> 2 \cdot 3 >5, 2 \cdot 3 \cdot 5 >29 </math>, <math> 2 \cdot 3 \cdot 5 \cdot 29 >863 </math>. | ||
| + | |||
| + | Выберем систему базовых модулей <math> (p_1, p_2) </math>. | ||
| + | В этом случае <math> Q = p_1 \cdot p_2 = 6 </math>, <math> n = 5, m = 2 </math>. | ||
| + | Число элементов вектора <math> L = 2^3 \cdot 2 = 16 </math>. | ||
| + | |||
| + | |||
| + | Разложим число <math> A = 865 </math>, заданное в позиционной системе счисления в вектор по обычному базису. | ||
| + | |||
| + | |||
| + | :<math> A = ( |865|_2, |865|_3, |865|_5, |865|_29, |865|_863 ) = ( 1, 1, 0, 24, 2 )</math>. | ||
| + | |||
| + | |||
| + | Теперь разложим число <math> A </math> по рекурсивному базису: | ||
| + | |||
| + | |||
| + | :<math> A = ( |865|_2, |865|_3, ( | |865|_5|_2, | |865|_5|_3 ), </math> | ||
| + | |||
| + | ::<math> ( | |865|_29|_2, | |865|_29|_3 , ( | | |865|_29|_5|_2, | | |865|_29|_5|_3 ) ) , </math> | ||
| + | |||
| + | ::<math> ( | |865|_863|_2, | |865|_863|_3 , ( | | |865|_863|_5|_2, | | |865|_863|_5|_3 ) ) , </math> | ||
| + | |||
| + | ::<math> ( | | |865|_863|_29|_2, | |865|_863|_29|_3 , </math> <math> ( | | | |865|_863|_29|_5|_2, | | | |865|_863|_29|_5|_3 ) ) ) ) </math>. | ||
| + | |||
| + | |||
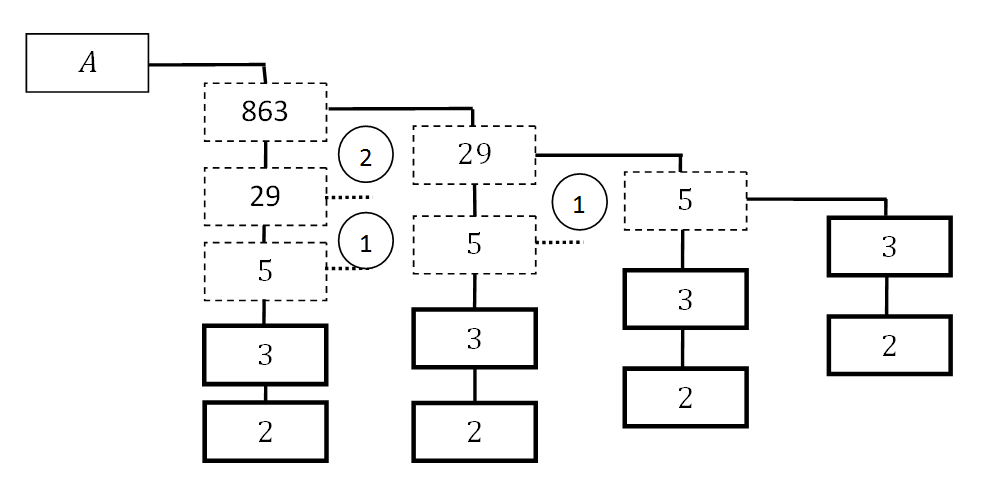
| + | Поскольку все числа в этом векторе не превышают 3, то для хранения вектора потребуется 16*2=32 бит вместо 20 бит для хранения числа в позиционной системе счисления. Степень избыточности составит 1.6. Иллюстрацию к примеру смотрите на рисунке 3. | ||
| + | |||
| + | |||
| + | [[изображение:RecModArith_03.png|frame|center|Рис.3. Разложение числа в системе (2,3,5,29,863) через систему базовых модулей (2,3)]] | ||
| + | |||
== Ограничения на выбор базиса == | == Ограничения на выбор базиса == | ||
| + | |||
| + | Максимальное значение, которое можно представить с помощью <math> P_{m+1} </math>, равно <math> max = p_{m+1} - 1 </math>. Чтобы была возможность выполнять арифметические операции над числами, требуется, чтобы результат операции для <math> p_{m+1} </math>-го элемента был меньше <math> Q = (p_1 \cdot p_2 \cdot \ldots \cdot p_m) </math>. Для сложения это будет <math> 2 \cdot max </math>, а для умножения - <math> max^2 </math>. | ||
| + | |||
| + | Рассмотрим следующий пример. Пусть задан базис <math> (2, 3, 5)</math>. Выберем систему базовых модулей <math> (2, 3)</math> . В этом случае <math> Q = 2 \cdot 3 = 6 </math>, <math> max = 4 </math>. Поскольку для сложения потребуется максимально представимое число 8, что больше 6, а для умножения 16, что тоже больше 6, то в таком базисе можно выполнять взаимно-однозначное разложение чисел, но для базовых арифметических операций он не подходит. Для реальных задач требуется увеличение числа <math> Q </math>. | ||
| + | |||
| + | Как именно выбирать элементы базиса? Рассмотрим следующий пример. | ||
| + | |||
| + | Пусть задана система базовых модулей <math> (4, 5, 7) </math>. Требуется определить <math> p_4 </math> таким образом, чтобы в рамках полученного рекурсивного базиса можно было использовать операцию умножения. | ||
| + | |||
| + | <math> Q > MAX </math> => <math> Q > max^2 </math> => <math> Q > (p_{4}-1)^2 </math> => <math> p_4 < \sqrt{Q} + 1 </math> => <math> p_4 < \sqrt{140} + 1 </math> => <math> p_4 < 12.8 </math>. | ||
| + | |||
| + | Следовательно, для реализации рекурсивного базиса мы можем выбрать <math> p_4 = 11 </math>. | ||
== Обратное преобразование числа из рекурсивного представления в позиционное == | == Обратное преобразование числа из рекурсивного представления в позиционное == | ||
| + | |||
| + | Для обратного представления также требуется рекурсивная реализация на базе того же метода, который используется для преобразования из вектора традиционной модулярной арифметики в позиционную систему счисления. | ||
| + | |||
| + | Пусть задан некоторый вектор <math> A = (a_1, a_2, \ldots , a_n) </math>. | ||
| + | |||
| + | Из свойств систем остаточных классов известно, что | ||
| + | : <math> A = (a_1, a_2, \ldots , a_n) = (a_1, 0, \ldots , 0) + (0, a_2, 0, \ldots , 0) + \ldots + (0, 0, \ldots , a_n) = |\sum_{i=1}^n{a_i \cdot b_i}| </math>, | ||
| + | где | ||
| + | :<math> B_0 = (1, 0, \ldots , 0) , B_1 = (0, 1, \ldots , 0) , \ldots , B_n = (0, 0, \ldots , 1) </math> - система ортогональных базисов. | ||
| + | |||
| + | В рекурсивной модулярной арифметике требуется найти набор ортогональных базисов для следующих систем остаточных классов: | ||
| + | :<math> (p_1, p_2, \ldots , p_m), (p_1, p_2, \ldots , p_{m+1}), \ldots + (p_1, p_2, \ldots , p_n) </math>. | ||
| + | |||
| + | |||
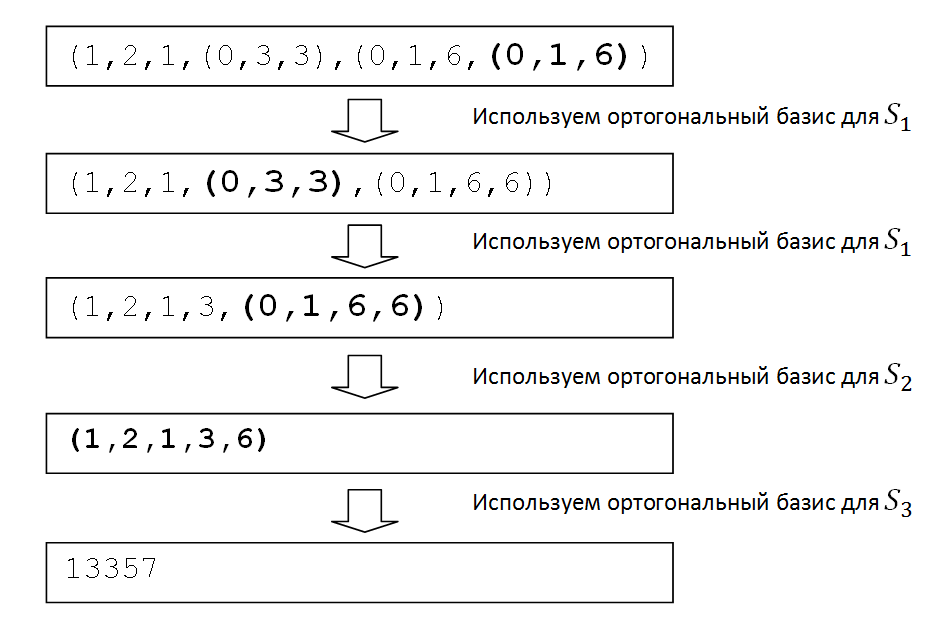
| + | Рассмотрим пример. Пусть задан базис <math> (3, 5, 7, 11, 13) </math> с системой базовых модулей <math> (3, 5, 7) </math>. И пусть требуется преобразовать вектор <math> (1, 2, 1, (0, 3, 3), (0, 1, 6, (0, 1, 6))) </math> в позиционную систему счисления. Для обратного преобразования требуется найти ортогональные базисы для каждой из следующих систем остаточных классов: | ||
| + | |||
| + | :<math> S_1 = (3, 5, 7) </math> => <math> B_{1,1} = (1, 0, 0) \equiv 70 </math>; <math> B_{1,2} = (0, 1, 0) \equiv 21 </math>; <math> B_{1,3} = (0, 0, 1) \equiv 15 </math>; | ||
| + | |||
| + | :<math> S_2 = (3, 5, 7, 11) </math> => <math> B_{2,1} \equiv 385 </math>; <math> B_{2,2} \equiv 231 </math>; <math> B_{2,3} \equiv 330 </math>; <math> B_{2,4} \equiv 210 </math>; | ||
| + | |||
| + | :<math> S_3 = (3, 5, 7, 11, 13) </math> => <math> B_{3,1} \equiv 5005 </math>; <math> B_{3,2} \equiv 6006 </math>; <math> B_{3,3} \equiv 10725 </math>; <math> B_{3,4} \equiv 1365 </math>; <math> B_{3,5} \equiv 6930 </math>; | ||
| + | |||
| + | Процесс обратного преобразования приведен на рисунке 4. В позиционной системе счисления искомый вектор равен 13357. | ||
| + | |||
| + | |||
| + | [[изображение:RecModArith_04.png|frame|center|Рис.4. Процесс обратного преобразования вектора]] | ||
| + | |||
== Сложение и умножение в рекурсивной модулярной арифметике == | == Сложение и умножение в рекурсивной модулярной арифметике == | ||
| + | |||
| + | Если выполнены ограничения, наложенные на базис, то сложение и умножение чисел выполняются так же, как и в традиционной модулярной арифметике. Чтобы сложить (умножить) два числа, требуется сложить (умножить) соответствующие элементы вектора по модулю <math> p_i </math>. А поскольку все элементы вектора имеют малую разрядность, параллельное сложение (умножение) выполняется очень быстро. | ||
Текущая версия на 13:35, 28 мая 2014
Содержание
Принцип рекурсивных модулярных вычислений
Система модулей традиционной модулярной арифметики может быть выражена через систему субмодулей меньшей размерности с использованием рекурсии.
Рекурсивная модулярная арифметика основана на принципе глубокого распараллеливания модульных операций модулярной арифметики с основаниями 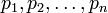 посредством сведения модульных операций по каждому рабочему основанию
посредством сведения модульных операций по каждому рабочему основанию 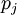 ,
, 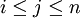 к модульным вычислениям по предшествующим рабочим основаниям
к модульным вычислениям по предшествующим рабочим основаниям 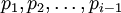 , имеющим то или иное технологическое преимущество (например, малобитным), которые называются базисными основаниями. Такая редукция допустима только при выполнении так называемого условия согласования вычислительных диапазонов по каждому рабочему модулю
, имеющим то или иное технологическое преимущество (например, малобитным), которые называются базисными основаниями. Такая редукция допустима только при выполнении так называемого условия согласования вычислительных диапазонов по каждому рабочему модулю 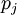 с вычислительными диапазонами по соответствующим комплексам базисных оснований.
с вычислительными диапазонами по соответствующим комплексам базисных оснований.
Принцип согласования гарантирует, во-первых, изоморфизм кольцевых операций по соответствующим им комплексам базисных оснований, и во-вторых, выполнимость обращения каждого шага рекурсии посредством перевода соответствующих модулярных кодов по базисным основаниям в позиционный код (например, на основе китайской теоремы об остатках, или переводом их в полиадический код).
Рекурсивное представление данных позволяет устранить некоторые недостатки модулярной арифметики. В частности, нивелируется неоднородность модульных вычислителей по сложности и времени выполнения операций. Несмотря на ограничения, которые накладываются на систему модулей, предложенный метод обеспечивает выигрыш по скорости и может быть применен в параллельных высокоскоростных вычислительных устройствах.
Пример
Поясним процедуру рекурсивных преобразований на простом примере. Возьмем в качестве базисных модулей двухбитные простые числа 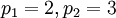 . Очевидно, что вычетами по модулям 2 и 3 можно однозначно представить любой вычет по модулю 5. В то же время вычетами по модулям 2, 3 и 5, где вычеты по модулю 5 представимы по модулям 2 и 3, можно однозначно представить любой вычет по модулю 29. Вычетами по модулям 2, 3, 5 и 29 можно однозначно представить любой вычет по модулю 863. И так далее пока не получим нужный набор рабочих оснований: 2, 3, 5, 29, 863,… Данный пример наглядно иллюстрирует 4 факта:
. Очевидно, что вычетами по модулям 2 и 3 можно однозначно представить любой вычет по модулю 5. В то же время вычетами по модулям 2, 3 и 5, где вычеты по модулю 5 представимы по модулям 2 и 3, можно однозначно представить любой вычет по модулю 29. Вычетами по модулям 2, 3, 5 и 29 можно однозначно представить любой вычет по модулю 863. И так далее пока не получим нужный набор рабочих оснований: 2, 3, 5, 29, 863,… Данный пример наглядно иллюстрирует 4 факта:
1) Аппаратные и временные затраты на представление чисел по базовым модулям 2 и 3 примерно одинаковы (оба базисных модуля двухбитные);
2) Наблюдается более высокая степень распараллеливаемости;
3) Появляется регулярность (все вычисления проводятся по модулям 2 и 3);
4) Столь малая разрядность базовых модулей позволяет эффективно реализовать модульные операции по базисным модулям в комбинационных схемах.
Однако имеется ряд ограничений, которые должны быть выполнены и которые приводят к усложнению устройств, созданных по данной методике. Рассмотрим эти ограничения.
Пусть есть система базисных модулей 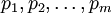 и необходимо представить вычеты по модулю
и необходимо представить вычеты по модулю 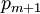 через вычеты по этой системе базовых модулей. Очевидно, что максимальный вычет по модулю
через вычеты по этой системе базовых модулей. Очевидно, что максимальный вычет по модулю 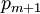 равен
равен 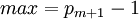 . Зная это значение и последовательность выполняемых операций, можно рассчитать максимальное значение
. Зная это значение и последовательность выполняемых операций, можно рассчитать максимальное значение 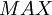 результата арифметической операции. Очевидно, что для однозначного представления результата арифметических операций необходимо, чтобы
результата арифметической операции. Очевидно, что для однозначного представления результата арифметических операций необходимо, чтобы 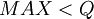 , где
, где 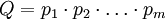 . Для остальных модулей расчет производится аналогично.
. Для остальных модулей расчет производится аналогично.
Для примера с базовыми модулями 2 и 3 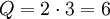 . Наименьшее простое число (после 2 и 3) - это 5, следовательно,
. Наименьшее простое число (после 2 и 3) - это 5, следовательно, 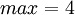 .
Нельзя выполнить ни операцию сложения, т.к.
.
Нельзя выполнить ни операцию сложения, т.к. 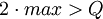
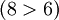 , ни, тем более, операцию умножения, т.к.
, ни, тем более, операцию умножения, т.к. 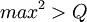
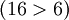 .
Чтобы выполнять любую из арифметических операций (сложение или умножение) надо увеличить число
.
Чтобы выполнять любую из арифметических операций (сложение или умножение) надо увеличить число 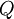 (т.е. увеличить значения базисных модулей и/или их количество).
(т.е. увеличить значения базисных модулей и/или их количество).
Возьмем в качестве базисных модулей все взаимно простые трехбитные числа: 4, 5 и 7. В этом случае 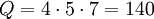 .
.
Таким образом, выбираем 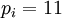 (ближайшее к 7 простое число). Далее совокупность рабочих модулей строится с помощью аналогичного расчета, пока не будет достигнут требуемый вычислительный диапазон.
(ближайшее к 7 простое число). Далее совокупность рабочих модулей строится с помощью аналогичного расчета, пока не будет достигнут требуемый вычислительный диапазон.
Наконец, рассмотрим реальный случай. Пусть нам нужно реализовать преобразователь Фурье для 24-битных аргументов при количестве точек 1024.
Для этого потребуется вычислять сумму 1024 произведений, т.е. обеспечить 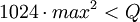 . Здесь уже не обойтись системой только трехбитных базисных модулей. Добавим к ним четырехбитные: 5, 7, 8, 9, 11 и 13 (Q = 360360).
Для выбора ближайшего рабочего модуля необходимо
. Здесь уже не обойтись системой только трехбитных базисных модулей. Добавим к ним четырехбитные: 5, 7, 8, 9, 11 и 13 (Q = 360360).
Для выбора ближайшего рабочего модуля необходимо 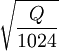 .
.
Получаем 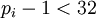 .
Выбираем
.
Выбираем 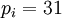 .
.
Аналогичным расчетом реализуем рекурсивное дерево рабочих оснований целиком.
Чтобы сделать такое устройство, нужно спроектировать блок из 6 вычислителей (для каждого базисного модуля), потребуется 16 таких блоков. Вот где работает регулярность.
Заметим, что все вычислители будут иметь высокую скорость модульных операций (суперраспараллеливание) и небольшие аппаратные затраты в силу малости базисных модулей или их близости к степеням двойки.
Таким образом, предложенный аппарат рекурсивных модулярных вычислений дает следующие преимущества:
- 1. Устранение дисбаланса в операциях с малыми и большими модулями (аппаратные и временные затраты примерно одинаковы, т.к. в идеале все базисные модули имеют одинаковое число бит).
- 2. Существенно более высокая степень распараллеливаемости, а значит и более высокое быстродействие.
- 3. Появляется регулярность (большое количество одинаковых базисных модулей).
- 4. Малая разрядность базисных модулей позволяет реализовать модульные операции на комбинационных схемах, оптимизированных в базисе булевых функций.
Представление данных и основные операции рекурсивной модулярной арифметики
Идея, на которой базируется рекурсивная модулярная арифметика: выразить систему модулей через систему субмодулей, имеющую меньшую размерность.
Пусть задана система модулей 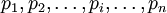 и задан некоторый вектор
и задан некоторый вектор 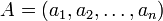 . Выразим
. Выразим 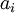 через систему субмодулей
через систему субмодулей
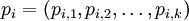 , где
, где 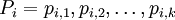 и
и 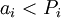 :
: 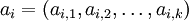 .
.
В этом случае вектор A можно представить в следующем виде:
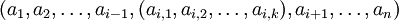 , см. рисунок 1.
, см. рисунок 1.
Назовем систему из m младших модулей системой базовых модулей, а их произведение обозначим 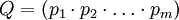 .
.
Пусть 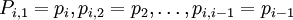 , а
, а 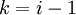 , тогда при
, тогда при 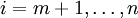 имеет место рекурсия.
имеет место рекурсия. 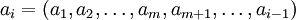 по системе модулей
по системе модулей 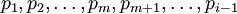 или, раскрывая рекурсию:
или, раскрывая рекурсию: 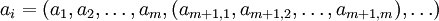 . На рис.2 приведен частный случай разложения элемента
. На рис.2 приведен частный случай разложения элемента 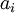 для случая
для случая 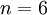 и
и 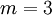 .
.
Прямое преобразование числа из позиционной системы счисления в представление рекурсивной модулярной арифметики
Если в традиционной модулярной арифметике число элементов вектора равно числу элементов в системе модулей, то в рекурсивной модулярной арифметике количество элементов вектора увеличивается в зависимости от заданных  и
и  .
Очевидно, что каждый из первых
.
Очевидно, что каждый из первых  элементов представляется в виде одного числа.
элементов представляется в виде одного числа. 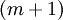 -й элемент содержит
-й элемент содержит  элементов, поскольку выражается через
элементов, поскольку выражается через  элементов системы субмодулей:
элементов системы субмодулей:
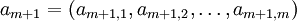 .
.
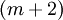 -й элемент содержит
-й элемент содержит 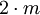 элементов, поскольку выражается через
элементов, поскольку выражается через  элементов системы субмодулей и
элементов системы субмодулей и  элементов вектора
элементов вектора 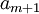 . Таким образом, продолжая рассуждения, можно заключить, что число элементов
. Таким образом, продолжая рассуждения, можно заключить, что число элементов 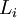 для вектора
для вектора 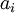 может быть выражено следующей формулой:
может быть выражено следующей формулой:
Общее же число элементов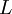 вектора
вектора  можно рассчитать, воспользовавшись формулой суммы геометрической прогрессии:
можно рассчитать, воспользовавшись формулой суммы геометрической прогрессии:
Рассмотрим численный пример. Пусть задана система модулей:
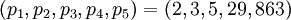 .
.
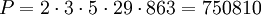 .
.
Также необходимо убедиться, что
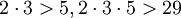 ,
, 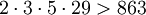 .
.
Выберем систему базовых модулей 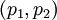 .
В этом случае
.
В этом случае 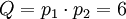 ,
, 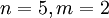 .
Число элементов вектора
.
Число элементов вектора 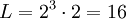 .
.
Разложим число 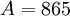 , заданное в позиционной системе счисления в вектор по обычному базису.
, заданное в позиционной системе счисления в вектор по обычному базису.
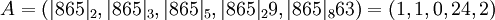 .
.
Теперь разложим число  по рекурсивному базису:
по рекурсивному базису:
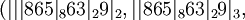
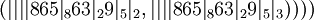 .
.
Поскольку все числа в этом векторе не превышают 3, то для хранения вектора потребуется 16*2=32 бит вместо 20 бит для хранения числа в позиционной системе счисления. Степень избыточности составит 1.6. Иллюстрацию к примеру смотрите на рисунке 3.
Ограничения на выбор базиса
Максимальное значение, которое можно представить с помощью 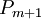 , равно
, равно 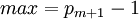 . Чтобы была возможность выполнять арифметические операции над числами, требуется, чтобы результат операции для
. Чтобы была возможность выполнять арифметические операции над числами, требуется, чтобы результат операции для 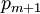 -го элемента был меньше
-го элемента был меньше 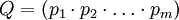 . Для сложения это будет
. Для сложения это будет 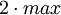 , а для умножения -
, а для умножения - 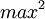 .
.
Рассмотрим следующий пример. Пусть задан базис 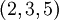 . Выберем систему базовых модулей
. Выберем систему базовых модулей 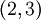 . В этом случае
. В этом случае 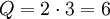 ,
, 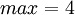 . Поскольку для сложения потребуется максимально представимое число 8, что больше 6, а для умножения 16, что тоже больше 6, то в таком базисе можно выполнять взаимно-однозначное разложение чисел, но для базовых арифметических операций он не подходит. Для реальных задач требуется увеличение числа
. Поскольку для сложения потребуется максимально представимое число 8, что больше 6, а для умножения 16, что тоже больше 6, то в таком базисе можно выполнять взаимно-однозначное разложение чисел, но для базовых арифметических операций он не подходит. Для реальных задач требуется увеличение числа 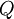 .
.
Как именно выбирать элементы базиса? Рассмотрим следующий пример.
Пусть задана система базовых модулей 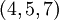 . Требуется определить
. Требуется определить 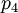 таким образом, чтобы в рамках полученного рекурсивного базиса можно было использовать операцию умножения.
таким образом, чтобы в рамках полученного рекурсивного базиса можно было использовать операцию умножения.
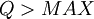 =>
=> 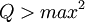 =>
=> 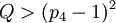 =>
=> 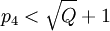 =>
=> 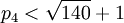 =>
=> 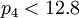 .
.
Следовательно, для реализации рекурсивного базиса мы можем выбрать 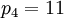 .
.
Обратное преобразование числа из рекурсивного представления в позиционное
Для обратного представления также требуется рекурсивная реализация на базе того же метода, который используется для преобразования из вектора традиционной модулярной арифметики в позиционную систему счисления.
Пусть задан некоторый вектор 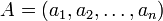 .
.
Из свойств систем остаточных классов известно, что
-
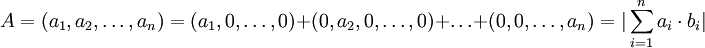 ,
,
где
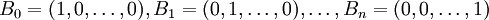 - система ортогональных базисов.
- система ортогональных базисов.
В рекурсивной модулярной арифметике требуется найти набор ортогональных базисов для следующих систем остаточных классов:
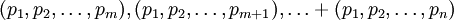 .
.
Рассмотрим пример. Пусть задан базис 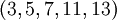 с системой базовых модулей
с системой базовых модулей 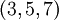 . И пусть требуется преобразовать вектор
. И пусть требуется преобразовать вектор 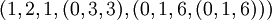 в позиционную систему счисления. Для обратного преобразования требуется найти ортогональные базисы для каждой из следующих систем остаточных классов:
в позиционную систему счисления. Для обратного преобразования требуется найти ортогональные базисы для каждой из следующих систем остаточных классов:
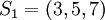 =>
=> 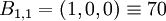 ;
; 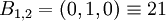 ;
; 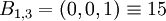 ;
;
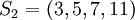 =>
=> 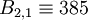 ;
; 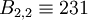 ;
; 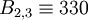 ;
; 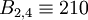 ;
;
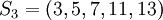 =>
=> 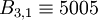 ;
; 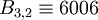 ;
; 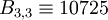 ;
; 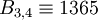 ;
; 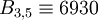 ;
;
Процесс обратного преобразования приведен на рисунке 4. В позиционной системе счисления искомый вектор равен 13357.
Сложение и умножение в рекурсивной модулярной арифметике
Если выполнены ограничения, наложенные на базис, то сложение и умножение чисел выполняются так же, как и в традиционной модулярной арифметике. Чтобы сложить (умножить) два числа, требуется сложить (умножить) соответствующие элементы вектора по модулю 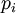 . А поскольку все элементы вектора имеют малую разрядность, параллельное сложение (умножение) выполняется очень быстро.
. А поскольку все элементы вектора имеют малую разрядность, параллельное сложение (умножение) выполняется очень быстро.