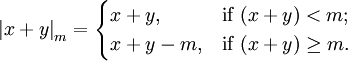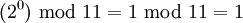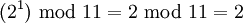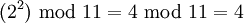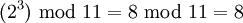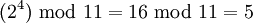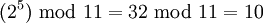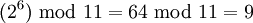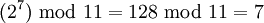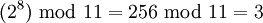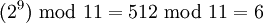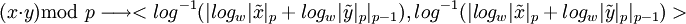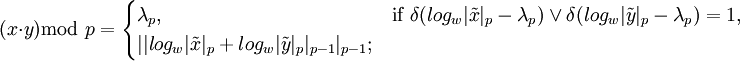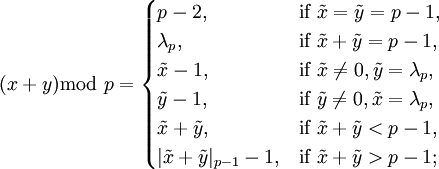Бимодульная модулярная арифметика — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| (не показано 18 промежуточных версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | Аддитивный характер вычислений в кольце вычетов <math> Z_p </math> порождает дополнительные расходы на выполнение арифметических операций. Это обусловлено тем, что результат выполненной операции может выйти за диапазон <math> Z_p </math>, тогда требуется корректировка результата, т.е. взятие результата выполненной операции по модулю. Мультипликативная операция над остатками x, y mod p более трудоемка, поэтому наиболее эффективным способом избежать прямой реализации мультипликативной операции является переход к индексам вычетов по основанию первообразного корня, однозначно связанных с данным модулярным кодом. | + | Аддитивный характер вычислений в кольце вычетов <math> Z_p </math> порождает дополнительные расходы на выполнение арифметических операций. Это обусловлено тем, что результат выполненной операции может выйти за диапазон <math> Z_p </math>, тогда требуется корректировка результата, т.е. взятие результата выполненной операции по модулю. Мультипликативная операция над остатками <math> x, y \text{ mod }p </math> более трудоемка, поэтому наиболее эффективным способом избежать прямой реализации мультипликативной операции является переход к индексам вычетов по основанию первообразного корня, однозначно связанных с данным модулярным кодом. |
| − | В случае индексной арифметики операция «+» выполняется за один такт модульного суммирования, а операция «*» за такт модульного суммирования и два такта табличной операции. | + | В случае индексной арифметики операция «+» выполняется за один такт модульного суммирования, а операция «*» за такт модульного суммирования и два такта табличной операции. Бимодульная модулярная арифметика направлена на то, чтобы сбалансировать выполнение модульных операций. |
| − | = Кодовая конструкция проф. Д.А. Поспелова = | + | == Кодовая конструкция проф. Д.А. Поспелова == |
| − | + | Д.А. Поспелов ввел представление исходных операндов в виде пар <math> <|x|_p, ind_w|x|_p> </math>, где <math> |x|_p </math> есть вычет <math> x </math> по модулю <math> p </math>, <math> i = ind_w|x|_p </math> - соответствующий вычету <math> |x|_p </math> индекс по основанию <math> w </math> (см. [[Модулярная логарифметика]]), при этом условно считается, что вычету 0 соответствует специальный символ <math> \lambda </math> (обозначается также <math> inf </math>), который обладает свойством <math> \lambda+i=i+\lambda </math> для любого для любого индекса <math> 0\le i\le p-2 </math>. Таким образом, все операции поля выполняются над парами чисел. | |
| − | + | Если требуется найти сумму двух операндов по модулю <math> p </math>, то суммируются по модулю <math> p </math> первые компоненты пар; для формирования второй компоненты пары результата этот результат преобразуется в индекс путем выборки значения из таблицы индексов (рис.1): | |
| − | = Модифицированная кодовая конструкция = | + | [[изображение:BimodModArith_fig1_add.JPG|200px|frame|left|Рис.1. Структурная схема операции сложения]] |
| + | |||
| + | <br style="clear:both" /> | ||
| + | |||
| + | Если требуется найти произведение двух операндов по модулю <math> p </math>, то суммируются по модулю <math> p - 1 </math> вторые компоненты пар; для формирования первой компоненты пары результата этот результат преобразуется в антилогарифм (вычет) путем выборки значения из таблицы вычетов (рис.2): | ||
| + | |||
| + | [[изображение:BimodModArith_fig2_mult.JPG|200px|frame|left|Рис.2. Структурная схема операции умножения]] | ||
| + | |||
| + | <br style="clear:both" /> | ||
| + | |||
| + | Арифметику, построенную на парном представлении операндов, будем называть бимодульной арифметикой поля <math> GF(p)</math>. | ||
| + | |||
| + | Таким образом, операции сложения и умножения сведены к операциям сложения по модулю <math> p </math> и модулю <math> p-1 </math>, соответственно, и одной табличной операции выбора второй компоненты пары результата. Такое решение позволяет сократить время выполнения мультипликативной операции на один такт табличной операции и площадь на хранение двух таблиц преобразования в индексы, размерность каждой таблицы <math>2(p-1)</math>. При этом, Д.А. Поспелов утверждает [1, стр. 296], что, несмотря на то, что логика операции умножения по модулю <math> p </math> стала более сложной, чем в обычной системе кода в остатках, выигрыш состоит в «однотипности оборудования для производства операций сложения и умножения». Данное утверждение справедливо в общем случае, когда сумматоры по модулям <math> p </math> и <math> (p-1) </math> проектируются по методу прямой логической реализации с использованием двоичных функциональных блоков. В этом случае суммирование по модулю <math> m </math> для двух операндов <math> x </math> и <math> y </math>, находящихся в диапазоне <math>{0, 1,\ldots, m-1}</math>, выполняется по следующей формуле: | ||
| + | |||
| + | :<math>{|x+y|}_m = \begin{cases} | ||
| + | x+y, & \mbox{if } (x+y) < m ; \\ | ||
| + | x+y-m, & \mbox{if } (x+y) \ge m. | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | == Пример == | ||
| + | |||
| + | Пусть надо выполнить сложение и умножение: | ||
| + | :<math> sum = (a+b) \text{ mod } p </math>, | ||
| + | :<math> prod = (a*b) \text{ mod } p </math>, | ||
| + | где | ||
| + | :<math> 0 <= a < p </math>, | ||
| + | :<math> 0 <= b < p </math>, | ||
| + | <math> p </math> – простое число, | ||
| + | <math> \text{ mod } p </math> – операция нахождения остатка по модулю. | ||
| + | |||
| + | |||
| + | Рассмотрим пример для модуля <math> p = 11 </math>. Первообразный корень <math> w </math> для этого значения модуля равен 2. А именно, возведение <math> w </math> в степень 0, 1, … 9 дает неповторяющиеся результаты: | ||
| + | |||
| + | :<math> (2^0) \text{ mod } 11 = 1 \text{ mod } 11 = 1 </math> | ||
| + | :<math> (2^1) \text{ mod } 11 = 2 \text{ mod } 11 = 2 </math> | ||
| + | :<math> (2^2) \text{ mod } 11 = 4 \text{ mod } 11 = 4 </math> | ||
| + | :<math> (2^3) \text{ mod } 11 = 8 \text{ mod } 11 = 8 </math> | ||
| + | :<math> (2^4) \text{ mod } 11 = 16 \text{ mod } 11 = 5 </math> | ||
| + | :<math> (2^5) \text{ mod } 11 = 32 \text{ mod } 11 = 10 </math> | ||
| + | :<math> (2^6) \text{ mod } 11 = 64 \text{ mod } 11 = 9 </math> | ||
| + | :<math> (2^7) \text{ mod } 11 = 128 \text{ mod } 11 = 7 </math> | ||
| + | :<math> (2^8) \text{ mod } 11 = 256 \text{ mod } 11 = 3 </math> | ||
| + | :<math> (2^9) \text{ mod } 11 = 512 \text{ mod } 11 = 6 </math> | ||
| + | |||
| + | |||
| + | Для получения таблицы преобразования между обычным и индексным представлением расположим полученные пары значений в порядке возрастания. Для модуля <math> p = 11 </math> таблицы будет выглядеть следующим образом. | ||
| + | |||
| + | |||
| + | Таблица прямого преобразования: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | Число ||1||2||3||4||5||6||7||8||9||10 | ||
| + | |- | ||
| + | | Индекс ||0||1||8||2||4||9||7||3||6||5 | ||
| + | |} | ||
| + | |||
| + | |||
| + | Таблица обратного преобразования: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | Индекс ||0||1||2||3||4||5||6||7||8||9 | ||
| + | |- | ||
| + | | Число ||1||2||4||8||5||10||9||7||3||6 | ||
| + | |} | ||
| + | |||
| + | |||
| + | В качестве примера возьмем числа 8 и 6. Эти числа представляются парами <8,3> и <6,9>. | ||
| + | |||
| + | Найдем значение выражения (8+6) mod 11 обычным образом. Это первое число пары, представляющей результат сложения. (8+6) mod 11 = 14 mod 11 = 3. По таблице прямого преобразования находим, что числу 3 соответствует значение индекса 8. Это второе число пары. Итак. | ||
| + | :<math> <sum, ind_2 {(sum)}> = <8,3> + <6,9> = <3,8> </math>. | ||
| + | |||
| + | Найдем значение выражения (8*6) mod 11 используя средства логарифметики. Числа 8 и 6 имеют соответствующие индексы 3 и 9 (см. таблицу прямого преобразования). Просуммировав эти индексы по модулю (11-1) = 10 получим результат (3+9) mod 10 = 12 mod 10 = 2. Это второе число пары, представляющей результат умножения. По таблице обратного преобразования находим для индекса 2 конечный результат, равный 4. Это первое число пары. Итак, | ||
| + | :<math> <prod, ind_2 {(prod)}> = <8,3> * <6,9> = <4,2> </math>. | ||
| + | |||
| + | |||
| + | == Модифицированная кодовая конструкция == | ||
| + | |||
| + | Рассмотренный метод построения сумматоров по модулю, во-первых, позволяет в полной мере использовать современные наработки в области проектирования двоичных устройств, во-вторых, предоставляет большую гибкость при реализации каждого компонента в составе всего вычислительного блока в зависимости от требований к занимаемой площади и быстродействию. В-третьих, метод универсален, т.е. независим от специфики используемого базового модуля m. | ||
| + | |||
| + | Однако в настоящее время все большую популярность завоевывают гибридные методы построения базовых арифметических узлов модулярной арифметики. Такие методы представляют собой комбинацию методов прямой логической реализации и методов на основе таблиц состояний. Использование гибридных методов обеспечивает компромисс между быстродействием и затратами на занимаемую площадь для некоторых значений модулей. В случае же реализации арифметики в кодах Д.А. Поспелова требуется оценивать проектирование сумматоров не только относительно базового модуля <math> p </math>, но и модуля <math> p-1 </math>, иначе теряется основная идея данного кодирования, а именно, однотипность оборудования. | ||
| + | |||
| + | Следующая модификация кода Д.А. Поспелова развивает его идею однотипности. | ||
| + | Развитие идеи однотипности состоит в том, чтобы аддитивные и мультипликативные операции модульной арифметики выполнялись не только аппаратно однотипно, но и однотипно в кодовом представлении операндов. Это достигается путем перехода от предствления компонент пар операндов по модулям <math> p </math> и <math> p-1 </math> к однородному представлению по модулю <math> p-1 </math>. | ||
| + | |||
| + | |||
| + | Введем понятие модифицированного вычета по модулю: | ||
| + | |||
| + | :<math> {|\tilde x|}_p = {\lambda}_p \cdot \delta \cdot ((p-1)-|x|_p) + {||x|_p|}_{p-1} \cdot {\hat \delta} \cdot ((p-1)-|x|_p)</math>, | ||
| + | |||
| + | где | ||
| + | |||
| + | :<math> {\delta}(u) = \begin{cases} | ||
| + | 1, & \mbox{if } u=0, \\ | ||
| + | 0, & \mbox{if } u\ne 0, | ||
| + | \end{cases} | ||
| + | </math> - функция Кронекера , | ||
| + | |||
| + | |||
| + | :<math> {\hat \delta}(u) = 1-{\delta}(u) </math> - кофункция Кронекера. | ||
| + | |||
| + | |||
| + | Для представления второй компоненты пары операнда будем использовать дискретно-логарифметическое представление. Этот способ представления является эффективным при использовании небольших значений модулей порядка 8 бит, что является достаточным при проектировании большинства вычислительных устройств, предназначенных для решения специальных задач из области применения модулярной арифметики. Тем самым вторая компонента пары операндов будет иметь вид: | ||
| + | |||
| + | :<math> log_w{|\tilde x|}_p = \delta({|\tilde x|}_p) \cdot {\lambda}_p + {\hat \delta}({|\tilde x|}_p) \cdot ind_w (x_p)</math> , где | ||
| + | |||
| + | :<math> ind_w|{\tilde x}|_p </math> - индекс вычета <math> |{\tilde x}|_p </math> по основанию <math> w </math>, т.е. | ||
| + | |||
| + | :<math> |{\tilde x}|_p \ne 0 \Leftrightarrow |{w^{ind_w|{\tilde x}|_p}| = |{\tilde x}|_p} </math> . | ||
| + | |||
| + | В этом случае полагается, что при <math> t </math>-битном простом числе <math> p </math> константный символ <math> {\lambda}_p = 2^t-1 </math>. Очевидно, что при любом простом <math> p </math> <math> {\lambda}_p \notin Z_{p-1} </math> . | ||
| + | |||
| + | Распишем, как в бимодульной арифметике будут выполняться арифметические операции. | ||
| + | |||
| + | Реализация мультипликативных операций останется без изменений: | ||
| + | |||
| + | если | ||
| + | |||
| + | :<math> <|{\tilde x}|_{p}, log_w{|{\tilde x}|}_p> </math>, <math> <|{\tilde y}|_{p}, log_w{|{\tilde y}|}_p> </math>, | ||
| + | |||
| + | то | ||
| + | |||
| + | :<math> (x \cdot y) \text{mod }p \longrightarrow < log^{-1} (|{log_w|{\tilde x}|_p + log_w|{\tilde y}|_p}|_{p-1}), log^{-1} (|{log_w|{\tilde x}|_p + log_w|{\tilde y}|_p}|_{p-1}) > </math> | ||
| + | |||
| + | |||
| + | т.е. | ||
| + | |||
| + | :<math>(x \cdot y) \text{mod }p = \begin{cases} | ||
| + | {\lambda}_p, & \mbox{if } {\delta(log_w|{\tilde x}|_p - {\lambda}_p})\vee {\delta(log_w|{\tilde y}|_p - {\lambda}_p}) = 1, \\ | ||
| + | ||{log_w|{\tilde x}|_p + log_w|{\tilde y}|_p}|_{p-1}|_{p-1} ; | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Логика выполнения аддитивных операций усложнится за счет введения дополнительных логических функций, связанных с переходом к однородному представлению. Аддитивные операции выполняются согласно выражению: | ||
| + | |||
| + | если | ||
| + | |||
| + | :<math> <|{\tilde x}|_{p}, log_w{|{\tilde x}|}_p> </math>, <math> <|{\tilde y}|_{p}, log_w{|{\tilde y}|}_p> </math>, | ||
| + | |||
| + | то | ||
| + | |||
| + | :<math> (x + y) \text{mod }p \longrightarrow < |{\tilde x} + {\tilde y}|_{p-1} , log_w(|{\tilde x} + {\tilde y}|_{p-1}) > </math>, | ||
| + | |||
| + | |||
| + | т.е. | ||
| + | |||
| + | :<math>(x + y) \text{mod }p = \begin{cases} | ||
| + | p-2, & \mbox{if } {\tilde x} = {\tilde y} = p-1 , \\ | ||
| + | {\lambda}_p, & \mbox{if } {\tilde x} + {\tilde y} = p-1 , \\ | ||
| + | {\tilde x}-1, & \mbox{if } {\tilde x}\ne 0 , {\tilde y} = {\lambda}_p , \\ | ||
| + | {\tilde y}-1, & \mbox{if } {\tilde y}\ne 0 , {\tilde x} = {\lambda}_p , \\ | ||
| + | {\tilde x} + {\tilde y}, & \mbox{if } {\tilde x} + {\tilde y} < p-1 , \\ | ||
| + | |{\tilde x} + {\tilde y}|_{p-1}-1, & \mbox{if } {\tilde x} + {\tilde y} > p-1 ; | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Тем самым, переход к однородному представлению операндов позволил выполнять аддитивные и мультипликативные операции на одном оборудовании, а именно на сумматоре по модулю <math> p-1 </math>. Это положительно влияет и на требования к затратам по занимаемой площади и на контроль выполнения арифметических операций, при этом сохраняется требование однотипности используемого оборудования. | ||
| + | |||
| + | |||
| + | == Ссылки == | ||
| + | |||
| + | * [1] Поспелов Д.А. Арифметические основы вычислительных машин дискретного действия. М.: Высш. шк., 1970. | ||
Текущая версия на 13:57, 18 июня 2014
Аддитивный характер вычислений в кольце вычетов 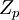 порождает дополнительные расходы на выполнение арифметических операций. Это обусловлено тем, что результат выполненной операции может выйти за диапазон
порождает дополнительные расходы на выполнение арифметических операций. Это обусловлено тем, что результат выполненной операции может выйти за диапазон 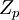 , тогда требуется корректировка результата, т.е. взятие результата выполненной операции по модулю. Мультипликативная операция над остатками
, тогда требуется корректировка результата, т.е. взятие результата выполненной операции по модулю. Мультипликативная операция над остатками 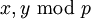 более трудоемка, поэтому наиболее эффективным способом избежать прямой реализации мультипликативной операции является переход к индексам вычетов по основанию первообразного корня, однозначно связанных с данным модулярным кодом.
более трудоемка, поэтому наиболее эффективным способом избежать прямой реализации мультипликативной операции является переход к индексам вычетов по основанию первообразного корня, однозначно связанных с данным модулярным кодом.
В случае индексной арифметики операция «+» выполняется за один такт модульного суммирования, а операция «*» за такт модульного суммирования и два такта табличной операции. Бимодульная модулярная арифметика направлена на то, чтобы сбалансировать выполнение модульных операций.
Содержание
Кодовая конструкция проф. Д.А. Поспелова
Д.А. Поспелов ввел представление исходных операндов в виде пар 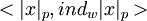 , где
, где 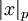 есть вычет
есть вычет  по модулю
по модулю  ,
, 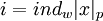 - соответствующий вычету
- соответствующий вычету 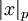 индекс по основанию
индекс по основанию 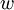 (см. Модулярная логарифметика), при этом условно считается, что вычету 0 соответствует специальный символ
(см. Модулярная логарифметика), при этом условно считается, что вычету 0 соответствует специальный символ 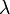 (обозначается также
(обозначается также 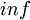 ), который обладает свойством
), который обладает свойством 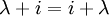 для любого для любого индекса
для любого для любого индекса 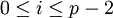 . Таким образом, все операции поля выполняются над парами чисел.
. Таким образом, все операции поля выполняются над парами чисел.
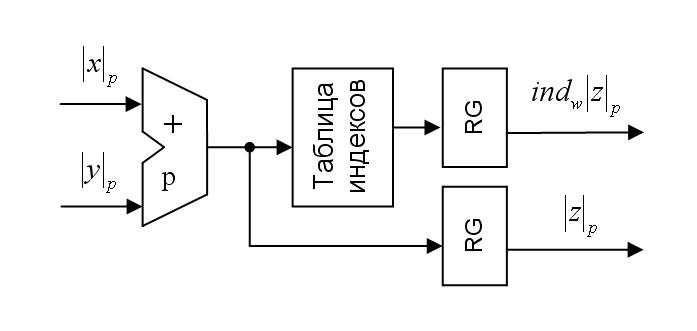
Если требуется найти сумму двух операндов по модулю  , то суммируются по модулю
, то суммируются по модулю  первые компоненты пар; для формирования второй компоненты пары результата этот результат преобразуется в индекс путем выборки значения из таблицы индексов (рис.1):
первые компоненты пар; для формирования второй компоненты пары результата этот результат преобразуется в индекс путем выборки значения из таблицы индексов (рис.1):
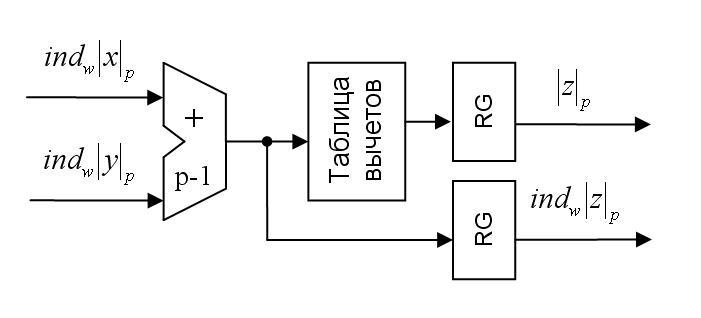
Если требуется найти произведение двух операндов по модулю  , то суммируются по модулю
, то суммируются по модулю 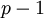 вторые компоненты пар; для формирования первой компоненты пары результата этот результат преобразуется в антилогарифм (вычет) путем выборки значения из таблицы вычетов (рис.2):
вторые компоненты пар; для формирования первой компоненты пары результата этот результат преобразуется в антилогарифм (вычет) путем выборки значения из таблицы вычетов (рис.2):
Арифметику, построенную на парном представлении операндов, будем называть бимодульной арифметикой поля 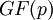 .
.
Таким образом, операции сложения и умножения сведены к операциям сложения по модулю  и модулю
и модулю 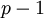 , соответственно, и одной табличной операции выбора второй компоненты пары результата. Такое решение позволяет сократить время выполнения мультипликативной операции на один такт табличной операции и площадь на хранение двух таблиц преобразования в индексы, размерность каждой таблицы
, соответственно, и одной табличной операции выбора второй компоненты пары результата. Такое решение позволяет сократить время выполнения мультипликативной операции на один такт табличной операции и площадь на хранение двух таблиц преобразования в индексы, размерность каждой таблицы 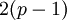 . При этом, Д.А. Поспелов утверждает [1, стр. 296], что, несмотря на то, что логика операции умножения по модулю
. При этом, Д.А. Поспелов утверждает [1, стр. 296], что, несмотря на то, что логика операции умножения по модулю  стала более сложной, чем в обычной системе кода в остатках, выигрыш состоит в «однотипности оборудования для производства операций сложения и умножения». Данное утверждение справедливо в общем случае, когда сумматоры по модулям
стала более сложной, чем в обычной системе кода в остатках, выигрыш состоит в «однотипности оборудования для производства операций сложения и умножения». Данное утверждение справедливо в общем случае, когда сумматоры по модулям  и
и 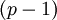 проектируются по методу прямой логической реализации с использованием двоичных функциональных блоков. В этом случае суммирование по модулю
проектируются по методу прямой логической реализации с использованием двоичных функциональных блоков. В этом случае суммирование по модулю  для двух операндов
для двух операндов  и
и 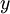 , находящихся в диапазоне
, находящихся в диапазоне 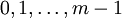 , выполняется по следующей формуле:
, выполняется по следующей формуле:
Пример
Пусть надо выполнить сложение и умножение:
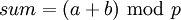 ,
,
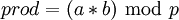 ,
,
где
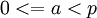 ,
,
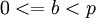 ,
,
 – простое число,
– простое число,
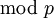 – операция нахождения остатка по модулю.
– операция нахождения остатка по модулю.
Рассмотрим пример для модуля 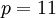 . Первообразный корень
. Первообразный корень 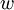 для этого значения модуля равен 2. А именно, возведение
для этого значения модуля равен 2. А именно, возведение 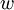 в степень 0, 1, … 9 дает неповторяющиеся результаты:
в степень 0, 1, … 9 дает неповторяющиеся результаты:
Для получения таблицы преобразования между обычным и индексным представлением расположим полученные пары значений в порядке возрастания. Для модуля 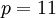 таблицы будет выглядеть следующим образом.
таблицы будет выглядеть следующим образом.
Таблица прямого преобразования:
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Индекс | 0 | 1 | 8 | 2 | 4 | 9 | 7 | 3 | 6 | 5 |
Таблица обратного преобразования:
| Индекс | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Число | 1 | 2 | 4 | 8 | 5 | 10 | 9 | 7 | 3 | 6 |
В качестве примера возьмем числа 8 и 6. Эти числа представляются парами <8,3> и <6,9>.
Найдем значение выражения (8+6) mod 11 обычным образом. Это первое число пары, представляющей результат сложения. (8+6) mod 11 = 14 mod 11 = 3. По таблице прямого преобразования находим, что числу 3 соответствует значение индекса 8. Это второе число пары. Итак.
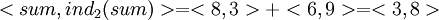 .
.
Найдем значение выражения (8*6) mod 11 используя средства логарифметики. Числа 8 и 6 имеют соответствующие индексы 3 и 9 (см. таблицу прямого преобразования). Просуммировав эти индексы по модулю (11-1) = 10 получим результат (3+9) mod 10 = 12 mod 10 = 2. Это второе число пары, представляющей результат умножения. По таблице обратного преобразования находим для индекса 2 конечный результат, равный 4. Это первое число пары. Итак,
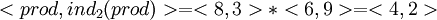 .
.
Модифицированная кодовая конструкция
Рассмотренный метод построения сумматоров по модулю, во-первых, позволяет в полной мере использовать современные наработки в области проектирования двоичных устройств, во-вторых, предоставляет большую гибкость при реализации каждого компонента в составе всего вычислительного блока в зависимости от требований к занимаемой площади и быстродействию. В-третьих, метод универсален, т.е. независим от специфики используемого базового модуля m.
Однако в настоящее время все большую популярность завоевывают гибридные методы построения базовых арифметических узлов модулярной арифметики. Такие методы представляют собой комбинацию методов прямой логической реализации и методов на основе таблиц состояний. Использование гибридных методов обеспечивает компромисс между быстродействием и затратами на занимаемую площадь для некоторых значений модулей. В случае же реализации арифметики в кодах Д.А. Поспелова требуется оценивать проектирование сумматоров не только относительно базового модуля  , но и модуля
, но и модуля 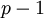 , иначе теряется основная идея данного кодирования, а именно, однотипность оборудования.
, иначе теряется основная идея данного кодирования, а именно, однотипность оборудования.
Следующая модификация кода Д.А. Поспелова развивает его идею однотипности.
Развитие идеи однотипности состоит в том, чтобы аддитивные и мультипликативные операции модульной арифметики выполнялись не только аппаратно однотипно, но и однотипно в кодовом представлении операндов. Это достигается путем перехода от предствления компонент пар операндов по модулям  и
и 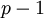 к однородному представлению по модулю
к однородному представлению по модулю 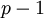 .
.
Введем понятие модифицированного вычета по модулю:
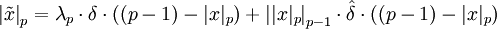 ,
,
где
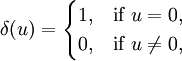 - функция Кронекера ,
- функция Кронекера ,
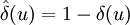 - кофункция Кронекера.
- кофункция Кронекера.
Для представления второй компоненты пары операнда будем использовать дискретно-логарифметическое представление. Этот способ представления является эффективным при использовании небольших значений модулей порядка 8 бит, что является достаточным при проектировании большинства вычислительных устройств, предназначенных для решения специальных задач из области применения модулярной арифметики. Тем самым вторая компонента пары операндов будет иметь вид:
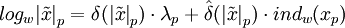 , где
, где
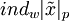 - индекс вычета
- индекс вычета 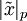 по основанию
по основанию 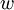 , т.е.
, т.е.
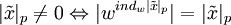 .
.
В этом случае полагается, что при 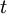 -битном простом числе
-битном простом числе  константный символ
константный символ 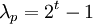 . Очевидно, что при любом простом
. Очевидно, что при любом простом 
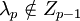 .
.
Распишем, как в бимодульной арифметике будут выполняться арифметические операции.
Реализация мультипликативных операций останется без изменений:
если
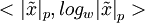 ,
, 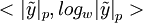 ,
,
то
т.е.
Логика выполнения аддитивных операций усложнится за счет введения дополнительных логических функций, связанных с переходом к однородному представлению. Аддитивные операции выполняются согласно выражению:
если
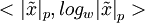 ,
, 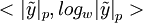 ,
,
то
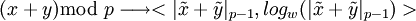 ,
,
т.е.
Тем самым, переход к однородному представлению операндов позволил выполнять аддитивные и мультипликативные операции на одном оборудовании, а именно на сумматоре по модулю 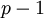 . Это положительно влияет и на требования к затратам по занимаемой площади и на контроль выполнения арифметических операций, при этом сохраняется требование однотипности используемого оборудования.
. Это положительно влияет и на требования к затратам по занимаемой площади и на контроль выполнения арифметических операций, при этом сохраняется требование однотипности используемого оборудования.
Ссылки
- [1] Поспелов Д.А. Арифметические основы вычислительных машин дискретного действия. М.: Высш. шк., 1970.