Модулярная логарифметика — различия между версиями
Материал из Модулярная арифметики
Turbo (обсуждение | вклад) (Новая страница: «'''Модулярная логарифметика''' (более полное название '''Логарифмическая система остаточн…») |
Turbo (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
'''Модулярная логарифметика''' (более полное название '''Логарифмическая система остаточных классов''', в английском варианте '''The Residue Logarithmic Number System''') - система счисления основанная на [[Система остаточных классов|системе остаточных классов]], в которой числа представлены в виде дискретных логарифмов от соответствующих вычетов. | '''Модулярная логарифметика''' (более полное название '''Логарифмическая система остаточных классов''', в английском варианте '''The Residue Logarithmic Number System''') - система счисления основанная на [[Система остаточных классов|системе остаточных классов]], в которой числа представлены в виде дискретных логарифмов от соответствующих вычетов. | ||
| + | |||
| + | == Первообразный корень == | ||
| + | |||
| + | Первообразным корнем <math>w</math> по модулю <math>p</math> (другое название примитивный корень) называется целое число, возведение, которого в степень <math>0, 1, 2, ..., (p-2)</math> дает неповторяющиеся вычеты по модулю <math>p</math>. | ||
| + | |||
| + | == Дискретный логарифм == | ||
| + | |||
| + | Пусть <math>w</math> – первообразный корень конечного поля <math>GF(p)</math>. Дискретным логарифмом по основанию <math>w</math> над <math>GF(p)</math> будем называть функцию аргумента <math>x</math>, заданную формулой: | ||
Версия 14:20, 3 июня 2013
Модулярная логарифметика (более полное название Логарифмическая система остаточных классов, в английском варианте The Residue Logarithmic Number System) - система счисления основанная на системе остаточных классов, в которой числа представлены в виде дискретных логарифмов от соответствующих вычетов.
Первообразный корень
Первообразным корнем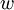 
по модулю 
(другое название примитивный корень) называется целое число, возведение, которого в степень 
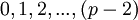дает неповторяющиеся вычеты по модулю .
Дискретный логарифм
Пусть 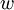– первообразный корень конечного поля 
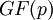. Дискретным логарифмом по основанию 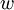над 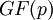будем называть функцию аргумента 
, заданную формулой:
