Описание КТО III — различия между версиями
Материал из Модулярная арифметики
Turbo (обсуждение | вклад) (Новая страница: «== Китайская теорема об остатках "третьей версии"== Третья версия теоремы [1] является расш…») |
Turbo (обсуждение | вклад) |
||
| Строка 2: | Строка 2: | ||
Третья версия теоремы [1] является расширением [[Описание КТО II|второй версии]] на системы модулей, не являющиеся взаимнопростыми, то есть на избыточную систему остаточных классов. | Третья версия теоремы [1] является расширением [[Описание КТО II|второй версии]] на системы модулей, не являющиеся взаимнопростыми, то есть на избыточную систему остаточных классов. | ||
| + | |||
| + | Система модулей <math>S = (m_1, m_2, \dots, m_n)</math> не является взаимно простой если <math>HOD(m_i, m_j) > 1</math> для некоторых <math>i j</math>. Динамический диапазон для такой системы модулей равен <math>M = HOK(m_1, m_2, \dots, m_n)</math>. | ||
| + | |||
== Ссылки == | == Ссылки == | ||
[1] OPTIMIZATION OF NEW CHINESE REMAINDER THEOREMS USING SPECIAL MODULI SETS | [1] OPTIMIZATION OF NEW CHINESE REMAINDER THEOREMS USING SPECIAL MODULI SETS | ||
Версия 06:24, 19 июня 2013
Китайская теорема об остатках "третьей версии"
Третья версия теоремы [1] является расширением второй версии на системы модулей, не являющиеся взаимнопростыми, то есть на избыточную систему остаточных классов.
Система модулей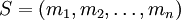 
не является взаимно простой если 
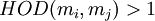для некоторых 
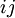. Динамический диапазон для такой системы модулей равен 
.
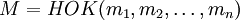Ссылки
[1] OPTIMIZATION OF NEW CHINESE REMAINDER THEOREMS USING SPECIAL MODULI SETS
