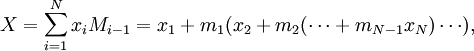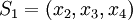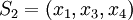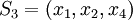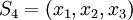Полиадический код — различия между версиями
Turbo (обсуждение | вклад) |
Turbo (обсуждение | вклад) |
||
| Строка 50: | Строка 50: | ||
== Коррекция ошибок на базе полиадического кода == | == Коррекция ошибок на базе полиадического кода == | ||
| − | Пусть задан набор модулей <math>(p_1, p_2, p_3, p_4)</math>, где <math>(p_1 < p_2 < p_3 < p_4)</math>. Из них первые два <math>(p_1, p_2)</math> являются информационными, а последние два <math>(p_3, p_4)</math> - проверочными. | + | Пусть задан набор модулей <math>(p_1, p_2, p_3, p_4)</math>, где <math>(p_1 < p_2 < p_3 < p_4)</math>. Из них первые два <math>(p_1, p_2)</math> являются информационными, а последние два <math>(p_3, p_4)</math> - проверочными. Данный набор позволяет корректировать одиночную ошибку в одном из модулярных каналов. Для коррекции можно использовать следующий наиболее простой подход: из модулярного представления числа <math>(x_1, x_2, x_3, x_4)</math> последовательно исключается каждый канал, формируя наборы: |
| + | * <math>S_1 = (x_2, x_3, x_4)</math> | ||
| + | * <math>S_2 = (x_1, x_3, x_4)</math> | ||
| + | * <math>S_3 = (x_1, x_2, x_4)</math> | ||
| + | * <math>S_4 = (x_1, x_2, x_3)</math> | ||
| + | |||
| + | Динамический диапазон каждой из троек превышает заданный (можно убедиться для каждой тройки: <math>p_1 \cdot p_2 \cdot p_3 > p_1 \cdot p_2</math>). В случае если ошибок не было, то при обратном преобразовании в позиционное представление значения всех троек должны лежать в диапазоне: <math>[0 <= X < p_1 \cdot p_2]</math> и быть равными. В случае, если в одном из каналов произошла ошибка, то правильное значение даст только одна тройка, в которой исключено неверное значение, все остальные тройки будут лежать вне динамического диапазона ('''здесь нужна ссылка на пруФФФФФ или сам пруф'''). | ||
| + | |||
| + | В этом случае для восстановления числа требуется сделать 4 обратных преобразователя для каждой из троек. Сравнить полученные значения с <math>p_1 \cdot p_2</math> и на основании сравнения выдать на выход правильное значение. Однако как будет показано ниже преобразователь можно значительно сократить по площади, объединив одинаковые части в каждом из обратных преобразователей и рассчитывая финальное позиционное значение только один раз для тройки с правильным значением [2]. | ||
== Ссылки == | == Ссылки == | ||
* [1] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York. | * [1] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York. | ||
* [2] [https://docs.google.com/viewer?url=patentimages.storage.googleapis.com/pdfs/US4752904.pdf Патент "Efficient structure for computing mixed-radix projections from residue number systems"] | * [2] [https://docs.google.com/viewer?url=patentimages.storage.googleapis.com/pdfs/US4752904.pdf Патент "Efficient structure for computing mixed-radix projections from residue number systems"] | ||
Версия 17:36, 25 сентября 2013
Содержание
Введение
Полиадический код (или система счисления со смешанным основанием от англ. associated mixed radix system (AMRS))
Любое число 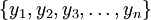 в системе остаточных классов может быть представленно в виде полиадического кода
в системе остаточных классов может быть представленно в виде полиадического кода
где
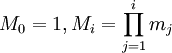 для
для 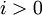 и
и 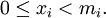
Полиадический код используется для:
- Сравнения чисел
- Перевода чисел из системы остаточных классов в обычную позиционную систему счисления
Обратное преобразование
Обратное преобразование на базе полиадического кода, базируется на идее, что любое число X может быть представлено в системе взаимно простых чисел 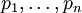 , как [1]:
, как [1]:
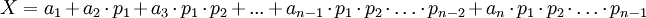 , где
, где 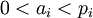
-
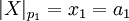
-
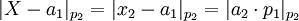 =>
=> 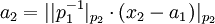
-
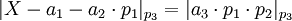 =>
=> 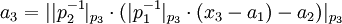
-
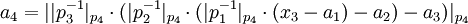
- ...
-
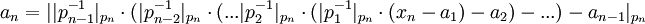
Для использования этого метода требуются константы вида 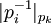 . Можно также заметить, что начинать вычисление
. Можно также заметить, что начинать вычисление 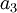 можно, как только появилось значение
можно, как только появилось значение 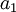 . На основе этого метода можно строить конвейерные преобразователи.
. На основе этого метода можно строить конвейерные преобразователи.
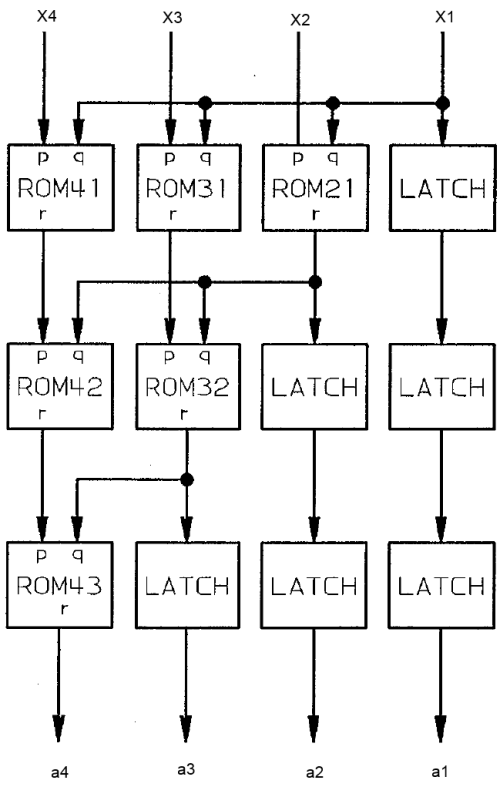
Конвейерный преобразователь в полиадический код
Используя формулы выше можно нарисовать схему конвейерного преобразователя. В данном случае мы используем модулярный базис из 4 элементов:
- ROMij - это таблица выполняющая следующее преобразование
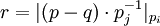 . Для больших значений модулей таблица может быть заменена на последовательный набор арифметических операций (вычитание, умножение на константу и взятие модуля)
. Для больших значений модулей таблица может быть заменена на последовательный набор арифметических операций (вычитание, умножение на константу и взятие модуля)
- LATCH - элемент памяти сохраняющий значение до следующего такта
- На преобразование модулярного представления в полиадический код требуется N-1 ступеней конвейера.
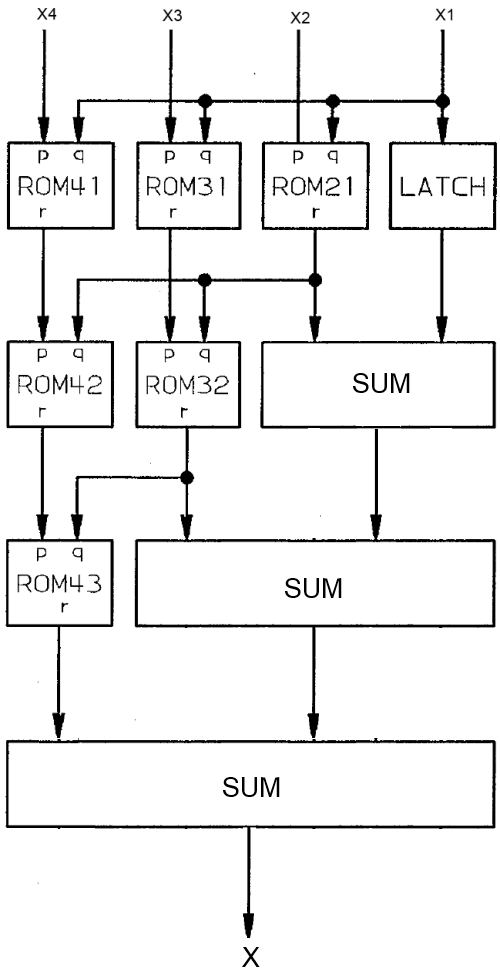
Обратный конвейерный преобразователь на базе полиадического кода
Этот преобразователь используется для восстановления числа 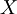 из модулярного кода, заданного набором остатков
из модулярного кода, заданного набором остатков 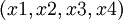 .
.
- ROMij - это таблица выполняющая следующее преобразование
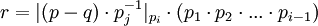 . Для больших значений модулей таблица может быть заменена на последовательный набор арифметических операций (вычитание, умножение на константу и взятие модуля)
. Для больших значений модулей таблица может быть заменена на последовательный набор арифметических операций (вычитание, умножение на константу и взятие модуля)
- LATCH - элемент памяти сохраняющий значение до следующего такта
- SUM - обычный сумматор
- На преобразование модулярного представления в позиционный вид требуется N ступеней конвейера.
- В отличие от преобразования в полиадический код, данный преобразователь получается более громоздким из-за более сложной структуры ROMij и наличия сумматоров, битовый размер которых растет в нижней части конвейера.
Коррекция ошибок на базе полиадического кода
Пусть задан набор модулей 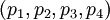 , где
, где 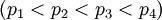 . Из них первые два
. Из них первые два 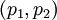 являются информационными, а последние два
являются информационными, а последние два 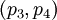 - проверочными. Данный набор позволяет корректировать одиночную ошибку в одном из модулярных каналов. Для коррекции можно использовать следующий наиболее простой подход: из модулярного представления числа
- проверочными. Данный набор позволяет корректировать одиночную ошибку в одном из модулярных каналов. Для коррекции можно использовать следующий наиболее простой подход: из модулярного представления числа 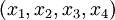 последовательно исключается каждый канал, формируя наборы:
последовательно исключается каждый канал, формируя наборы:
Динамический диапазон каждой из троек превышает заданный (можно убедиться для каждой тройки: 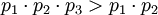 ). В случае если ошибок не было, то при обратном преобразовании в позиционное представление значения всех троек должны лежать в диапазоне:
). В случае если ошибок не было, то при обратном преобразовании в позиционное представление значения всех троек должны лежать в диапазоне: ![[0 <= X < p_1 \cdot p_2]](/w/images/math/7/5/6/756279094b6aca9ba967803c6f3bd159.png) и быть равными. В случае, если в одном из каналов произошла ошибка, то правильное значение даст только одна тройка, в которой исключено неверное значение, все остальные тройки будут лежать вне динамического диапазона (здесь нужна ссылка на пруФФФФФ или сам пруф).
и быть равными. В случае, если в одном из каналов произошла ошибка, то правильное значение даст только одна тройка, в которой исключено неверное значение, все остальные тройки будут лежать вне динамического диапазона (здесь нужна ссылка на пруФФФФФ или сам пруф).
В этом случае для восстановления числа требуется сделать 4 обратных преобразователя для каждой из троек. Сравнить полученные значения с 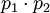 и на основании сравнения выдать на выход правильное значение. Однако как будет показано ниже преобразователь можно значительно сократить по площади, объединив одинаковые части в каждом из обратных преобразователей и рассчитывая финальное позиционное значение только один раз для тройки с правильным значением [2].
и на основании сравнения выдать на выход правильное значение. Однако как будет показано ниже преобразователь можно значительно сократить по площади, объединив одинаковые части в каждом из обратных преобразователей и рассчитывая финальное позиционное значение только один раз для тройки с правильным значением [2].
Ссылки
- [1] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York.
- [2] Патент "Efficient structure for computing mixed-radix projections from residue number systems"