Описание работы универсального прямого преобразователя — различия между версиями
Turbo (обсуждение | вклад) (Новая страница: «== Описание работы универсального прямого преобразователя из позиционного представлени…») |
Turbo (обсуждение | вклад) |
||
| Строка 3: | Строка 3: | ||
== Постановка задачи == | == Постановка задачи == | ||
| − | Требуется реализовать микроэлектронное устройство выполняющее преобразование из позиционного представления в модулярный код. Разработку будем вести на языке Verilog. Пусть задано входное число <math>X</math> в позиционном виде разрядности <math>N</math>-бит. Требуется найти остаток от его деления на каждое число из набора, образующих модулярный базис <math>{p1, p2, ... pN}</math>. Так как алгоритм вычисления остатков будет одинаков для каждого из них, то рассмотрим произвольное число <math>p</math> размерности <math>k</math>-бит. | + | Требуется реализовать микроэлектронное устройство выполняющее преобразование из позиционного представления в модулярный код. Разработку будем вести на языке Verilog. Пусть задано входное число <math>X</math> в позиционном виде разрядности <math>N</math>-бит. Требуется найти остаток от его деления (вычет) на каждое число из набора, образующих модулярный базис <math>{p1, p2, ... pN}</math>. Так как алгоритм вычисления остатков будет одинаков для каждого из них, то рассмотрим произвольное число из набора <math>p</math> размерности <math>k</math>-бит. |
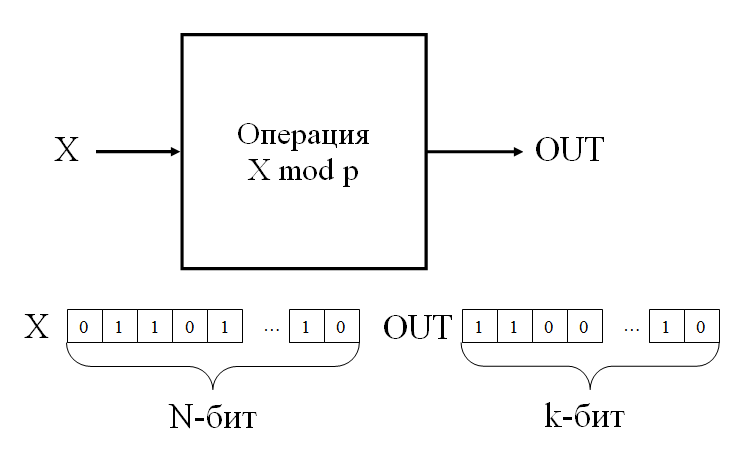
Схема этого блока с входами и выходами: | Схема этого блока с входами и выходами: | ||
| Строка 13: | Строка 13: | ||
* <math>0 \le OUT < p</math> | * <math>0 \le OUT < p</math> | ||
* <math>p</math> - константа заданная на этапе проектирования | * <math>p</math> - константа заданная на этапе проектирования | ||
| + | |||
| + | == Специальные случаи == | ||
| + | |||
| + | При некоторых соотношениях между входными данными и заданным p, модуль взятия остатка от деления можно реализовать простейшим образом. Рассмотрим такие случаи: | ||
| + | |||
| + | === Модуль больше входных данных === | ||
| + | |||
| + | <math>p > 2^N</math> - в этом случае выходные данные совпадают с входными, то есть <math>OUT = X</math>. | ||
| + | |||
| + | |||
| + | <source lang="verilog" line> | ||
| + | module forward_conv_module_23 (in, out); | ||
| + | input [3:0] in; // Max value: 15 | ||
| + | output [4:0] out; // Max value: 22 | ||
| + | assign out = {1'd0,in[3:0]}; | ||
| + | endmodule | ||
| + | </source> | ||
| + | |||
| + | === Модуль равен степени двойки === | ||
| + | |||
| + | <math>p = 2^t</math> - в этом случае выходные данные равны младшим t-бит входных данных, то есть <math>OUT = X[t:0]</math>. | ||
| + | |||
| + | |||
| + | <source lang="verilog" line> | ||
| + | module forward_conv_module_16 (out0, in); | ||
| + | output [3:0] out0; // Max value: 15 | ||
| + | input [7:0] in; // Max value: 255 | ||
| + | assign out0 = in[3:0]; | ||
| + | endmodule | ||
| + | </source> | ||
| + | |||
| + | === N незначительно превосходит разрядность модуля === | ||
| + | |||
| + | В этом случае достаточно проверить в какой из диапазонов вида <math>[0;p), [p;2 \cdot p), [2 \cdot p;3 \cdot p), ...</math> попадает <math>X</math> и вычесть из него поправочный коэффициент, соответствующий диапазону. <math>0</math> для <math>[0;p)</math>, <math>p</math> для <math>[p;2 \cdot p)</math>, <math>2 \cdot p</math> для <math>[p;2 \cdot p)</math> и.т.д. | ||
| + | |||
| + | |||
| + | <source lang="verilog" line> | ||
| + | module mod_253_511 (in, out); | ||
| + | input [8:0] in; | ||
| + | output reg [7:0] out; | ||
| + | always @ (in) | ||
| + | begin | ||
| + | if (in < 8'd253) | ||
| + | begin | ||
| + | out = in; | ||
| + | end | ||
| + | else if (in < 9'd506) | ||
| + | begin | ||
| + | out = in - 8'd253; | ||
| + | end | ||
| + | else | ||
| + | begin | ||
| + | out = in - 9'd506; | ||
| + | end | ||
| + | end | ||
| + | endmodule | ||
| + | |||
| + | module forward_conv_module_253 (in, out); | ||
| + | input [8:0] in; // Max value: 511 | ||
| + | output [7:0] out; // Max value: 252 | ||
| + | mod_253_511 inst(in, out); | ||
| + | endmodule | ||
| + | </source> | ||
Версия 16:42, 29 ноября 2013
Содержание
Описание работы универсального прямого преобразователя из позиционного представления в модулярный код
Постановка задачи
Требуется реализовать микроэлектронное устройство выполняющее преобразование из позиционного представления в модулярный код. Разработку будем вести на языке Verilog. Пусть задано входное число 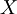 в позиционном виде разрядности
в позиционном виде разрядности 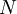 -бит. Требуется найти остаток от его деления (вычет) на каждое число из набора, образующих модулярный базис
-бит. Требуется найти остаток от его деления (вычет) на каждое число из набора, образующих модулярный базис 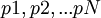 . Так как алгоритм вычисления остатков будет одинаков для каждого из них, то рассмотрим произвольное число из набора
. Так как алгоритм вычисления остатков будет одинаков для каждого из них, то рассмотрим произвольное число из набора  размерности
размерности 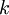 -бит.
-бит.
Схема этого блока с входами и выходами:
Здесь:
-
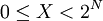
-
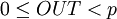
-
 - константа заданная на этапе проектирования
- константа заданная на этапе проектирования
Специальные случаи
При некоторых соотношениях между входными данными и заданным p, модуль взятия остатка от деления можно реализовать простейшим образом. Рассмотрим такие случаи:
Модуль больше входных данных
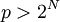 - в этом случае выходные данные совпадают с входными, то есть
- в этом случае выходные данные совпадают с входными, то есть 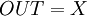 .
.
module forward_conv_module_23 (in, out);
input [3:0] in; // Max value: 15
output [4:0] out; // Max value: 22
assign out = {1'd0,in[3:0]};
endmodule
Модуль равен степени двойки
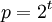 - в этом случае выходные данные равны младшим t-бит входных данных, то есть
- в этом случае выходные данные равны младшим t-бит входных данных, то есть ![OUT = X[t:0]](/w/images/math/8/e/8/8e8f19c11f52113a6c70c26019ae3c55.png) .
.
module forward_conv_module_16 (out0, in);
output [3:0] out0; // Max value: 15
input [7:0] in; // Max value: 255
assign out0 = in[3:0];
endmodule
N незначительно превосходит разрядность модуля
В этом случае достаточно проверить в какой из диапазонов вида 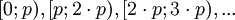 попадает
попадает 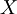 и вычесть из него поправочный коэффициент, соответствующий диапазону.
и вычесть из него поправочный коэффициент, соответствующий диапазону. 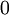 для
для 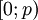 ,
,  для
для 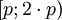 ,
, 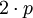 для
для 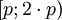 и.т.д.
и.т.д.
module mod_253_511 (in, out);
input [8:0] in;
output reg [7:0] out;
always @ (in)
beginif (in < 8'd253)
beginout = in;
endelse if (in < 9'd506)
beginout = in - 8'd253;
endelsebeginout = in - 9'd506;
endendendmodulemodule forward_conv_module_253 (in, out);
input [8:0] in; // Max value: 511
output [7:0] out; // Max value: 252
mod_253_511 inst(in, out);
endmodule