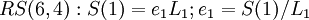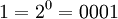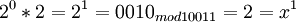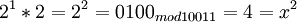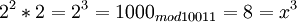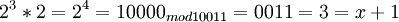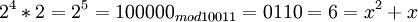Участник:Nikz — различия между версиями
NikZ (обсуждение | вклад) |
NikZ (обсуждение | вклад) |
||
| Строка 159: | Строка 159: | ||
где <math>X_1,X_2,..,X_i</math> - локаторы ошибок<br /> | где <math>X_1,X_2,..,X_i</math> - локаторы ошибок<br /> | ||
Ясно, что если этот многочлен будет найден, то мы легко сможем определить локаторы ошибок – для этого потребуется только определить его корни.<br /> | Ясно, что если этот многочлен будет найден, то мы легко сможем определить локаторы ошибок – для этого потребуется только определить его корни.<br /> | ||
| − | Для определения этого полинома сначала получают вспомогательный полином <math>S(x)</math>, так называемый синдром ошибки. Коэффициенты синдрома ошибки получаются подстановкой степеней примитивного члена в остаток многочлен <math>r(x)=C(x)mod g(x)</math><br /> | + | Для определения этого полинома сначала получают вспомогательный полином <math>S(x)</math>, так называемый синдром ошибки. Коэффициенты синдрома ошибки получаются подстановкой степеней примитивного члена в остаток многочлен <math>r(x) = C(x) mod g(x)</math>: <math>S_i=e(a^{i})</math><br /> |
| − | <math> | + | Между <math>L(x)</math> и <math>S(x)</math> существует соотношение<br /> |
| + | <math>L(x)S(x)=W(x)modx^{N-K}</math><br /> | ||
| + | <math>W(x)</math> называется многочленом ошибок. Степень многочлена <math>W(x)</math> не может превышать <math>t-1</math>, где <math>t</math> – количество ошибок, то есть в максимальном случае <math>(N-K)/2-1</math><br /> | ||
| + | С учётом этого обстоятельства, а также учитывая, что свободный член <math>L(x): L_0=1</math> (ведь <math>L(x)=(1+xX_1 )(1+xX_2 )..(1+xX_i) )</math> можно составить систему линейных уравнений. | ||
| + | <math>W(x)=</math><br /> | ||
| + | <math>L_0 S_0</math><br /> | ||
| + | <math>(L_0 S_1+L_1 S_0 )X+</math><br /> | ||
| + | <math>(L_0 S_2+L_1 S_1+L_2 S_0 ) X^2+</math><br /> | ||
| + | <math>(L_0 S_3+L_1 S_2+L_2 S_1+L_3 S_0 ) X^3+</math><br /> | ||
| + | <math>...</math><br /> | ||
| + | <math>(L_0 S_{N-K-1}+L_1 S_{N-K-2}..L_{(N-K)/2} S_{(N-K)/2-1}X^{N-K-1}</math><br /> | ||
| + | Пусть <math>t = (N-K)/2</math><br /> | ||
| + | Коэффициенты при степенях от 0 до t – 1 не равны нулю, при старших степенях должны быть нулевыми.<br /> | ||
| + | <math>L_0 S_t+L_1 S_{t-1}+L_2 S_{t-2}+L_3 S_{t-3}...L_t S_0 = 0</math><br /> | ||
| + | <math>L_0 S_{t+1}+L_1 S_t+L_2 S_{t-1}+L_3 S_{t-2}...L_t S_1 = 0</math><br /> | ||
| + | <math>L_0 S_{t+2}+L_1 S_{t+1}+L_2 S_t+L_3 S_{t-1}...L_t S_2 = 0</math><br /> | ||
| + | <math>\dots</math><br /> | ||
| + | <math>L_0 S_{2t-1}+L_1 S_{2t-2}+L_2 S_{2t-3}+L_3 S_{2t-4}...L_t S_t = 0</math><br /> | ||
| + | Коэффициент <math>L_0</math> известен, остальные необходимо найти, следовательно требуется составить t уравнений.<br /> | ||
| + | <math>L_1 S_{t-1}+L_2 S_{t-2}+L_3 S_{t-3}...L_t S_0 = S_t</math><br /> | ||
| + | <math>L_1 S_t+L_2 S_{t-1}+L_3 S_{t-2}...L_t S_1 = S_{t+1}</math><br /> | ||
| + | <math>L_1 S_{t+1}+L_2 S_t+L_3 S_{t-1}...L_t S_2 = S_{t+2}</math><br /> | ||
| + | <math>...</math><br /> | ||
| + | <math>L_1 S_{2t-2}+L_2 S_{2t-3}+L_3 S_{2t-4}...L_t S_t = S_{2t-1}</math><br /> | ||
| + | В матричном виде:<br /> | ||
| + | |||
| + | <math>M= | ||
| + | \quad\left\|\begin{array}{ccccc} | ||
| + | S_{t-1} & S_{t-2} & S_{t-3} & \cdots & S_0\\ | ||
| + | S_{t} & S_{t-1} & S_{t-2} & \cdots & S_1\\ | ||
| + | S_{t+1} & S_{t} & S_{t-1} & \cdots & S_2\\ | ||
| + | \cdots & \cdots & \cdots & \cdots & \cdots \\ | ||
| + | S_{2t-2} & S_{2t-3} & S_{2t-4} & \cdots & S_t\\ | ||
| + | \end{array}\right\|</math><br /><br /> | ||
| + | <math>V=\quad\left\|\begin{array}{c} | ||
| + | S_{t} \\ | ||
| + | S_{t+1} \\ | ||
| + | S_{t+2} \\ | ||
| + | \cdots \\ | ||
| + | S_{2t-1} \\ | ||
| + | \end{array}\right\|</math><br /><br /> | ||
| + | <math>L=\quad\left\|\begin{array}{c} | ||
| + | L_{1} \\ | ||
| + | L_{2} \\ | ||
| + | L_{3} \\ | ||
| + | \cdots \\ | ||
| + | L_{t} \\ | ||
| + | \end{array}\right\|</math><br /><br /> | ||
| + | <math>ML = V, \Rightarrow M^{-1}V</math> | ||
| + | Например, для нашего примера – кода Рида-Соломона (6, 4) матрица M имеет вид:<br /> | ||
| + | <math> M = S_1</math> , а вектор <math>V = S_2; </math> <math> L(1) = S(2) / S(1)</math><br /> | ||
| + | Таким образом, вычисление полинома локаторов сводится к построению матрицы M, нахождению обратной ей и умножению на вектор V. | ||
| + | Обратная матрица получается так же, как и в обычной математике, например Жордановым методом. | ||
| + | После того, как полином <math>L(x)</math> найден, следует найти его корни – они будут обратны к локаторам ошибок. <br /> | ||
| + | После нахождения позиции ошибки,займемся нахождением значением ошибки:<br /> | ||
| + | Воспользуемся определением синдромной функции:<br /> | ||
| + | <math>S(1) = r(\alpha) = e_1 L_1 + e_2 L_2 + ... + e_n L_n</math>,<br /> где <math>e_1,e_2,..,e_n - </math>значение ошибки. <math>L_1,L_2,..,L_n - </math>позиция ошибки.<br /> | ||
| + | Для нашего кода <math>RS(6,4): S(1) = e_1 L_1; e_1 = S(1) / L_1</math> | ||
Версия 15:21, 16 июня 2014
Содержание
Пример коррекции ошибки с помощью кодов Рида - Соломона
Постановка задачи
В данной статье разбирается пример работы алгоритма коррекции ошибки для 16-битных строк. Строка разбивает на блоки длиной 4 бита и каждый блок представляет собой элемент поля Галуа GF16. Необходимо отследить и исправить одиночную ошибку, внесённую в один из блоков.
Теоретические основы алгоритма
Поля Галуа
Операцию сложения определим как "исключающее ИЛИ" 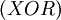 .Очевидно, что в таком случае операция сложения является обратной самой себе. Тогда операция умножения в двоичном виде будет выглядеть так:
.Очевидно, что в таком случае операция сложения является обратной самой себе. Тогда операция умножения в двоичном виде будет выглядеть так:

Так можно умножать полиномы, в данном случае мы умножили:
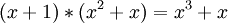 .
Определим также операцию деления чисел(или полиномов) с остатком – по аналогичным правилам, например:
.
Определим также операцию деления чисел(или полиномов) с остатком – по аналогичным правилам, например:
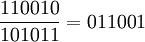 или
или 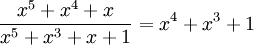 Теперь построим поле из 16 элементов
Теперь построим поле из 16 элементов 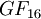 . Операцию сложения определена на XOR, Операция деления дополнена получением остатка по некоторому модулю.
Выберем в качестве модуля неприводимый полином
. Операцию сложения определена на XOR, Операция деления дополнена получением остатка по некоторому модулю.
Выберем в качестве модуля неприводимый полином 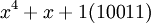 .
.
Возьмем единицу и будем последовательно умножать ее на 2 и рассмотрим числа, которые будут при этом
и так далее.
Составим таблицу умножения
| Степень | Результат | |
|---|---|---|
| 0 | 1 | 0001 |
| 1 | 2 | 0010 |
| 2 | 4 | 0100 |
| 3 | 8 | 1000 |
| 4 | 3 | 0011 |
| 5 | 6 | 0110 |
| 6 | 12 | 1100 |
| 7 | 11 | 1011 |
| 8 | 5 | 0101 |
| 9 | 10 | 1010 |
| 10 | 7 | 0111 |
| 11 | 14 | 1110 |
| 12 | 15 | 1111 |
| 13 | 13 | 1101 |
| 14 | 9 | 1001 |
| 15 | 1 | 0001 |
Таким образом, при дальнейшем умножении весь цикл повторится снова. Полученные степени двойки не сложно умножать между собой, например: 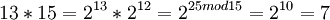 . Можно проверить результат,разделив
. Можно проверить результат,разделив 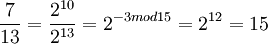 .
.
Таким образом, получили поле 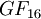 , то есть для двоичных 4-разрядных чисел.
, то есть для двоичных 4-разрядных чисел.
Коды Рида - Соломона
При построении кода Рида-Соломона задается пара чисел N,K, где N-Общее количество символов, а К- «полезное» количество символов, N-K символов задают избыточный код, предназначенный для восстановления ошибок.
Такой код Рида-Соломона будет иметь «расстояние Хемминга» 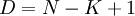 .
В соответствии с теорией кодирования, код, имеющий расстояние Хемминга
.
В соответствии с теорией кодирования, код, имеющий расстояние Хемминга 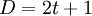 , позволяет восстанавливать t ошибок. Таким образом, если нам необходимо восстановить t ошибок, то общее количество символов сообщения
, позволяет восстанавливать t ошибок. Таким образом, если нам необходимо восстановить t ошибок, то общее количество символов сообщения 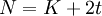 .
Сообщения при кодировании Рида-Соломона представляются полиномами.
Исходное сообщение представляется как коэффициенты полинома
.
Сообщения при кодировании Рида-Соломона представляются полиномами.
Исходное сообщение представляется как коэффициенты полинома 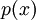 степени
степени 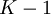 , имеющего
, имеющего 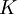 коэффициентов.
коэффициентов.
Порождающий многочлен Рида-Соломона,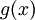 , строится следующий образом:
, строится следующий образом:
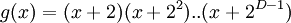 ,
, 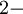 примитивный член поля. Нетрудно понять, что
примитивный член поля. Нетрудно понять, что 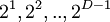 - корни этого многочлена.
- корни этого многочлена.
Например, построим порождающий многочлен кода Рида-Соломона с 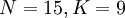 , способного исправлять до 3 ошибок
, способного исправлять до 3 ошибок 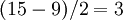 :
:
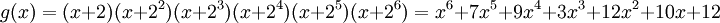 . (Возведение в степень и умножения выполнены над полем GF16 )!
. (Возведение в степень и умножения выполнены над полем GF16 )!
Кодирование Рида-Соломона
Кодирование Рида-Соломона будем производить систематическим кодом, это означает, что в закодированное сообщение будет содержать в себе в явном виде исходное сообщение. Каким образом это делается:
Сначала полином сдвигается на 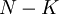 коэффициентов влево
коэффициентов влево
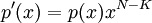 ,а потом вычисляется остаток от деления на порождающий полином и прибавляется к
,а потом вычисляется остаток от деления на порождающий полином и прибавляется к 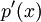 :
: 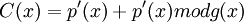 .
.
Для систематического кого очевидно, что 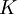 старших коэффициентов полученного кода
старших коэффициентов полученного кода 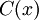 содержат исходное сообщение. Это удобно при декодировании.
Закодированное сообщение
содержат исходное сообщение. Это удобно при декодировании.
Закодированное сообщение 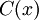 обладает очень важным свойством: оно без остатка делится на порождающий многочлен
обладает очень важным свойством: оно без остатка делится на порождающий многочлен 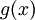 .
.
Докажем это свойство:
Пусь 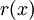 -остаток от деления
-остаток от деления 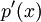 на
на 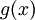 .
.
Тогда,
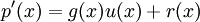
Итак,
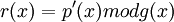
Тогда
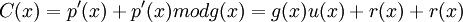
Вспомним, что в арифметике поля Галуа сложения являются одновременно и вычитанием, тогда 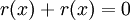 !Следовательно
!Следовательно 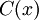 делится на
делится на 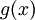 без остатка.
без остатка.
Таким образом,
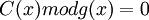
В случае, если закодированное сообщение будет изменено, то это равенство будет нарушенным, не считая случая, когда ошибка окажется кратной 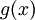 . Факт искажения можно рассматривать как прибавление к
. Факт искажения можно рассматривать как прибавление к 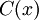 некоторого полинома ошибки
некоторого полинома ошибки 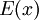 .
.
Пример:
Рассмотрим кодирование информации. Пусть наше сообщение такое:
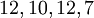
Полином сообщения получается такой:
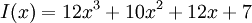
Умножаем на 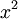 ,получаем:
,получаем:
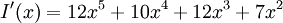
Делим на 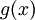 и получаем остаток:
и получаем остаток: 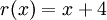
В итоге получается полином закодированного сообщения:
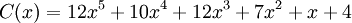
Декодирование Рида-Соломона
Первым шагом необходимо выполнить деление полинома на порождающий полином 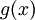 . Если остаток от деления равен 0, то сообщение не искажено и декодирование для систематического кода тривиально.
. Если остаток от деления равен 0, то сообщение не искажено и декодирование для систематического кода тривиально.
В случае же присутствия ошибки придется выполнить следующие действия:
Декодирование основано на построении многочлена синдрома ошибки S(x) и отыскании соответствующего ему многочлена локаторов L(x).
Локаторы ошибок – это элементы поля Галуа, степень которых совпадает с позицией ошибки. Так, если искажён коэффициент при 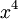 , то локатор этой ошибки равен
, то локатор этой ошибки равен 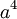 , если искажён коэффициент при
, если искажён коэффициент при 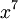 то локатор ошибки будет равен
то локатор ошибки будет равен 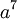 и т.п. (а – примитивный член, т.е. в нашем случае a=2).
Многочлен локаторов
и т.п. (а – примитивный член, т.е. в нашем случае a=2).
Многочлен локаторов 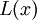 – это многочлен, корни которого обратны локаторам ошибок. Таким образом, многочлен
– это многочлен, корни которого обратны локаторам ошибок. Таким образом, многочлен 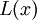 должен иметь вид
должен иметь вид
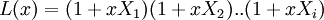
где 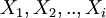 - локаторы ошибок
- локаторы ошибок
Ясно, что если этот многочлен будет найден, то мы легко сможем определить локаторы ошибок – для этого потребуется только определить его корни.
Для определения этого полинома сначала получают вспомогательный полином 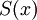 , так называемый синдром ошибки. Коэффициенты синдрома ошибки получаются подстановкой степеней примитивного члена в остаток многочлен
, так называемый синдром ошибки. Коэффициенты синдрома ошибки получаются подстановкой степеней примитивного члена в остаток многочлен 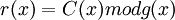 :
: 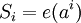
Между 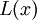 и
и 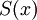 существует соотношение
существует соотношение
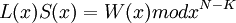
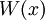 называется многочленом ошибок. Степень многочлена
называется многочленом ошибок. Степень многочлена 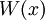 не может превышать
не может превышать 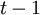 , где
, где 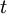 – количество ошибок, то есть в максимальном случае
– количество ошибок, то есть в максимальном случае 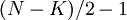
С учётом этого обстоятельства, а также учитывая, что свободный член 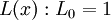 (ведь
(ведь 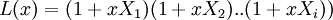 можно составить систему линейных уравнений.
можно составить систему линейных уравнений.
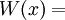
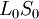
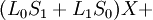
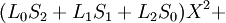
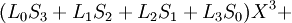
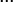
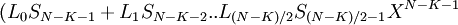
Пусть 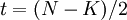
Коэффициенты при степенях от 0 до t – 1 не равны нулю, при старших степенях должны быть нулевыми.
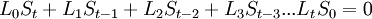
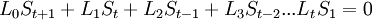
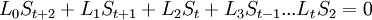
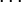
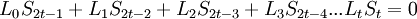
Коэффициент 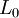 известен, остальные необходимо найти, следовательно требуется составить t уравнений.
известен, остальные необходимо найти, следовательно требуется составить t уравнений.
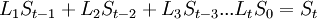
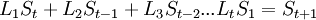
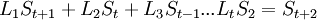
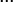
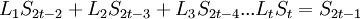
В матричном виде:
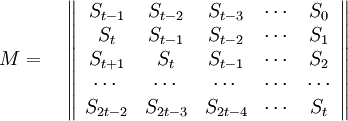
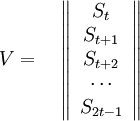
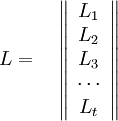
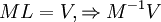 Например, для нашего примера – кода Рида-Соломона (6, 4) матрица M имеет вид:
Например, для нашего примера – кода Рида-Соломона (6, 4) матрица M имеет вид:
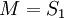 , а вектор
, а вектор 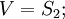
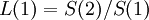
Таким образом, вычисление полинома локаторов сводится к построению матрицы M, нахождению обратной ей и умножению на вектор V.
Обратная матрица получается так же, как и в обычной математике, например Жордановым методом.
После того, как полином 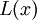 найден, следует найти его корни – они будут обратны к локаторам ошибок.
найден, следует найти его корни – они будут обратны к локаторам ошибок.
После нахождения позиции ошибки,займемся нахождением значением ошибки:
Воспользуемся определением синдромной функции:
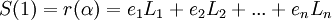 ,
,
где 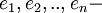 значение ошибки.
значение ошибки. 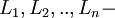 позиция ошибки.
позиция ошибки.
Для нашего кода