Китайская теорема об остатках — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 67: | Строка 67: | ||
Вычитая почленно из первого сравнения второе, получим истинное сравнение <math>(x-x') \equiv 0 \pmod{p_i}</math>, | Вычитая почленно из первого сравнения второе, получим истинное сравнение <math>(x-x') \equiv 0 \pmod{p_i}</math>, | ||
| − | откуда следует, что | + | откуда следует, что для всех <math>i=1,\ldots,k</math> <math>(x-x')</math> делится нацело на <math>p_i</math>. Но тогда <math>(x-x')</math> делится нацело на <math>p</math>,следовательно, <math>x=x</math>, так как <math>|x-x'|<p</math>. |
| + | |||
| + | Теорема доказана. | ||
Версия 14:23, 2 сентября 2014
Китайская теорема об остатках формулируется следующим образом:
Теорема.
Пусть 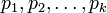 - попарно взаимно простые числа, большие 1, и пусть
- попарно взаимно простые числа, большие 1, и пусть 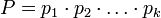 . Тогда существует единственное неотрицательное решение по модулю
. Тогда существует единственное неотрицательное решение по модулю 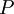 следующей системы сравнений:
следующей системы сравнений:
-
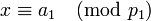 ,
,
-
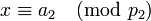 ,
,
-
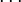 ,
,
-
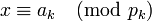 .
.
Другими словами, отображение, которое каждому целому числу  ,
, 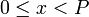 , ставит в соответствие кортеж
, ставит в соответствие кортеж 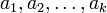 , где
, где 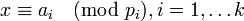 является биекцией кольца
является биекцией кольца 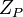 на декартово произведение
на декартово произведение 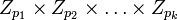 колец
колец 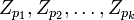 .
.
Т.е. соответствие между числами и кортежами является взаимно однозначным, кроме того, операции, выполняемые над числом  , можно эквивалентно выполнять над соответствующими элементами кортежами путём независимого выполнения операций над каждым компонентом:
, можно эквивалентно выполнять над соответствующими элементами кортежами путём независимого выполнения операций над каждым компонентом:
если
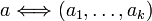 ,
,
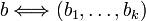 ,
,
то справедливо:
-
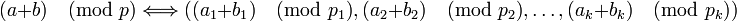 ,
,
-
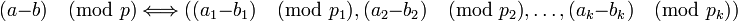 ,
,
-
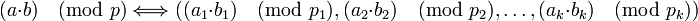 .
.
Существует много различных доказательств китайской теоремы об остатках. Приведём конструктивное доказательство этой теоремы.
Доказательство.
Найдём число 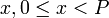 , удовлетворяющее одновременно всем сравнениям, указанным в теореме. Систему сравнений будем решать присоединением на каждом шаге нового сравнения. Первое сравнение справедливо для всякого целого числа
, удовлетворяющее одновременно всем сравнениям, указанным в теореме. Систему сравнений будем решать присоединением на каждом шаге нового сравнения. Первое сравнение справедливо для всякого целого числа  вида
вида
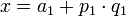 , где
, где 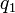 - произвольное целое число.
- произвольное целое число.
Для нахождения 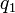 подставим значение
подставим значение  во второе сравнение системы,
после чего получим
во второе сравнение системы,
после чего получим 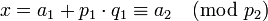 ,
откуда
,
откуда 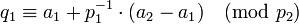 ,
,
где 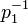 - обратный мультипликативный элемент к
- обратный мультипликативный элемент к 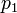 по модулю
по модулю 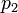 .
Такой элемент существует, так как
.
Такой элемент существует, так как 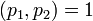 .
.
Найденное таким образом 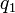 можно записать в виде
можно записать в виде
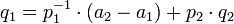
для некоторого целого числа 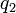 .
.
Подставим значение 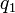 в выражение
в выражение
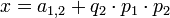 .
.
Теперь первые два сравнения могут быть заменены на одно
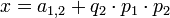 .
.
Применим теперь описанную процедуру к полученному сравнению и к одному из оставшихся сравнений исходной системы. Повторяя этот процесс 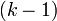 раз, мы в конечном итоге найдём число
раз, мы в конечном итоге найдём число  , удовлетворяющее всем сравнениям исходной системы.
Докажем единственность решения. Воспользуемся методом от противного. Предположим, что существует другое решение
, удовлетворяющее всем сравнениям исходной системы.
Докажем единственность решения. Воспользуемся методом от противного. Предположим, что существует другое решение 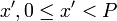 исходной системы.
исходной системы.
Тогда
для всех 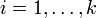 .
.
Вычитая почленно из первого сравнения второе, получим истинное сравнение 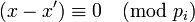 ,
откуда следует, что для всех
,
откуда следует, что для всех 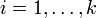
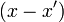 делится нацело на
делится нацело на 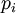 . Но тогда
. Но тогда 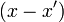 делится нацело на
делится нацело на  ,следовательно,
,следовательно,  , так как
, так как  .
.
Теорема доказана.