Система остаточных классов — различия между версиями
Turbo (обсуждение | вклад) |
Turbo (обсуждение | вклад) |
||
| Строка 6: | Строка 6: | ||
При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка <math>[0,M-1]</math>. | При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка <math>[0,M-1]</math>. | ||
| − | == Преимущества | + | == Преимущества системы остаточных классов == |
| − | В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в <math>[0,M-1]</math>. | + | * В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в <math>[0,M-1]</math>. |
| − | == Недостатки | + | == Недостатки системы остаточных классов == |
| − | + | * Возможность представления только ограниченного количества чисел. | |
| + | * Отсутствие эффективных алгоритмов для сравнения чисел, представленных в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям <math>(m_1, m_1\cdot m_2, \dots, m_1\cdot m_2\cdot\dots\cdot m_{n-1})</math>. | ||
| + | * Сложные реализации алгоритмов перевода из позиционной системы счисления в СОК и обратно. | ||
| + | |||
| + | == Применение системы остаточных классов == | ||
| + | СОК широко используется в микроэлектронике в специализированных устройствах [ЦОС], где требуется: | ||
| + | * контроль за ошибками, за счет введения дополнительных избыточных модулей | ||
| + | * высокая скорость работы, которую обеспечивает параллельная реализация базовых операций | ||
== Основные определения == | == Основные определения == | ||
Версия 13:02, 30 января 2013
Система остаточных классов (СОК) (от англ. Residue number system, другое название Модулярная арифметика) - непозиционная система счисления. Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором взаимно простых модулей 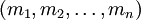 с произведением
с произведением 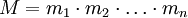 так, что каждому целому числу
так, что каждому целому числу  из отрезка
из отрезка ![[0,M-1]](/w/images/math/5/6/5/56591240ff770cb9db7f3205c6befa98.png) ставится в соответствие набор вычетов
ставится в соответствие набор вычетов 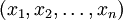 , где
, где
-
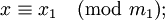
-
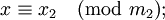
- …
-
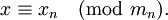
При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка ![[0,M-1]](/w/images/math/5/6/5/56591240ff770cb9db7f3205c6befa98.png) .
.
Содержание
Преимущества системы остаточных классов
- В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в
![[0,M-1]](/w/images/math/5/6/5/56591240ff770cb9db7f3205c6befa98.png) .
.
Недостатки системы остаточных классов
- Возможность представления только ограниченного количества чисел.
- Отсутствие эффективных алгоритмов для сравнения чисел, представленных в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям
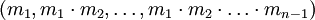 .
.
- Сложные реализации алгоритмов перевода из позиционной системы счисления в СОК и обратно.
Применение системы остаточных классов
СОК широко используется в микроэлектронике в специализированных устройствах [ЦОС], где требуется:
- контроль за ошибками, за счет введения дополнительных избыточных модулей
- высокая скорость работы, которую обеспечивает параллельная реализация базовых операций
Основные определения
Система остаточных классов используется для представления больших чисел 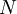 , обеспечивая таким образом более эффективные вычисления. В основе данного представления лежит изоморфизм
, обеспечивая таким образом более эффективные вычисления. В основе данного представления лежит изоморфизм 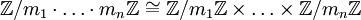 , который доставляет китайская теорема об остатках.
, который доставляет китайская теорема об остатках.
Системой остаточных классов называют произвольное конечное множество 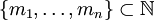 , такое что
, такое что 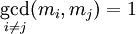 , где
, где 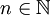 . Пусть задана произвольная система остаточных классов
. Пусть задана произвольная система остаточных классов 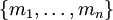 и положим, что
и положим, что 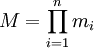 . Тогда в силу китайской теоремы об остатках имеем эпиморфизм колец
. Тогда в силу китайской теоремы об остатках имеем эпиморфизм колец 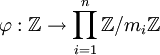 , т.ч.
, т.ч. 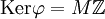 , который индуцирует канонический изоморфизм
, который индуцирует канонический изоморфизм 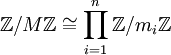 .
.
Выполнение арифметических операций
С использованием системы остаточных классов можно выполнять основные арифметические операции.
Сложение и вычитание
Пусть 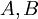 - произвольные натуральные числа. Положим, что
- произвольные натуральные числа. Положим, что 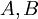 представляются в виде системы остаточных классов как
представляются в виде системы остаточных классов как 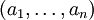 и
и 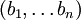 соответственно. Формально,
соответственно. Формально, 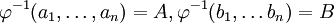 . В силу того, что
. В силу того, что 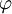 - изоморфизм будем иметь
- изоморфизм будем иметь 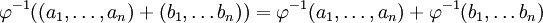 . Обозначим через
. Обозначим через 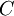 остаток
остаток 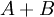 от деления на
от деления на 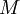 . Тогда
. Тогда 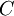 представляется в виде системы остаточных классов как
представляется в виде системы остаточных классов как 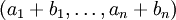 .
.
Умножение
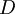 - остаток от деления
- остаток от деления 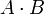 на
на 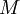 . Тогда
. Тогда 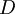 представляется в виде системы остаточных классов как
представляется в виде системы остаточных классов как 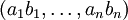 .
.
Деление
Деление  на
на 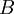 с использованием системы остаточных классов можно выполнять не всегда. Положим, что
с использованием системы остаточных классов можно выполнять не всегда. Положим, что 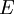 - остаток
- остаток 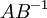 от деления на
от деления на 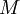 . На языке теории колец это означает, что
. На языке теории колец это означает, что 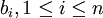 обратим и
обратим и 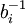 - обратный. Тогда
- обратный. Тогда 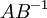 представляется в виде
представляется в виде 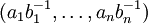 .
.
Факторизация полупростых чисел
Пусть 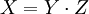 - полупростое число. Рассмотрим систему остаточных классов
- полупростое число. Рассмотрим систему остаточных классов 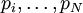 , где
, где 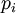 —
— 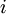 -е простое число.
-е простое число.