Интервальные методы перевода — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 28: | Строка 28: | ||
:<math>A = \left| \sum _{i = 1}^{n} {P_i}^{\phi(p_i)} \cdot \alpha_i \right| \pmod P</math> (4). | :<math>A = \left| \sum _{i = 1}^{n} {P_i}^{\phi(p_i)} \cdot \alpha_i \right| \pmod P</math> (4). | ||
| − | Для определения номера интервала <math>l_A<math>, подставим выражение (4) в (1): | + | Для определения номера интервала <math>l_A</math>, подставим выражение (4) в (1): |
:<math>l_A = \left [\frac {A}{p_i}\right ]</math> | :<math>l_A = \left [\frac {A}{p_i}\right ]</math> | ||
Версия 09:33, 12 ноября 2014
Достаточно эффективными методами перевода чисел из СОК в ПСС являются интервальные методы, основанные на интервальных характеристиках чисел. Одна из таких характеристик – номер интервала.
Рассмотрим СОК, заданную системой оснований 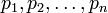 с объёмом диапазона
с объёмом диапазона 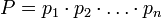 . Выберем дробящий модуль
. Выберем дробящий модуль 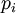 и проведём дробление заданного диапазона на интервалы путём деления
и проведём дробление заданного диапазона на интервалы путём деления 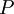 на модуль
на модуль 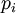 . Тогда количество интервалов
. Тогда количество интервалов 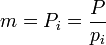 , а длина интервала определяется величиной модуля.
, а длина интервала определяется величиной модуля.
В результате величину любого числа  , заданного в СОК по выбранным основаниям, можно определить по номеру интервала:
, заданного в СОК по выбранным основаниям, можно определить по номеру интервала:
![l_A = \left [\frac {A}{p_i}\right ]](/w/images/math/7/5/9/75929eadc0f79d2461ea15f97e144892.png) (1),
(1),
в котором находится число  , и по цифре
, и по цифре 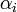 числа
числа  в СОК по модулю
в СОК по модулю 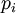 , т.е.
, т.е.
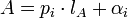 (2).
(2).
Так как 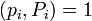 , то по теореме Эйлера:
, то по теореме Эйлера:
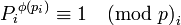 (3),
(3),
где 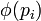 - – функция Эйлера.
Причём если
- – функция Эйлера.
Причём если 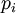 – простое число, то
– простое число, то 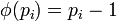 .
.
Число  можно представить в виде
можно представить в виде
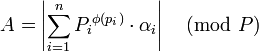 (4).
(4).
Для определения номера интервала 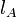 , подставим выражение (4) в (1):
, подставим выражение (4) в (1):