Расширение диапазона представления чисел — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 2: | Строка 2: | ||
Задачу расширения системы оснований можно сформулировать следующим образом: найти остаточное представление числа по новому основанию (новым основаниям), если известно представление числа по другим основаниям остатки от деления на другие числа. | Задачу расширения системы оснований можно сформулировать следующим образом: найти остаточное представление числа по новому основанию (новым основаниям), если известно представление числа по другим основаниям остатки от деления на другие числа. | ||
Один из путей расширения системы оснований состоит в переводе числа в позиционную систему счисления и вычисления остатка от деления на новый модуль. Этот путь не является рациональным с точки зрения числа операций. | Один из путей расширения системы оснований состоит в переводе числа в позиционную систему счисления и вычисления остатка от деления на новый модуль. Этот путь не является рациональным с точки зрения числа операций. | ||
| − | Другой метод расширения системы оснований позволяет определить цифру числа по новому основанию, базируясь на таких позиционных характеристиках числа, как ранг числа, след числа. Пусть вновь задана система оснований <math>p_1, p_2, \ldots, p_n</math> с диапазоном <math>P</math>, ортогональными базисами <math>B_1, B_2, \ldots, B_n</math>, веса которых <math>m_1, m_2, \ldots, m_n</math>. По определению, <math>B_i = m_i \cdot \frac{P}{p_i}, i=1, \ldots, n</math>. Пусть в этой системе задано число <math>A = ({\alpha}_1, {\alpha}_2, \ldots, {\alpha}_n)</math>. Расширим систему оснований, добавляя основание <math>p_{n+1}</math>, тогда диапазон системы станет <math>P' = p_{n+1} \cdot P</math>, ортогональные базисы системы <math>{B_1}', {B_2}', \ldots, {B_n}', {B_{n+1}}'</math>, их веса <math>{m_1}', {m_2}', \ldots, {m_n}', {m_{n+1}}'</math>, причём <math>{B_i}' = {m_i} \cdot \frac{p_{n+1} \cdot P}{p_i}, i=1, \ldots, n+1</math>. Задача состоит в определении цифры <math>{\alpha}_{n+1})</math> числа <math>A = ({\alpha}_1, {\alpha}_2, \ldots, {\alpha}_n)</math> по основанию <math>p_{n+1}</math>. Минимальным следом числа называют цифру <math>{S*}_A</math>, при которой число <math>A* = ({\alpha}_1, {\alpha}_2, \ldots, {\alpha}_n), {S*}_A</math> находится в интервале <math> \left[0,\frac{P'}{p_{n+1}}\right]</math>, и число <math>A \in \left[0,P\right)</math>. Определение цифры по основанию <math>p_{n+1}</math> сводится тогда к определению минимального следа числа <math>A</math> в расширенной системе оснований. | + | Другой метод расширения системы оснований позволяет определить цифру числа по новому основанию, базируясь на таких позиционных характеристиках числа, как ранг числа, след числа. Пусть вновь задана система оснований <math>p_1, p_2, \ldots, p_n</math> с диапазоном <math>P</math>, ортогональными базисами <math>B_1, B_2, \ldots, B_n</math>, веса которых <math>m_1, m_2, \ldots, m_n</math>. По определению, <math>B_i = m_i \cdot \frac{P}{p_i}, i=1, \ldots, n</math>. Пусть в этой системе задано число <math>A = ({\alpha}_1, {\alpha}_2, \ldots, {\alpha}_n)</math>. Расширим систему оснований, добавляя основание <math>p_{n+1}</math>, тогда диапазон системы станет <math>P' = p_{n+1} \cdot P</math>, ортогональные базисы системы <math>{B_1}', {B_2}', \ldots, {B_n}', {B_{n+1}}'</math>, их веса <math>{m_1}', {m_2}', \ldots, {m_n}', {m_{n+1}}'</math>, причём <math>{B_i}' = {m_i} \cdot \frac{p_{n+1} \cdot P}{p_i}, i=1, \ldots, n+1</math>. Задача состоит в определении цифры <math>{\alpha}_{n+1})</math> числа <math>A = ({\alpha}_1, {\alpha}_2, \ldots, {\alpha}_n)</math> по основанию <math>p_{n+1}</math>. Минимальным следом числа называют цифру <math>{S^*}_A</math>, при которой число <math>A^* = ({\alpha}_1, {\alpha}_2, \ldots, {\alpha}_n), {S^*}_A</math> находится в интервале <math> \left[0,\frac{P'}{p_{n+1}}\right]</math>, и число <math>A \in \left[0,P\right)</math>. Определение цифры по основанию <math>p_{n+1}</math> сводится тогда к определению минимального следа числа <math>A</math> в расширенной системе оснований. |
Текущая версия на 14:39, 3 декабря 2014
Расширение системы оснований является одной из основных немодульных операций в СОК. Выполнение этой операции бывает необходимо при выполнении операции деления чисел, при вычислении позиционных характеристик, при обнаружении переполнения при выполнении сложения или умножения чисел.
Задачу расширения системы оснований можно сформулировать следующим образом: найти остаточное представление числа по новому основанию (новым основаниям), если известно представление числа по другим основаниям остатки от деления на другие числа.
Один из путей расширения системы оснований состоит в переводе числа в позиционную систему счисления и вычисления остатка от деления на новый модуль. Этот путь не является рациональным с точки зрения числа операций.
Другой метод расширения системы оснований позволяет определить цифру числа по новому основанию, базируясь на таких позиционных характеристиках числа, как ранг числа, след числа. Пусть вновь задана система оснований 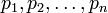 с диапазоном
с диапазоном 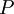 , ортогональными базисами
, ортогональными базисами 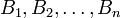 , веса которых
, веса которых 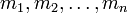 . По определению,
. По определению, 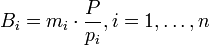 . Пусть в этой системе задано число
. Пусть в этой системе задано число 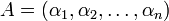 . Расширим систему оснований, добавляя основание
. Расширим систему оснований, добавляя основание 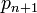 , тогда диапазон системы станет
, тогда диапазон системы станет 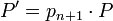 , ортогональные базисы системы
, ортогональные базисы системы 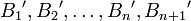 , их веса
, их веса 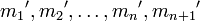 , причём
, причём 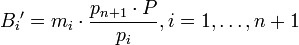 . Задача состоит в определении цифры
. Задача состоит в определении цифры 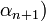 числа
числа 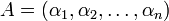 по основанию
по основанию 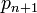 . Минимальным следом числа называют цифру
. Минимальным следом числа называют цифру 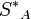 , при которой число
, при которой число 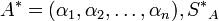 находится в интервале
находится в интервале ![\left[0,\frac{P'}{p_{n+1}}\right]](/w/images/math/d/0/7/d079edb5898fc3c179b9df39e74763cd.png) , и число
, и число 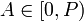 . Определение цифры по основанию
. Определение цифры по основанию 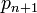 сводится тогда к определению минимального следа числа
сводится тогда к определению минимального следа числа  в расширенной системе оснований.
в расширенной системе оснований.