Теорема о делении с остатком. Алгоритм Евклида — различия между версиями
Материал из Модулярная арифметики
Isaeva (обсуждение | вклад) (Новая страница: «'''Пример'''») |
Isaeva (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
'''Пример''' | '''Пример''' | ||
| + | |||
| + | Пусть модуль <math>p = 6</math>. | ||
| + | |||
| + | Тогда имеем шесть классов разбиения множества целых чисел по модулю 6: | ||
| + | |||
| + | :<math>K_0 = {\ldots,-18,-12,-6,0,6,12,18,\ldots}, r=0</math>; | ||
| + | |||
| + | :<math>K_1 = {\ldots,-17,-11,-5,1,7,13,19,\ldots}, r=1</math>; | ||
| + | |||
| + | :<math>K_2 = {\ldots,-16,-10,-4,2,8,14,20,\ldots}, r=2</math>; | ||
| + | |||
| + | :<math>K_3 = {\ldots,-15,-9,-3,3,9,15,21,\ldots}, r=3</math>; | ||
| + | |||
| + | :<math>K_4 = {\ldots,-14,-8,-2,4,10,16,22,\ldots}, r=4</math>; | ||
| + | |||
| + | :<math>K_5 = {\ldots,-13,-7,-1,5,11,17,23,\ldots}, r=5</math>, | ||
| + | |||
| + | где через <math>r</math> обозначен остаток от деления целого числа на 6. | ||
Версия 12:44, 10 декабря 2014
Пример
Пусть модуль 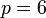 .
.
Тогда имеем шесть классов разбиения множества целых чисел по модулю 6:
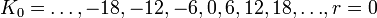 ;
;
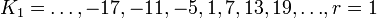 ;
;
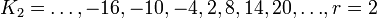 ;
;
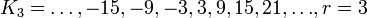 ;
;
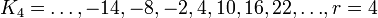 ;
;
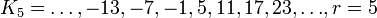 ,
,
где через  обозначен остаток от деления целого числа на 6.
обозначен остаток от деления целого числа на 6.