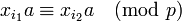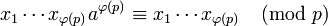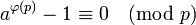Вычисление мультипликативных обратных элементов по заданному модулю — различия между версиями
Isaeva (обсуждение | вклад) |
Isaeva (обсуждение | вклад) |
||
| Строка 12: | Строка 12: | ||
'''Определение''' | '''Определение''' | ||
| − | Функция Эйлера <math> | + | Функция Эйлера <math>\varphi (n)</math> — это количество чисел от <math>1</math> до <math>n</math>, взаимно простых с <math>n</math>. |
| Строка 20: | Строка 20: | ||
'''Tеоремa Эйлера''' | '''Tеоремa Эйлера''' | ||
| − | Если <math>a</math> и <math>p</math> взаимно просты, то <math>a^{ | + | Если <math>a</math> и <math>p</math> взаимно просты, то <math>a^{\varphi(p)} \equiv 1 \pmod p</math>, где <math>\varphi (n)</math> - функция Эйлера. |
| Строка 27: | Строка 27: | ||
Доказательство. | Доказательство. | ||
| − | Пусть <math>x_1, \dots, x_{ | + | Пусть <math>x_1, \dots, x_{\varphi(p)}</math> — все различные натуральные числа, меньшие <math>p</math> и взаимно простые с ним. |
Рассмотрим все возможные произведения <math>x_i a</math> для всех <math>i</math> от <math>1</math> до <math>\varphi(p)</math>. | Рассмотрим все возможные произведения <math>x_i a</math> для всех <math>i</math> от <math>1</math> до <math>\varphi(p)</math>. | ||
| Строка 40: | Строка 40: | ||
Так как <math>a</math> взаимно просто с <math>p</math>, то последнее равенство равносильно тому, что | Так как <math>a</math> взаимно просто с <math>p</math>, то последнее равенство равносильно тому, что | ||
: <math>x_{i_1} - x_{i_2} \equiv 0\pmod p</math> или <math>x_{i_1} \equiv x_{i_2}\pmod p</math>. | : <math>x_{i_1} - x_{i_2} \equiv 0\pmod p</math> или <math>x_{i_1} \equiv x_{i_2}\pmod p</math>. | ||
| − | Это противоречит тому, что числа <math>x_1, \dots, x_{ | + | Это противоречит тому, что числа <math>x_1, \dots, x_{\varphi(p)}</math> попарно различны по модулю <math>p</math>. |
Перемножим все сравнения вида <math>x_i a \equiv x_j\pmod p</math>. Получим: | Перемножим все сравнения вида <math>x_i a \equiv x_j\pmod p</math>. Получим: | ||
| − | : <math>x_1 \cdots x_{ | + | : <math>x_1 \cdots x_{\varphi(p)} a^{\varphi(p)} \equiv x_1 \cdots x_{\varphi(p)}\pmod p</math> |
или | или | ||
| − | : <math>x_1 \cdots x_{ | + | : <math>x_1 \cdots x_{\varphi(p)} (a^{\varphi(p)}-1) \equiv 0\pmod p</math>. |
| − | Так как число <math>x_1 \cdots x_{ | + | Так как число <math>x_1 \cdots x_{\varphi(p)}</math> взаимно просто с <math>p</math>, то последнее сравнение равносильно тому, что |
| − | : <math>a^{ | + | : <math>a^{\varphi(p)}-1 \equiv 0\pmod p</math> |
или | или | ||
| − | :<math>a^{ | + | :<math>a^{\varphi(p)} \equiv 1\pmod p</math>. |
Версия 12:56, 23 января 2015
Рассмотрим вопрос о мультипликативных обратных элементов по заданному модулю в фактор-кольце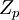 
.
Рассмотрим два способа вычисления обратных мультипликативных элементов. Первый способ основан на рассмотренном выше алгоритме Евклида, второй – на теореме Эйлера.
Первый способ
Второй способ
Напомним теорему Эйлера.
Определение
Функция Эйлера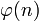 
— это количество чисел от 
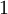до 
, взаимно простых с .
Т.е. это количество таких натуральных чисел из отрезка [1; n], наибольший общий делитель (НОД) которых с равен единице.
Tеоремa Эйлера
Если 
и 
взаимно просты, то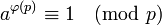 
, где 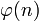- функция Эйлера.
Доказательство теоремы достаточно простое, возможны различные варианты. Приведем здесь теоретико-числовое доказательство.
Доказательство.
Пусть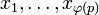 
— все различные натуральные числа, меньшие и взаимно простые с ним.
Рассмотрим все возможные произведения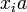 
для всех 
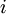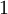от до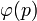 
.
Поскольку взаимно просто с и 
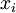взаимно просто с , то и 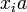также взаимно просто с , то есть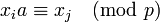 
для некоторого 
.
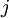Отметим, что все остатки 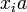при делении на различны. Действительно, пусть это не так, то существуют такие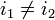 
, что
или
-
.
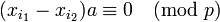Так как взаимно просто с , то последнее равенство равносильно тому, что
-
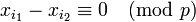или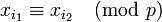 
.
Это противоречит тому, что числа 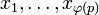попарно различны по модулю .
Перемножим все сравнения вида 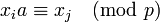. Получим:
или
-
.
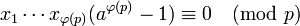Так как число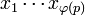 
взаимно просто с , то последнее сравнение равносильно тому, что
или
- .
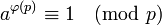В частном случае, когда простое, теорема Эйлера превращается в так называемую малую теорему Ферма:
Малая теорема Ферма
Если - простое число и - произвольное целое число, не делящееся на , то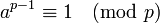 
.
