Аппаратные реализации модулярных сумматоров и умножителей на базе минимизированной таблицы истинности — различия между версиями

Материал из Модулярная арифметики
Перейти к: навигация, поиск
(Новая страница: «В данной статье приведен метод реализации модулярных сумматоров и умножителей на базе т…»)
 
Строка 3: Строка 3:
 
== Описание ==
 
== Описание ==
  
−
Модулярные сумматоры и умножители в силу своей малой размерности могут быть реализованы как произвольная логическая функция и описана в виде таблицы истинности.  
+
Модулярные сумматоры и умножители в силу своей малой размерности могут быть реализованы как произвольная логическая функция и описана в виде таблицы истинности. Если размерность модуля <math>p</math> равна <math>k</math> бит, то таблица истинности будет иметь <math>2k</math> входных столбцов и <math>2^{2k}</math> строк. Для выходов будет соответственно <math>k</math> столбцов. Так как в модулярных устройствах размерность модуля небольшая, то и размерность таблицы истинности обычно приемлемых размеров. Получив таблицу истинности её можно минимизировать и записать для каждого выхода выражение как ДНФ.  
  
 
== Пример Verilog файла ==
 
== Пример Verilog файла ==
 +
 +
* Пример для умножителя по модулю 5.
 +
 +
<pre>
 +
module mul_modulo_5 (A, B, X);
 +
    input [2:0] A;
 +
    input [2:0] B;
 +
    output[2:0] X;
 +
 +
    assign X[0] = (A[0]&B[0]&~B[1]) | (~A[0]&A[1]&B[0]&B[1]) | (A[0]&~A[1]&B[0]) | (A[0]&A[1]&~B[0]&B[1]) | (A[2]&B[2]) | (A[2]&~B[0]&B[1]) | (~A[0]&A[1]&B[2]);
 +
    assign X[1] = (A[0]&~A[1]&B[1]) | (A[1]&B[0]&~B[1]) | (A[1]&B[2]) | (A[2]&B[1]);
 +
    assign X[2] = (A[0]&~A[1]&B[2]) | (~A[0]&A[1]&~B[0]&B[1]) | (A[0]&A[1]&B[0]&B[1]) | (A[2]&B[0]&~B[1]);
 +
endmodule
 +
</pre>
  
 
== Ссылки на файлы ==
 
== Ссылки на файлы ==
 +
 +
Модулярные сумматоры и умножители были синтезированы для всех модулей от 2 до 255 включительно. Скачать Verilog файлы можно ниже:
 +
* [Модулярные сумматоры (.7z ~3MB)|http://vscripts.ru/res/2015/sum_mod3-255_espr.7z]
 +
* [Модулярные умножители (.7z ~40MB)|http://vscripts.ru/res/2015/mul_mod3-255_espr.7z]

Версия 11:49, 21 декабря 2015

В данной статье приведен метод реализации модулярных сумматоров и умножителей на базе таблиц истинности, минимизированных с помощью Espresso.

Описание

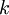Модулярные сумматоры и умножители в силу своей малой размерности могут быть реализованы как произвольная логическая функция и описана в виде таблицы истинности. Если размерность модуля p равна k бит, то таблица истинности будет иметь 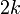2k входных столбцов и 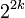2^{2k} строк. Для выходов будет соответственно 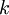k столбцов. Так как в модулярных устройствах размерность модуля небольшая, то и размерность таблицы истинности обычно приемлемых размеров. Получив таблицу истинности её можно минимизировать и записать для каждого выхода выражение как ДНФ.

Пример Verilog файла

  • Пример для умножителя по модулю 5. 
module mul_modulo_5 (A, B, X);
    input [2:0] A;
    input [2:0] B;
    output[2:0] X;

    assign X[0] = (A[0]&B[0]&~B[1]) | (~A[0]&A[1]&B[0]&B[1]) | (A[0]&~A[1]&B[0]) | (A[0]&A[1]&~B[0]&B[1]) | (A[2]&B[2]) | (A[2]&~B[0]&B[1]) | (~A[0]&A[1]&B[2]);
    assign X[1] = (A[0]&~A[1]&B[1]) | (A[1]&B[0]&~B[1]) | (A[1]&B[2]) | (A[2]&B[1]);
    assign X[2] = (A[0]&~A[1]&B[2]) | (~A[0]&A[1]&~B[0]&B[1]) | (A[0]&A[1]&B[0]&B[1]) | (A[2]&B[0]&~B[1]);
endmodule

Ссылки на файлы

Модулярные сумматоры и умножители были синтезированы для всех модулей от 2 до 255 включительно. Скачать Verilog файлы можно ниже:

Источник — «https://vscripts.ru/w/index.php?title=Аппаратные_реализации_модулярных_сумматоров_и_умножителей_на_базе_минимизированной_таблицы_истинности&oldid=1125»