Результат сравнения различных методов построения модулярных умножителей (индексный метод, разность квадратов, метод Espresso) — различия между версиями
Turbo (обсуждение | вклад) |
Turbo (обсуждение | вклад) |
||
| Строка 9: | Строка 9: | ||
| − | 1. Индексный модулярный умножитель (на примере модуля 7) | + | 1. Индексный модулярный умножитель (на примере модуля 7) |
| − | <pre | + | <pre class="mw-collapsible mw-collapsed"> |
module multiplication_mod_7(inp1, inp2, out); | module multiplication_mod_7(inp1, inp2, out); | ||
input [2:0] inp1; | input [2:0] inp1; | ||
| Строка 197: | Строка 197: | ||
2. Модулярный умножитель на базе формулы разности квадратов (на примере модуля 7) | 2. Модулярный умножитель на базе формулы разности квадратов (на примере модуля 7) | ||
| − | <pre> | + | <pre class="mw-collapsible mw-collapsed"> |
module multiplication_mod_7(inp1, inp2, out); | module multiplication_mod_7(inp1, inp2, out); | ||
input [2:0] inp1; | input [2:0] inp1; | ||
| Строка 331: | Строка 331: | ||
2. Модулярный сумматор по методу Espresso (на примере модуля 10) | 2. Модулярный сумматор по методу Espresso (на примере модуля 10) | ||
| − | <pre> | + | <pre class="mw-collapsible mw-collapsed"> |
module mul_mod10 (out, a, b); | module mul_mod10 (out, a, b); | ||
Текущая версия на 09:15, 27 мая 2013
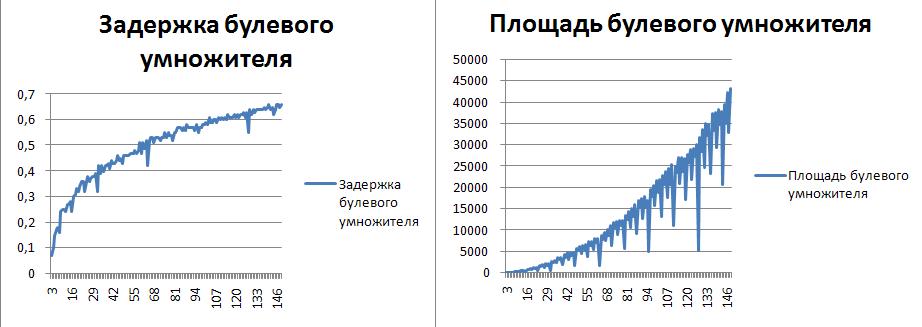
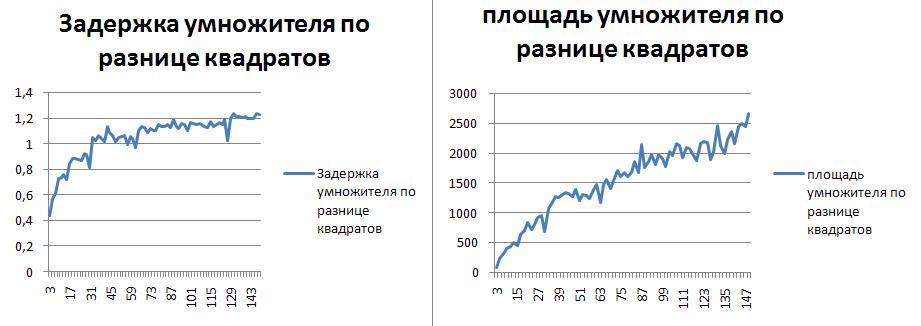
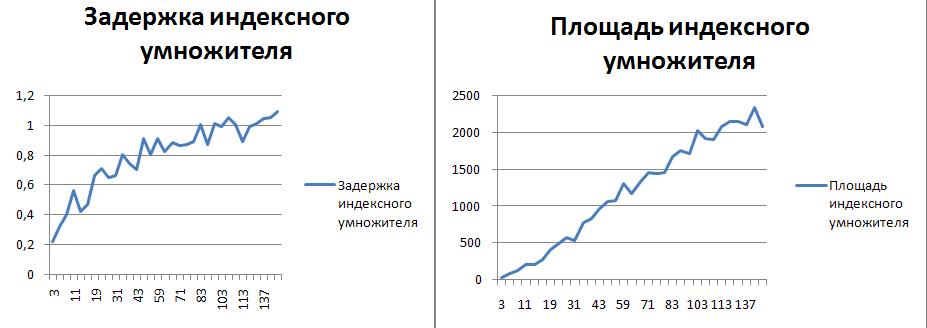
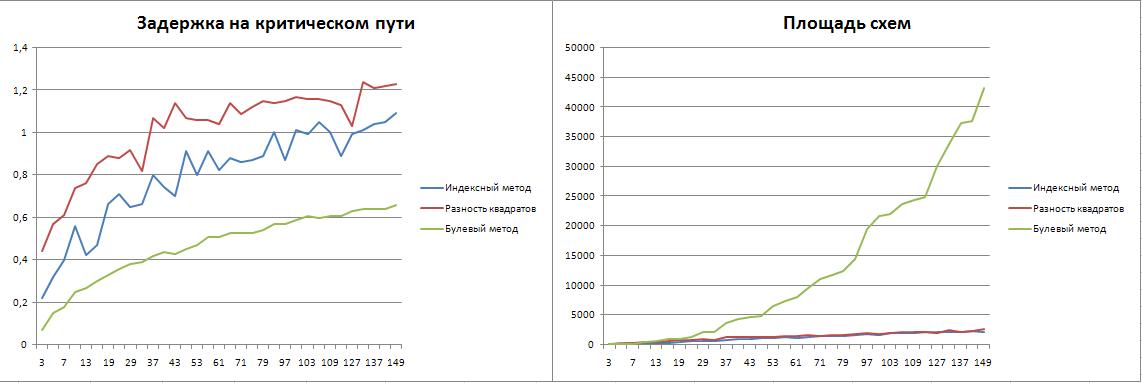
Было проведено сравнение модулярных умножителей. Рассматриваемые методы:
- Метод минимизации логических функций на базе алгоритма Espresso
- Метод разности квадратов
- Индексная реализация умножителя
Метод Espresso заключается в построении таблицы истинности для операции модулярного умножения, и дальнейшей минимизации получившейся булевой функции методом Espresso. Сравнение проводилось для расширенного набора оснований в диапазоне 3-149. Индексный метод работает только для простых чисел, метод, основанный на разности квадратов допускает любые нечетные числа, а метод Espresso работает для любых целых чисел. Маршрут проектирования для схем Espresso включал минимизацию булевых функций с помощью программного средства Logic Friday. Для автоматизации запуска Logic Friday использовался язык автоматизации AutoIt. Для остальных двух схем использовался стандартный подход с реализацией автоматизироанных генераторов.
Содержание
Типовые Verilog-модули
1. Индексный модулярный умножитель (на примере модуля 7)
module multiplication_mod_7(inp1, inp2, out);
input [2:0] inp1;
input [2:0] inp2;
output reg [2:0] out;
wire [2:0] out_pre;
wire [1:0] w_1_0;
wire [1:0] w_2_0;
wire [1:0] wout_0;
wire [1:0] w_1_1;
wire [1:0] w_2_1;
wire [1:0] wout_1;
lut_input_7 lut1(inp1, w_1_0, w_1_1);
lut_input_7 lut2(inp2, w_2_0, w_2_1);
sum_modulo_2 sm0(w_1_0, w_2_0, wout_0);
sum_modulo_3 sm1(w_1_1, w_2_1, wout_1);
lut_output_7 lut3(wout_0, wout_1, out_pre);
always @ (*)
begin
if (inp1 == 0 || inp2 == 0)
begin
out = 0;
end
else
begin
out = out_pre;
end
end
endmodule
module sum_modulo_2(inp1, inp2, out);
input [1:0] inp1;
input [1:0] inp2;
output reg [1:0] out;
wire [2:0] int;
assign int = inp1 + inp2;
always @ (*)
begin
if (int < 2)
begin
out = int;
end
else
begin
out = int - 2;
end
end
endmodule
module sum_modulo_3(inp1, inp2, out);
input [1:0] inp1;
input [1:0] inp2;
output reg [1:0] out;
wire [2:0] int;
assign int = inp1 + inp2;
always @ (*)
begin
if (int < 3)
begin
out = int;
end
else
begin
out = int - 3;
end
end
endmodule
module lut_output_7(inp0, inp1, out);
output reg [2:0] out;
input [1:0] inp0;
input [1:0] inp1;
always @ (*)
begin
if (inp0 == 0 && inp1 == 0)
begin
out <= 1;
end
else if (inp0 == 0 && inp1 == 2)
begin
out <= 2;
end
else if (inp0 == 1 && inp1 == 1)
begin
out <= 3;
end
else if (inp0 == 0 && inp1 == 1)
begin
out <= 4;
end
else if (inp0 == 1 && inp1 == 2)
begin
out <= 5;
end
else if (inp0 == 1 && inp1 == 0)
begin
out <= 6;
end
else
begin
out <= 0;
end
end
endmodule
module lut_input_7(inp, out0, out1);
input [2:0] inp;
output reg [1:0] out0;
output reg [1:0] out1;
always @ (inp)
begin
case(inp)
1:
begin
out0 <= 0;
out1 <= 0;
end
2:
begin
out0 <= 0;
out1 <= 2;
end
3:
begin
out0 <= 1;
out1 <= 1;
end
4:
begin
out0 <= 0;
out1 <= 1;
end
5:
begin
out0 <= 1;
out1 <= 2;
end
6:
begin
out0 <= 1;
out1 <= 0;
end
default:
begin
out0 <= 0;
out1 <= 0;
end
endcase
end
endmodule
module atop_testbench();
reg [2:0] inp1;
reg [2:0] inp2;
wire [2:0] out;
integer i, j, l, m, k, t;
reg dummy;
integer fori, forj;
multiplication_mod_7 mul1(inp1, inp2, out);
initial
begin
k = 1;
for (fori = 0; fori < 7; fori = fori + 1)
begin
for (forj = 0; forj < 7; forj = forj + 1)
begin
inp1 = fori;
inp2 = forj;
#1 dummy = 1;
i = (fori*forj)%7;
$display ("!!! OP1 = (%d) OP2 = (%d) RES = (%d) EXPECT = (%d)", fori, forj, out, i);
l = out;
if (l != i)
begin
$display ("!!! Error (%d, %d)!!!", i, l);
end
#1 dummy = 1;
end
end
end
endmodule
2. Модулярный умножитель на базе формулы разности квадратов (на примере модуля 7)
module multiplication_mod_7(inp1, inp2, out);
input [2:0] inp1;
input [2:0] inp2;
output [2:0] out;
wire [3:0] plus;
wire [3:0] minus;
wire [2:0] plout;
wire [2:0] miout;
assign plus = inp1 + inp2; // [0; 12]
assign minus = 6 + inp1 - inp2; // [0; 12]
lut_sqr_sum ls1(plus, plout);
lut_sqr_sub ls2(minus, miout);
sub_mod_7 sub1(plout, miout, out);
endmodule
module lut_sqr_sum (in, out);
input [3:0] in;
output reg [2:0] out;
always @ (in)
begin
case (in)
0: out = 0;
1: out = 2;
2: out = 1;
3: out = 4;
4: out = 4;
5: out = 1;
6: out = 2;
7: out = 0;
8: out = 2;
9: out = 1;
10: out = 4;
11: out = 4;
12: out = 1;
default: out = 0;
endcase
end
endmodule
module lut_sqr_sub (in, out);
input [3:0] in;
output reg [2:0] out;
always @ (in)
begin
case (in)
0: out = 2;
1: out = 1;
2: out = 4;
3: out = 4;
4: out = 1;
5: out = 2;
6: out = 0;
7: out = 2;
8: out = 1;
9: out = 4;
10: out = 4;
11: out = 1;
12: out = 2;
default: out = 0;
endcase
end
endmodule
module sub_mod_7 (in1, in2, out);
input [2:0] in1, in2;
output [2:0] out;
wire [3:0] data;
assign data = 7 + in1 - in2;
mod_7_13 mdval(data, out);
endmodule
module mod_7_13 (in, out);
input [3:0] in;
output reg [2:0] out;
always @ (in)
begin
// we have small max value so we can use table here
case (in)
0: out = 0;
1: out = 1;
2: out = 2;
3: out = 3;
4: out = 4;
5: out = 5;
6: out = 6;
7: out = 0;
8: out = 1;
9: out = 2;
10: out = 3;
11: out = 4;
12: out = 5;
13: out = 6;
default: out = 0;
endcase
end
endmodule
module atop_testbench();
reg [2:0] inp1;
reg [2:0] inp2;
wire [2:0] out;
integer i, j, l, m, k, t;
reg dummy;
integer fori, forj;
multiplication_mod_7 mul1(inp1, inp2, out);
initial
begin
k = 1;
for (fori = 0; fori < 7; fori = fori + 1)
begin
for (forj = 0; forj < 7; forj = forj + 1)
begin
inp1 = fori;
inp2 = forj;
#1 dummy = 1;
i = (fori*forj)%7;
$display ("!!! OP1 = (%d) OP2 = (%d) RES = (%d) EXPECT = (%d)", fori, forj, out, i);
l = out;
if (l != i)
begin
$display ("!!! Error (%d, %d)!!!", i, l);
end
#1 dummy = 1;
end
end
end
endmodule
2. Модулярный сумматор по методу Espresso (на примере модуля 10)
module mul_mod10 (out, a, b); input [3:0] a, b; output [3:0] out; assign out[3] = (~a[3]&~a[2]&~a[1]&a[0]&b[3]) | (~a[2]&a[1]&~a[0]&b[3]&b[0]) | (a[3]&~b[3]&~b[2]&~b[1]&b[0]) | (a[2]&a[1]&~a[0]&b[3]&~b[0]) | (a[3]&~a[0]&b[2]&b[1]&~b[0]) | (a[3]&a[0]&~b[2]&b[1]&~b[0]) | (a[2]&a[1]&a[0]&b[2]&b[1]&b[0]) | (a[2]&~a[1]&~a[0]&b[2]&b[1]&b[0]) | (~a[2]&a[1]&a[0]&~b[2]&b[1]&b[0]) | (a[2]&a[1]&~a[0]&~b[2]&b[1]&b[0]) | (~a[2]&a[1]&a[0]&b[2]&b[1]&~b[0]) | (a[2]&~a[1]&~a[0]&~b[2]&b[1]&~b[0]) | (a[2]&a[1]&a[0]&b[2]&~b[1]&~b[0]) | (~a[2]&a[1]&~a[0]&b[2]&~b[1]&~b[0]); assign out[2] = (~a[2]&a[1]&a[0]&b[3]) | (a[3]&~a[0]&~b[2]&b[1]) | (a[2]&~a[1]&a[0]&b[0]) | (a[3]&~a[0]&b[1]&b[0]) | (a[3]&~b[2]&b[1]&b[0]) | (a[0]&b[2]&~b[1]&b[0]) | (~a[2]&a[1]&b[3]&~b[0]) | (a[1]&a[0]&b[3]&~b[0]) | (a[3]&~a[0]&b[3]&~b[0]) | (a[2]&~a[0]&b[2]&~b[0]) | (~a[2]&a[1]&~a[0]&b[1]&b[0]) | (a[1]&a[0]&~b[2]&b[1]&~b[0]) | (~a[3]&~a[2]&~a[1]&a[0]&b[2]) | (a[2]&~a[0]&~b[2]&~b[1]&b[0]) | (a[2]&~b[3]&~b[2]&~b[1]&b[0]) | (~a[2]&~a[1]&a[0]&b[2]&~b[0]) | (~a[2]&a[1]&~b[2]&b[1]&~b[0]); assign out[1] = (a[2]&a[1]&a[0]&b[3]) | (a[2]&~a[1]&~a[0]&b[3]) | (a[3]&~a[0]&b[3]&b[0]) | (a[3]&b[2]&b[1]&b[0]) | (a[3]&a[0]&b[3]&~b[0]) | (a[3]&b[2]&~b[1]&~b[0]) | (~a[3]&~a[2]&~a[1]&a[0]&b[1]) | (a[2]&a[1]&~a[0]&b[2]&b[1]) | (a[1]&~b[3]&~b[2]&~b[1]&b[0]) | (~a[2]&a[1]&~a[0]&b[3]&~b[0]) | (a[2]&a[1]&~a[0]&b[1]&~b[0]) | (a[2]&a[1]&b[2]&b[1]&~b[0]) | (a[1]&~a[0]&b[2]&b[1]&~b[0]) | (a[3]&~a[0]&~b[2]&b[1]&~b[0]) | (a[2]&~a[1]&~a[0]&~b[2]&b[1]&b[0]) | (~a[2]&a[1]&a[0]&b[2]&~b[1]&~b[0]) | (a[2]&~a[1]&~a[0]&b[2]&~b[1]&~b[0]) | (~a[2]&~a[1]&a[0]&b[1]&b[0]) | (a[1]&a[0]&~b[2]&~b[1]&b[0]) | (~a[2]&a[1]&~a[0]&~b[2]&b[1]&b[0]) | (~a[2]&a[1]&a[0]&~b[2]&b[1]&~b[0]); assign out[0] = (a[0]&b[0]); endmodule
Библиотека стандартных ячеек
NangateOpenCellLibrary.lib
Скрипт для запуска
lappend search_path "../libs" "../src" set target_library "NangateOpenCellLibrary.db" set link_library [list "*" $target_library] analyze -f <имя модуля>.v elaborate <имя модуля> uniquify current_design <имя модуля> check_design set_load [load_of [get_lib_pins NangateOpenCellLibrary/INV_X4/A]] [all_outputs] set_driving_cell -lib_cell DFFRS_X2 -library NangateOpenCellLibrary -pin Q [all_inputs] set_max_delay -to [all_outputs] 0 set_max_area 0 compile report_timing > result/timing_<имя модуля>.rpt report_area > result/area_<имя модуля>.rpt remove_design -all
Файлы для эксперимента
- Несжатые таблицы истинности для умножителей (.csv, 8MB)
- Сжатые Espresso таблицы истинности для умножителей (.csv, 4MB)
- Verilog на основе таблиц истинности для умножителей (.v, 4.3MB)