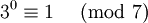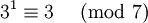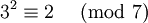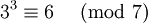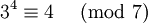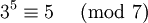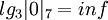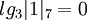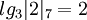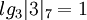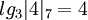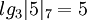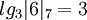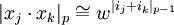Модулярная логарифметика — различия между версиями
Turbo (обсуждение | вклад) |
Turbo (обсуждение | вклад) |
||
| Строка 35: | Строка 35: | ||
:<math>lg_{3}|5|_{7} = 5</math> | :<math>lg_{3}|5|_{7} = 5</math> | ||
:<math>lg_{3}|6|_{7} = 3</math> | :<math>lg_{3}|6|_{7} = 3</math> | ||
| + | |||
| + | == Варианты использования == | ||
| + | |||
| + | Исходя из понятия первообразного корня операция умножения по модулю <math>p</math> в [[Система остаточных классов|модулярной арифметике]] может быть отображена на операцию сложения по модулю <math>p-1</math> по следующей формуле: | ||
| + | :<math>|x_{j}\cdot x_{k}|_{p} \cong w^{|i_{j}+i_{k}|_{p-1}}</math> | ||
Версия 15:01, 3 июня 2013
Модулярная логарифметика (более полное название Логарифмическая система остаточных классов, в английском варианте The Residue Logarithmic Number System) - система счисления основанная на системе остаточных классов, в которой числа представлены в виде дискретных логарифмов от соответствующих вычетов.
Первообразный корень
Первообразным корнем 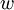 по модулю
по модулю  (другое название примитивный корень) называется целое число, возведение, которого в степень
(другое название примитивный корень) называется целое число, возведение, которого в степень 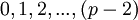 дает неповторяющиеся вычеты по модулю
дает неповторяющиеся вычеты по модулю  .
.
Замечание: Первообразный корень в нашей нотации существует только в случае если  - простое число.
- простое число.
Пример: Число 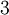 является первообразным корнем по модулю
является первообразным корнем по модулю 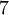 . Чтобы в этом убедиться, достаточно каждое число от
. Чтобы в этом убедиться, достаточно каждое число от 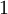 до
до 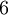 представить как некоторую степень тройки по модулю
представить как некоторую степень тройки по модулю 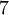 :
:
Дискретный логарифм
Пусть 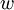 – первообразный корень конечного поля
– первообразный корень конечного поля 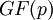 . Дискретным логарифмом по основанию
. Дискретным логарифмом по основанию 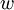 над
над 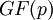 будем называть функцию аргумента
будем называть функцию аргумента  , заданную формулой:
, заданную формулой:
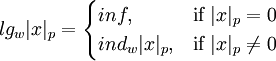
здесь:
-
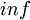 - элемент не являющийся элементом кольца
- элемент не являющийся элементом кольца 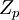 , так называемая "сингулярность"
, так называемая "сингулярность"
-
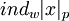 - индекс вычета
- индекс вычета 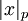 , такой что
, такой что 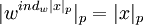
Пример: Найдем дискретные логарифмы для 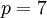
Варианты использования
Исходя из понятия первообразного корня операция умножения по модулю  в модулярной арифметике может быть отображена на операцию сложения по модулю
в модулярной арифметике может быть отображена на операцию сложения по модулю 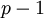 по следующей формуле:
по следующей формуле: