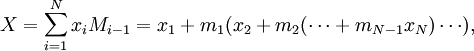Полиадический код — различия между версиями
Turbo (обсуждение | вклад) (Новая страница: «'''Полиадический код''' (или система счисления со смешанным основанием от англ. [http://en.wikipedia…») |
Turbo (обсуждение | вклад) |
||
| Строка 10: | Строка 10: | ||
* Сравнения чисел | * Сравнения чисел | ||
* Перевода чисел из системы остаточных классов в обычную позиционную систему счисления | * Перевода чисел из системы остаточных классов в обычную позиционную систему счисления | ||
| + | |||
| + | == Обратное преобразование == | ||
| + | |||
| + | Обратное преобразование на базе полиадического кода, базируется на идее, что любое число X может быть представлено в системе взаимно простых чисел <math>p_1,\ldots, p_n</math>, как [1]: | ||
| + | :<math>X = a_1 + a_2\cdot p_1 + a_3\cdot p_1\cdot p_2 + ... + a_{n-1}\cdot p_1\cdot p_2\cdot \ldots\cdot p_{n-2} + a_n\cdot p_1\cdot p_2\cdot \ldots\cdot p_{n-1}</math>, где <math>0 < a_i < p_i</math> | ||
| + | * <math>|X|_{p_1} = x_1 = a_1</math> | ||
| + | * <math>|X - a_1|_{p_2} = |x_2 - a_1|_{p_2} = |a_2\cdot p_1|_{p_2}</math> => a<sub>2</sub> = ((p<sub>1</sub><sup>-1</sup>)%p<sub>2</sub>*(x<sub>2</sub> - a<sub>1</sub>))%p<sub>2</sub></li> | ||
| + | <li>(X - a<sub>1</sub> - a<sub>2</sub>*p<sub>1</sub>)%p<sub>3</sub> = (a<sub>3</sub>*p<sub>1</sub>*p<sub>2</sub>)%p<sub>3</sub> => a<sub>3</sub> = ((p<sub>2</sub><sup>-1</sup>)%p<sub>3</sub>*((p<sub>1</sub><sup>-1</sup>)%p<sub>3</sub>*(x<sub>3</sub> - a<sub>1</sub>) - a<sub>2</sub>))%p<sub>3</sub></li> | ||
| + | <li>…</li> | ||
| + | </ul> | ||
| + | Для использования этого метода требуются константы вида (p<sub>i</sub><sup>-1</sup>)%p<sub>k</sub><sup>-1</sup>. Можно также заметить, что начинать вычисление a<sub>3</sub> можно, как только появилось значение a<sub>1</sub>. На основе этого метода можно строить конвеерные преобразователи. | ||
| + | |||
| + | == Ссылки == | ||
| + | [1] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York. | ||
Версия 09:08, 15 июля 2013
Полиадический код (или система счисления со смешанным основанием от англ. associated mixed radix system (AMRS))
Любое число 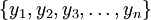 в системе остаточных классов может быть представленно в виде полиадического кода
в системе остаточных классов может быть представленно в виде полиадического кода
где
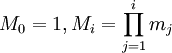 для
для 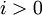 и
и 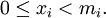
Полиадический код используется для:
- Сравнения чисел
- Перевода чисел из системы остаточных классов в обычную позиционную систему счисления
Обратное преобразование
Обратное преобразование на базе полиадического кода, базируется на идее, что любое число X может быть представлено в системе взаимно простых чисел 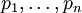 , как [1]:
, как [1]:
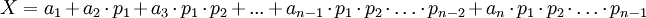 , где
, где 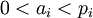
-
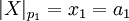
-
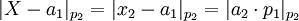 => a2 = ((p1-1)%p2*(x2 - a1))%p2</li>
=> a2 = ((p1-1)%p2*(x2 - a1))%p2</li>
</ul> Для использования этого метода требуются константы вида (pi-1)%pk-1. Можно также заметить, что начинать вычисление a3 можно, как только появилось значение a1. На основе этого метода можно строить конвеерные преобразователи.
Ссылки
[1] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York.