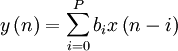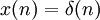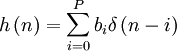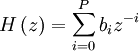Фильтр с конечной импульсной характеристикой — различия между версиями

Материал из Модулярная арифметики
Перейти к: навигация, поиск
(Новая страница: «'''Фильтр с конечной импульсной характеристикой''' ('''Нерекурсивный фильтр''', '''КИХ-фильтр'…»)
 
Строка 25: Строка 25:
 
== Пример программы ==
 
== Пример программы ==
 
Ниже приведен пример программы КИХ-фильтра, написанный на C :
 
Ниже приведен пример программы КИХ-фильтра, написанный на C :
−
<source lang='c'>
+
<pre>
  
 
#define N 100 // порядок фильтра
 
#define N 100 // порядок фильтра
Строка 53: Строка 53:
 
}
 
}
  
−
</source>
+
</pre>
  
 +
== Построение КИХ-фильтров ==
  
 
== Ссылки ==
 
== Ссылки ==
 
* [http://www.dsplib.ru/content/filters/fir/fir.html Расчет КИХ фильтра с линейной фазочастотной характеристикой методом частотной выборки]
 
* [http://www.dsplib.ru/content/filters/fir/fir.html Расчет КИХ фильтра с линейной фазочастотной характеристикой методом частотной выборки]
 
* [http://www.dspguru.com/dsp/faqs/fir FIR FAQ]
 
* [http://www.dspguru.com/dsp/faqs/fir FIR FAQ]

Версия 12:44, 15 июля 2013

Фильтр с конечной импульсной характеристикой (Нерекурсивный фильтр, КИХ-фильтр) или FIR-фильтр (FIR сокр. от finite impulse response — конечная импульсная характеристика) — один из видов линейных цифровых фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какого-то момента времени она становится точно равной нулю). Такой фильтр называют ещё нерекурсивным из-за отсутствия обратной связи. Знаменатель передаточной функции такого фильтра — некая константа.

Динамические характеристики

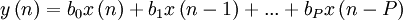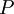Разностное уравнение, описывающее связь между входным и выходным сигналами фильтра: y\left (n\right)=b_0 x\left(n\right)+ b_1 x\left(n-1 \right)+...+b_P x\left(n-P \right) где P — порядок фильтра, 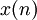x(n) — входной сигнал, 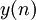y(n) — выходной сигнал, а 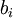b_{i} — коэффициенты фильтра. Иными словами, значение любого отсчета выходного сигнала определяется суммой масштабированных значений P предыдущих отсчетов. 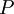Можно сказать иначе: значение выхода фильтра в любой момент времени есть значение отклика на мгновенное значение входа и сумма всех постепенно затухающих откликов P предыдущих отсчетов сигнала, которые всё ещё оказывают влияние на выход (после P-отсчетов импульсная переходная функция становится равной нулю, как уже было сказано, поэтому все члены после P-го тоже станут равными нулю). Запишем предыдущее уравнение в более ёмком виде:

y \left( n \right) = \sum_{i=0}^{P} b_i x \left( n-i \right)

Для того, чтобы найти ядро фильтра положим

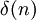x(n) = \delta(n)

где \delta(n) — дельта-функция. Тогда импульсная характеристика КИХ-фильтра может быть записана как:

h\left (n\right)=\sum_{i=0}^{P}b_i \delta\left(n-i\right)

Z-преобразование импульсной характеристики даёт нам передаточную функцию КИХ-фильтра:

H\left(z\right)=\sum_{i=0}^{P}b_i z^{-i}

Свойства

КИХ-фильтр обладает рядом полезных свойств, из-за которых он иногда более предпочтителен в использовании, чем БИХ-фильтр. Вот некоторые из них:

  • КИХ-фильтры устойчивы.
  • КИХ-фильтры при реализации не требуют наличия обратной связи.
  • Фаза КИХ-фильтров может быть сделана линейной

Прямая форма КИХ фильтра

КИХ фильтры могут быть реализованы с использованием трех элементов: умножитель, сумматор и блок задержки. Вариант, показанный на рисунке, есть прямая реализация КИХ-фильтров типа 1.

Реализация прямой формы КИХ фильтра

Пример программы

Ниже приведен пример программы КИХ-фильтра, написанный на C : 


#define N 100 // порядок фильтра
float h[N] = { #include “f1.h” }; //вставка файла с известными коэффициентами фильтра
float x[N];
float y[N];

short my_FIR(short sample_data)
{
  float result = 0;

  for ( int i = N - 2 ; i >= 0 ; i-- )
  {
    x[i + 1] = x[i];
    y[i + 1] = y[i];
  }
  
  x[0] = (float)sample_data;
  
  for (int k = 0; k < N; k++)
  {
    result = result + x[k]*h[k];
  }
  y[0] = result;

  return ((short)result);
}

Построение КИХ-фильтров

Ссылки

Источник — «https://vscripts.ru/w/index.php?title=Фильтр_с_конечной_импульсной_характеристикой&oldid=511»