Первообразный корень по модулю — различия между версиями
Материал из Модулярная арифметики
Turbo (обсуждение | вклад) (Новая страница: «== Определение == Первообразным (примитивным) корнем по модулю <math>n</math> (от английского ''prim…») |
(нет различий)
|
Текущая версия на 08:41, 9 декабря 2013
Определение
Первообразным (примитивным) корнем по модулю  (от английского primitive root modulo n) называется такое число
(от английского primitive root modulo n) называется такое число 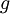 , что все его степени по модулю
, что все его степени по модулю  пробегают по всем числам, взаимно простым с
пробегают по всем числам, взаимно простым с  . Математически это формулируется таким образом: если
. Математически это формулируется таким образом: если 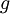 является первообразным корнем по модулю
является первообразным корнем по модулю  , то для любого целого
, то для любого целого  такого, что
такого, что  , найдётся такое целое
, найдётся такое целое 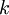 , что
, что 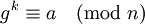 .
.
В частности, для случая простого  степени первообразного корня пробегают по всем числам от
степени первообразного корня пробегают по всем числам от 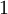 до
до 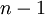 .
.
Существование
Первообразный корень по модулю  существует тогда и только тогда, когда
существует тогда и только тогда, когда  является либо степенью нечётного простого, либо удвоенной степенью простого, а также в случаях
является либо степенью нечётного простого, либо удвоенной степенью простого, а также в случаях 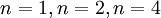 . (Доказано Гауссом в 1801)
. (Доказано Гауссом в 1801)