Система остаточных классов — различия между версиями
Bundin (обсуждение | вклад) (→Умножение) |
Bundin (обсуждение | вклад) (→Сложение и вычитание) |
||
| Строка 9: | Строка 9: | ||
=== Сложение и вычитание === | === Сложение и вычитание === | ||
| − | Пусть <math>A,B</math>- произвольные натуральные числа. Положим, что <math>A,B</math> представляются в виде системы остаточных классов как <math>(a_1,\ldots ,a_n)</math> и <math>(b_1,\ldots b_n)</math> соответственно. Формально, <math>\varphi^{-1}(a_1,\ldots ,a_n)=A, \varphi^{-1}(b_1,\ldots b_n)=B</math>. В силу того, что <math>\varphi</math>- изоморфизм | + | Пусть <math>A,B</math>- произвольные натуральные числа. Положим, что <math>A,B</math> представляются в виде системы остаточных классов как <math>(a_1,\ldots ,a_n)</math> и <math>(b_1,\ldots b_n)</math> соответственно. Формально, <math>\varphi^{-1}(a_1,\ldots ,a_n)=A, \varphi^{-1}(b_1,\ldots b_n)=B</math>. В силу того, что <math>\varphi</math>- изоморфизм будем иметь <math>\varphi^{-1}((a_1,\ldots ,a_n)+(b_1,\ldots b_n))=\varphi^{-1}(a_1,\ldots ,a_n)+\varphi^{-1}(b_1,\ldots b_n)</math>. Обозначим через <math>C</math> остаток <math>A+B</math> от деления на <math>M</math>. Тогда <math>C</math> представляется в виде системы остаточных классов как <math>(a_1+b_1,\ldots ,a_n+b_n)</math>. |
=== Умножение === | === Умножение === | ||
Версия 03:51, 26 января 2013
Система остаточных классов используется для представления больших чисел N, обеспечивая таким образом более эффективные вычисления. В основе данного представления лежит изоморфизм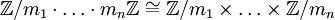 
, который доставляет китайская теорема об остатках.
Содержание
Основные определения
Системой остаточных классов называют произвольное конечное множество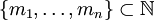 
, такое что 
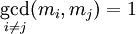, где 
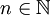. Пусть задана произвольная система остаточных классов 
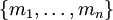и положим, что 
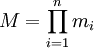. Тогда имеем эпиморфизм колец 
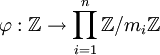, т.ч. 
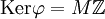, который индуцирует канонический изоморфизм 
.
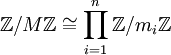Выполнение арифметических операций
С использованием системы остаточных классов можно выполнять основные арифметические операции.
Сложение и вычитание
Пусть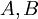 
- произвольные натуральные числа. Положим, что 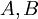представляются в виде системы остаточных классов как 
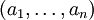и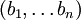 
соответственно. Формально, 
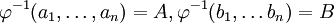. В силу того, что 
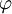- изоморфизм будем иметь 
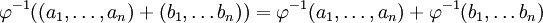. Обозначим через 
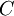остаток 
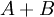от деления на 
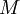. Тогда 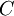представляется в виде системы остаточных классов как 
.
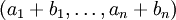Умножение
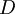- остаток от деления 
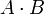на 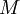. Тогда 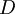представляется в виде системы остаточных классов в виде 
.
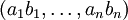Деление
Деление 
на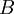 
с использованием системы остаточных классов можно выполнять не всегда. Положим, что 
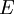- остаток 
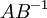от деления на 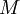. На языке теории колец это означает, что 
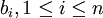обратим и 
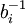- обратный. Тогда 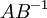представляется в виде 
.
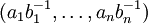Факторизация полупростых чисел
Пусть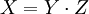 
- полупростое число. Рассмотрим систему остаточных классов 
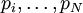, где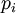 
— 
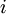-е простое число.
