Участник:Nikz — различия между версиями
Материал из Модулярная арифметики
NikZ (обсуждение | вклад) |
NikZ (обсуждение | вклад) |
||
| Строка 4: | Строка 4: | ||
== Теоретические основы алгоритма == | == Теоретические основы алгоритма == | ||
=== Поля Галуа === | === Поля Галуа === | ||
| − | Операцию сложения определим как «исключающее ИЛИ»(XOR).Очевидно, что в таком случае операция сложения является обратной самой себе. Тогда операция умножения в двоичном виде будет выглядеть так: | + | Операцию сложения определим как «исключающее ИЛИ»(XOR).Очевидно, что в таком случае операция сложения является обратной самой себе. Тогда операция умножения в двоичном виде будет выглядеть так: |
| + | |||
| + | <math> \begin{matrix} *\underline{\begin{matrix} | ||
0 & 0 & 0 & 1 & 1 \\ | 0 & 0 & 0 & 1 & 1 \\ | ||
0 & 0 & 1 & 1 & 0 \\ | 0 & 0 & 1 & 1 & 0 \\ | ||
| + | \end{matrix}}\\ | ||
| + | +\underline{\begin{matrix} | ||
0 & 0 & 1 & 1 & 0 \\ | 0 & 0 & 1 & 1 & 0 \\ | ||
| + | 0 & 1 & 1 & 0 & 0 \\ | ||
| + | \end{matrix}} \\ | ||
| + | \begin{matrix} | ||
| + | & 0 & 1 & 0 & 1 & 0 \\ | ||
| + | \end{matrix} | ||
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
| + | |||
| + | Так можно умножать полиномы, в данном случае мы умножили: | ||
| + | <math> (x + 1) * (x^2 + x) = x^3 + x</math>. | ||
Версия 10:15, 19 мая 2014
Постановка задачи
В данной статье разбирается пример работы алгоритма коррекции ошибки для 16-битных строк. Строка разбивает на блоки длиной 4 бита и каждый блок представляет собой элемент поля Галуа GF16. Необходимо отследить и исправить одиночную ошибку, внесённую в один из блоков.
Теоретические основы алгоритма
Поля Галуа
Операцию сложения определим как «исключающее ИЛИ»(XOR).Очевидно, что в таком случае операция сложения является обратной самой себе. Тогда операция умножения в двоичном виде будет выглядеть так:

Так можно умножать полиномы, в данном случае мы умножили:
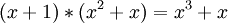 .
.