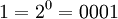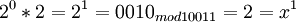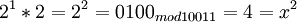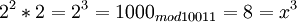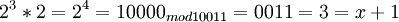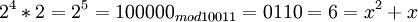Участник:Nikz — различия между версиями
NikZ (обсуждение | вклад) |
NikZ (обсуждение | вклад) |
||
| Строка 16: | Строка 16: | ||
\begin{matrix} | \begin{matrix} | ||
& 0 & 1 & 0 & 1 & 0 \\ | & 0 & 1 & 0 & 1 & 0 \\ | ||
| − | \end{matrix} | + | \end{matrix} \\ |
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
| Строка 22: | Строка 22: | ||
Так можно умножать полиномы, в данном случае мы умножили: | Так можно умножать полиномы, в данном случае мы умножили: | ||
<math> (x + 1) * (x^2 + x) = x^3 + x</math>. | <math> (x + 1) * (x^2 + x) = x^3 + x</math>. | ||
| + | Определим также операцию деления чисел(или полиномов) с остатком – по аналогичным правилам, например: | ||
| + | <math> \frac{110010}{101011}=011001 </math> | ||
| + | или <math> \frac{x^5 + x^4 + x}{x^5 + x^3 + x + 1} = x^4 + x^3 + 1 </math> | ||
| + | Теперь построим поле из 16 элементов <math> GF_{16} </math>. Операцию сложения определена на XOR, Операция деления дополнена получением остатка по некоторому модулю. | ||
| + | Выберем в качестве модуля неприводимый полином <math> x^4+x+1 (10011) </math>.<br /> | ||
| + | |||
| + | Возьмем единицу и будем последовательно умножать ее на 2 и рассмотрим числа, которые будут при этом | ||
| + | # <math>1= 2^0=0001 </math> | ||
| + | # <math> 2^0*2=2^1=0010 _{mod 10011} = 2 = x^1 </math> | ||
| + | # <math> 2^1*2=2^2=0100 _{mod 10011} = 4 = x^2 </math> | ||
| + | # <math> 2^2*2=2^3=1000 _{mod 10011} = 8 = x^3 </math> | ||
| + | # <math> 2^3*2=2^4=10000 _{mod 10011} = 0011 = 3 = x+1 </math> | ||
| + | # <math> 2^4*2=2^5=100000 _{mod 10011} = 0110 = 6 = x^2+x </math> | ||
| + | и так далее.<br /> | ||
| + | '''Составим таблицу умножения'''<br /> | ||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |- | ||
| + | ! Степень | ||
| + | ! Результат | ||
| + | |- | ||
| + | | 0 | ||
| + | | 1 | ||
| + | | 0001 | ||
| + | |- | ||
| + | | 1 | ||
| + | | 2 | ||
| + | | 0010 | ||
| + | |- | ||
| + | | 2 | ||
| + | | 4 | ||
| + | | 0100 | ||
| + | |- | ||
| + | | 3 | ||
| + | | 8 | ||
| + | | 1000 | ||
| + | |- | ||
| + | | 4 | ||
| + | | 3 | ||
| + | | 0011 | ||
| + | |- | ||
| + | | 5 | ||
| + | | 6 | ||
| + | | 0110 | ||
| + | |- | ||
| + | | 6 | ||
| + | | 12 | ||
| + | | 1100 | ||
| + | |- | ||
| + | | 7 | ||
| + | | 11 | ||
| + | | 1011 | ||
| + | |- | ||
| + | | 8 | ||
| + | | 5 | ||
| + | | 0101 | ||
| + | |- | ||
| + | | 9 | ||
| + | | 10 | ||
| + | | 1010 | ||
| + | |- | ||
| + | | 10 | ||
| + | | 7 | ||
| + | | 0111 | ||
| + | |- | ||
| + | | 11 | ||
| + | | 14 | ||
| + | | 1110 | ||
| + | |- | ||
| + | | 12 | ||
| + | | 15 | ||
| + | | 1111 | ||
| + | |- | ||
| + | | 13 | ||
| + | | 13 | ||
| + | | 1101 | ||
| + | |- | ||
| + | | 14 | ||
| + | | 9 | ||
| + | | 1001 | ||
| + | |- | ||
| + | | 15 | ||
| + | | 1 | ||
| + | | 0001 | ||
| + | |} | ||
Версия 11:13, 19 мая 2014
Постановка задачи
В данной статье разбирается пример работы алгоритма коррекции ошибки для 16-битных строк. Строка разбивает на блоки длиной 4 бита и каждый блок представляет собой элемент поля Галуа GF16. Необходимо отследить и исправить одиночную ошибку, внесённую в один из блоков.
Теоретические основы алгоритма
Поля Галуа
Операцию сложения определим как «исключающее ИЛИ»(XOR).Очевидно, что в таком случае операция сложения является обратной самой себе. Тогда операция умножения в двоичном виде будет выглядеть так:

Так можно умножать полиномы, в данном случае мы умножили:
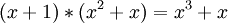 .
Определим также операцию деления чисел(или полиномов) с остатком – по аналогичным правилам, например:
.
Определим также операцию деления чисел(или полиномов) с остатком – по аналогичным правилам, например:
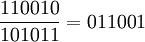 или
или 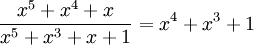 Теперь построим поле из 16 элементов
Теперь построим поле из 16 элементов 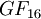 . Операцию сложения определена на XOR, Операция деления дополнена получением остатка по некоторому модулю.
Выберем в качестве модуля неприводимый полином
. Операцию сложения определена на XOR, Операция деления дополнена получением остатка по некоторому модулю.
Выберем в качестве модуля неприводимый полином 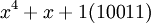 .
.
Возьмем единицу и будем последовательно умножать ее на 2 и рассмотрим числа, которые будут при этом
и так далее.
Составим таблицу умножения
| Степень | Результат | |
|---|---|---|
| 0 | 1 | 0001 |
| 1 | 2 | 0010 |
| 2 | 4 | 0100 |
| 3 | 8 | 1000 |
| 4 | 3 | 0011 |
| 5 | 6 | 0110 |
| 6 | 12 | 1100 |
| 7 | 11 | 1011 |
| 8 | 5 | 0101 |
| 9 | 10 | 1010 |
| 10 | 7 | 0111 |
| 11 | 14 | 1110 |
| 12 | 15 | 1111 |
| 13 | 13 | 1101 |
| 14 | 9 | 1001 |
| 15 | 1 | 0001 |