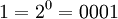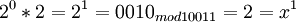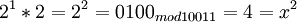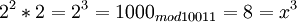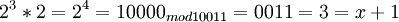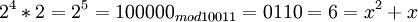Участник:Nikz — различия между версиями
NikZ (обсуждение | вклад) |
NikZ (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| + | = Пример коррекции ошибки с помощью кодов Рида - Соломона = | ||
== Постановка задачи == | == Постановка задачи == | ||
В данной статье разбирается пример работы алгоритма коррекции ошибки для 16-битных строк. Строка разбивает на блоки длиной 4 бита и каждый блок представляет собой элемент поля Галуа GF<sub>16</sub>. Необходимо отследить и исправить одиночную ошибку, внесённую в один из блоков. | В данной статье разбирается пример работы алгоритма коррекции ошибки для 16-битных строк. Строка разбивает на блоки длиной 4 бита и каждый блок представляет собой элемент поля Галуа GF<sub>16</sub>. Необходимо отследить и исправить одиночную ошибку, внесённую в один из блоков. | ||
| Строка 4: | Строка 5: | ||
== Теоретические основы алгоритма == | == Теоретические основы алгоритма == | ||
=== Поля Галуа === | === Поля Галуа === | ||
| − | Операцию сложения определим как | + | Операцию сложения определим как "исключающее ИЛИ" <math>(XOR)</math>.Очевидно, что в таком случае операция сложения является обратной самой себе. Тогда операция умножения в двоичном виде будет выглядеть так: |
<math> \begin{matrix} *\underline{\begin{matrix} | <math> \begin{matrix} *\underline{\begin{matrix} | ||
| Строка 111: | Строка 112: | ||
'''Таким образом, получили поле <math>GF_{16}</math>, то есть для двоичных 4-разрядных чисел.''' | '''Таким образом, получили поле <math>GF_{16}</math>, то есть для двоичных 4-разрядных чисел.''' | ||
| + | == Коды Рида - Соломона == | ||
| + | При построении кода Рида-Соломона задается пара чисел N,K, где N-Общее количество символов, а К- «полезное» количество символов, N-K символов задают избыточный код, предназначенный для восстановления ошибок. | ||
| + | Такой код Рида-Соломона будет иметь «расстояние Хемминга» <math>D=N-K+1</math>. | ||
| + | В соответствии с теорией кодирования, код, имеющий расстояние Хемминга <math>D=2t+1</math>, позволяет восстанавливать t ошибок. Таким образом, если нам необходимо восстановить t ошибок, то общее количество символов сообщения <math>N=K+2t</math>. | ||
| + | Сообщения при кодировании Рида-Соломона представляются полиномами. | ||
| + | Исходное сообщение представляется как коэффициенты полинома <math>p(x)</math> степени <math>K-1</math>, имеющего <math>K</math> коэффициентов.<br /> | ||
| + | Порождающий многочлен Рида-Соломона,<math>g(x)</math>, строится следующий образом: | ||
| + | <math> g(x)=(x+2)(x+2^{2})..(x+2^{ D-1 } ) </math>, <math>2 - </math> примитивный член поля. Нетрудно понять, что <math>2^{1},2^{2},..,2^{D-1}</math> - корни этого многочлена.<br> | ||
| + | Например, построим порождающий многочлен кода Рида-Соломона с <math>N=15,K=9</math>, способного исправлять до 3 ошибок <math>(15-9)/2=3</math>: | ||
| + | <math>g(x)=(x+2)(x+2^{2} )(x+2^{3} )(x+2^{4} )(x+2^{5} )(x+2^{6} )=x^{6}+7x^{5}+9x^{4}+3x^{3}+12x^{2}+10x+12</math>. ''(Возведение в степень и умножения выполнены над полем GF<sub>16</sub> )!'' | ||
Версия 21:31, 13 июня 2014
Содержание
Пример коррекции ошибки с помощью кодов Рида - Соломона
Постановка задачи
В данной статье разбирается пример работы алгоритма коррекции ошибки для 16-битных строк. Строка разбивает на блоки длиной 4 бита и каждый блок представляет собой элемент поля Галуа GF16. Необходимо отследить и исправить одиночную ошибку, внесённую в один из блоков.
Теоретические основы алгоритма
Поля Галуа
Операцию сложения определим как "исключающее ИЛИ" 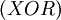 .Очевидно, что в таком случае операция сложения является обратной самой себе. Тогда операция умножения в двоичном виде будет выглядеть так:
.Очевидно, что в таком случае операция сложения является обратной самой себе. Тогда операция умножения в двоичном виде будет выглядеть так:

Так можно умножать полиномы, в данном случае мы умножили:
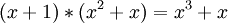 .
Определим также операцию деления чисел(или полиномов) с остатком – по аналогичным правилам, например:
.
Определим также операцию деления чисел(или полиномов) с остатком – по аналогичным правилам, например:
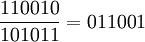 или
или 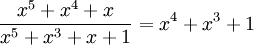 Теперь построим поле из 16 элементов
Теперь построим поле из 16 элементов 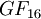 . Операцию сложения определена на XOR, Операция деления дополнена получением остатка по некоторому модулю.
Выберем в качестве модуля неприводимый полином
. Операцию сложения определена на XOR, Операция деления дополнена получением остатка по некоторому модулю.
Выберем в качестве модуля неприводимый полином 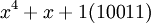 .
.
Возьмем единицу и будем последовательно умножать ее на 2 и рассмотрим числа, которые будут при этом
и так далее.
Составим таблицу умножения
| Степень | Результат | |
|---|---|---|
| 0 | 1 | 0001 |
| 1 | 2 | 0010 |
| 2 | 4 | 0100 |
| 3 | 8 | 1000 |
| 4 | 3 | 0011 |
| 5 | 6 | 0110 |
| 6 | 12 | 1100 |
| 7 | 11 | 1011 |
| 8 | 5 | 0101 |
| 9 | 10 | 1010 |
| 10 | 7 | 0111 |
| 11 | 14 | 1110 |
| 12 | 15 | 1111 |
| 13 | 13 | 1101 |
| 14 | 9 | 1001 |
| 15 | 1 | 0001 |
Таким образом, при дальнейшем умножении весь цикл повторится снова. Полученные степени двойки не сложно умножать между собой, например: 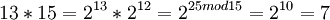 . Можно проверить результат,разделив
. Можно проверить результат,разделив 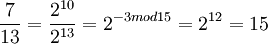 .
.
Таким образом, получили поле 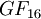 , то есть для двоичных 4-разрядных чисел.
, то есть для двоичных 4-разрядных чисел.
Коды Рида - Соломона
При построении кода Рида-Соломона задается пара чисел N,K, где N-Общее количество символов, а К- «полезное» количество символов, N-K символов задают избыточный код, предназначенный для восстановления ошибок.
Такой код Рида-Соломона будет иметь «расстояние Хемминга» 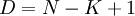 .
В соответствии с теорией кодирования, код, имеющий расстояние Хемминга
.
В соответствии с теорией кодирования, код, имеющий расстояние Хемминга 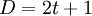 , позволяет восстанавливать t ошибок. Таким образом, если нам необходимо восстановить t ошибок, то общее количество символов сообщения
, позволяет восстанавливать t ошибок. Таким образом, если нам необходимо восстановить t ошибок, то общее количество символов сообщения 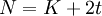 .
Сообщения при кодировании Рида-Соломона представляются полиномами.
Исходное сообщение представляется как коэффициенты полинома
.
Сообщения при кодировании Рида-Соломона представляются полиномами.
Исходное сообщение представляется как коэффициенты полинома 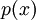 степени
степени 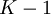 , имеющего
, имеющего 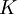 коэффициентов.
коэффициентов.
Порождающий многочлен Рида-Соломона,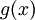 , строится следующий образом:
, строится следующий образом:
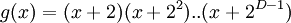 ,
, 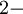 примитивный член поля. Нетрудно понять, что
примитивный член поля. Нетрудно понять, что 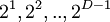 - корни этого многочлена.
- корни этого многочлена.
Например, построим порождающий многочлен кода Рида-Соломона с 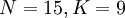 , способного исправлять до 3 ошибок
, способного исправлять до 3 ошибок 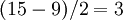 :
:
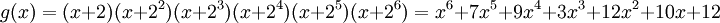 . (Возведение в степень и умножения выполнены над полем GF16 )!
. (Возведение в степень и умножения выполнены над полем GF16 )!