Теорема о делении с остатком. Алгоритм Евклида
Материал из Модулярная арифметики
Версия от 12:44, 10 декабря 2014; Isaeva (обсуждение | вклад)
Пример
Пусть модуль 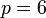 .
.
Тогда имеем шесть классов разбиения множества целых чисел по модулю 6:
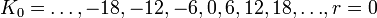 ;
;
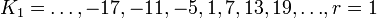 ;
;
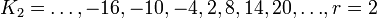 ;
;
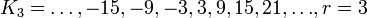 ;
;
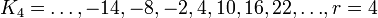 ;
;
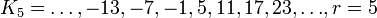 ,
,
где через  обозначен остаток от деления целого числа на 6.
обозначен остаток от деления целого числа на 6.