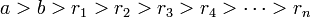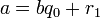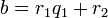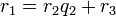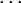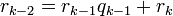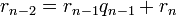Теорема о делении с остатком. Алгоритм Евклида
Напомним теорему о делении с остатком:
Теорема о делении с остатком
Для любых целых  и
и  ,
, 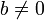 , существует единственный набор целых чисел
, существует единственный набор целых чисел 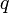 и
и  , что
, что 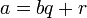 и
и 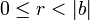 , где
, где 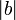 — модуль числа
— модуль числа  .
.
Легко доказывается, что для любых целых чисел  и
и  ,
, 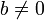 деление с остатком возможно и числа
деление с остатком возможно и числа 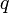 и
и  определяются однозначно.
определяются однозначно.
Рассмотрим следующий пример:
Пример
Пусть модуль 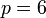 .
.
Тогда имеем шесть классов разбиения множества целых чисел по модулю 6:
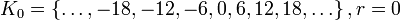 ;
;
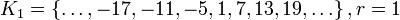 ;
;
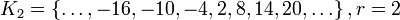 ;
;
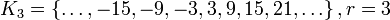 ;
;
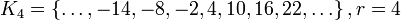 ;
;
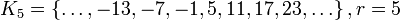 ,
,
где через  обозначен остаток от деления целого числа на 6.
обозначен остаток от деления целого числа на 6.
В данном примере полная система наименьших неотрицательных вычетов есть множество 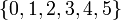 ; полная система наименьших положительных вычетов – множество
; полная система наименьших положительных вычетов – множество 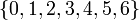 ; полная система наименьших по абсолютной величине вычетов – множество
; полная система наименьших по абсолютной величине вычетов – множество 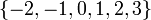 ; приведённая система вычетов – множество
; приведённая система вычетов – множество 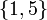 , так как
, так как 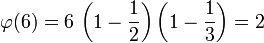 ; фактор-множество
; фактор-множество 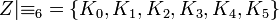 .
.
Один из методов выполнения арифметических операций над целыми числами основан на простых положениях теории чисел. Идея этого метода состоит в том, что целые числа представляются в одной из непозиционных систем – в системе остаточных классов. А именно: вместо операций над целыми числами оперируют с остатками от деления этих чисел на заранее выбранные числа – модули 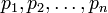 .
Чаще всего модули
.
Чаще всего модули 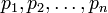 выбирают из множества простых чисел.
выбирают из множества простых чисел.
Пусть
-
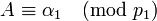 ,
,
-
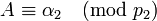 ,
,
-
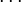 ,
,
-
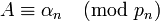 .
.
Так как в кольце целых чисел имеет место теорема о делении с остатком, т. е. 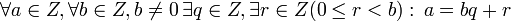 , то кольцо Z, по определению, является евклидовым. Таким образом, в качестве чисел
, то кольцо Z, по определению, является евклидовым. Таким образом, в качестве чисел 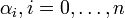 можно выбрать остатки от деления числа
можно выбрать остатки от деления числа 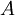 на
на 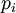 соответственно.
соответственно.
Рассмотрим гомоморфное отображение:
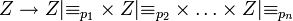 .
.
Тогда каждому целому числу А можно поставить в соответствие кортеж 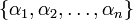 наименьших неотрицательных вычетов по одному из соответствующих классов.
наименьших неотрицательных вычетов по одному из соответствующих классов.
Важно отметить, что при преобразовании числа нет потери информации, если выполнено условие 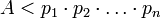 , поскольку всегда, зная
, поскольку всегда, зная 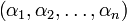 можно восстановить само число
можно восстановить само число 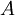 . Поэтому кортеж можно рассматривать как один из способов представления целого числа
. Поэтому кортеж можно рассматривать как один из способов представления целого числа 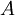 – модулярное представление, или представление в системе остаточных классов (СОК).
– модулярное представление, или представление в системе остаточных классов (СОК).
Для дальнейшего используем расширенный алгоритм Евклида или его аналог – алгоритм нахождения линейного представления наибольшего общего делителя целых чисел: если числа а и b одновременно не равны нулю, то существуют целые числа 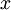 и
и 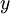 , такие, что
, такие, что 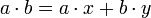 .
.
Действительно, пусть 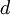 – наименьшее целое положительное число вида
– наименьшее целое положительное число вида 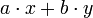 , например,
, например, 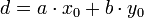 , где числа
, где числа 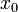 и
и 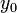 не обязательно определены однозначно. Существование числа
не обязательно определены однозначно. Существование числа 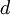 следует только из принципа полной упорядоченности. Очевидно, что
следует только из принципа полной упорядоченности. Очевидно, что 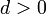 . Остаётся показать, что
. Остаётся показать, что 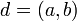 . Для этого надо проверить выполнение двух условий: а)
. Для этого надо проверить выполнение двух условий: а) 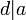 и
и 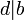 б) если
б) если 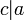 и
и 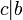 то
то 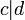 .
.
От противного: допустим, что свойство а) не выполняется, для определенности положим, что не выполнено 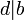 . Тогда по теореме о делении с остатком
. Тогда по теореме о делении с остатком 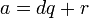 ,
, 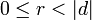 , и, следовательно,
, и, следовательно,
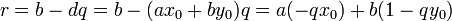 ,
,
что противоречит минимальности 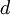 .
.
Выполнение свойства б) проверяется непосредственно:
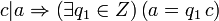 ;
;
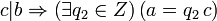 ;
;
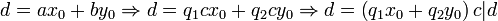 .
.
Алгоритм Евклида для целых чисел
Пусть  и
и  — целые числа, не равные одновременно нулю, и последовательность чисел
— целые числа, не равные одновременно нулю, и последовательность чисел
определена тем, что каждое 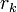 — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
— это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
Тогда НОД 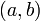 , наибольший общий делитель
, наибольший общий делитель  и
и  , равен
, равен
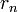 , последнему ненулевому члену этой последовательности.
, последнему ненулевому члену этой последовательности.
Существование таких 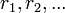 , то есть возможность деления с остатком
, то есть возможность деления с остатком  на
на  для любого целого
для любого целого  и целого
и целого 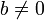 , доказывается индукцией.
, доказывается индукцией.
Корректность этого алгоритма вытекает из следующих двух утверждений:
- Пусть
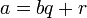 , тогда НОД
, тогда НОД 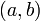 = НОД
= НОД 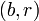 .
.
- НОД
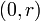 =
=  для любого ненулевого
для любого ненулевого  (так как 0 делится на любое целое число, кроме нуля).
(так как 0 делится на любое целое число, кроме нуля).
Расширенный алгоритм Евклида для целых чисел
Рассмотрим расширенный алгоритм Евклида для нахождения линейного представления наибольшего общего делителя 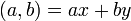 .
.
Значения 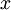 и
и 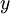 вычисляются в серии шагов, в каждом из которых мы выражаем
вычисляются в серии шагов, в каждом из которых мы выражаем 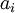 (вычисленное в процессе работы алгоритма Евклида) в форме
(вычисленное в процессе работы алгоритма Евклида) в форме 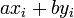 . А именно, рассмотрим последовательность
. А именно, рассмотрим последовательность
-
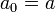 ,
, 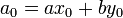 ,
,
-
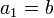 ,
, 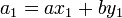 ,
,
-
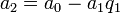 ,
, 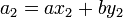 ,
,
-
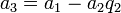 ,
, 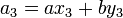 ,
,
-
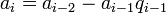 ,
, 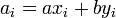 ,
,
-
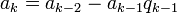 ,
, 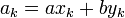 ,
,
-
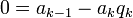 ,
, 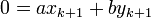 ,
,
В левом столбце алгоритма записана последовательность делений, которая получается в результате работы алгоритма Евклида и которая разрешена относительно остатков. Согласно теореме Ламе (1844 г.) число делений, которое необходимо выполнить для нахождения 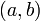 , не превосходит числа цифр в меньшем из чисел
, не превосходит числа цифр в меньшем из чисел  и
и  , умноженного на 5 (оценка наихудшего случая для алгоритма Евклида). Теорема Ламе доказывается на основе последовательности Фибоначчи.
, умноженного на 5 (оценка наихудшего случая для алгоритма Евклида). Теорема Ламе доказывается на основе последовательности Фибоначчи.
В правом столбце алгоритма каждый остаток выражен через 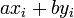 . Надо вычислить
. Надо вычислить 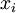 и
и 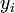 . Очевидно, что
. Очевидно, что 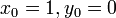 и
и 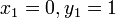 . Сравнивая обе части на i-м шаге, получим
. Сравнивая обе части на i-м шаге, получим
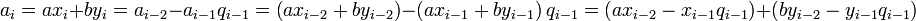 ,
,
откуда получается следующая индуктивная процедура вычисления 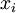 и
и 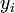 :
:
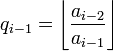 ,
,
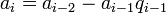 ,
,
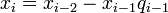 ,
,
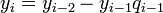 .
.
Пример (Расширенный алгоритм Евклида).
Применим расширенный алгоритм Евклида к числам 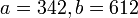 .
.
Весь алгоритм представим в виде следующей таблицы.
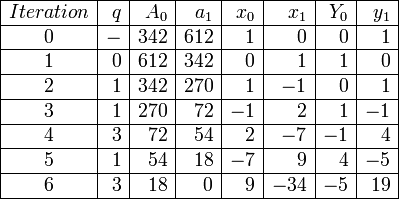
Заметим, что равенство 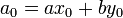 выполняется на каждом шаге итерации. Алгоритм выдаёт
выполняется на каждом шаге итерации. Алгоритм выдаёт 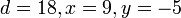 и тогда
и тогда 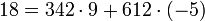 .
.