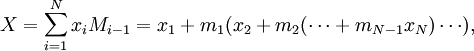Полиадический код
Содержание
Введение
Полиадический код (или система счисления со смешанным основанием от англ. associated mixed radix system (AMRS))
Любое число 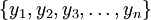 в системе остаточных классов может быть представленно в виде полиадического кода
в системе остаточных классов может быть представленно в виде полиадического кода
где
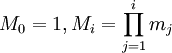 для
для 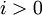 и
и 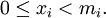
Полиадический код используется для:
- Сравнения чисел
- Перевода чисел из системы остаточных классов в обычную позиционную систему счисления
Обратное преобразование
Обратное преобразование на базе полиадического кода, базируется на идее, что любое число X может быть представлено в системе взаимно простых чисел 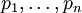 , как [1]:
, как [1]:
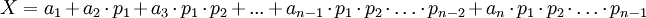 , где
, где 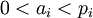
-
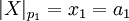
-
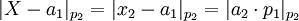 =>
=> 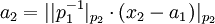
-
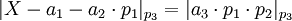 =>
=> 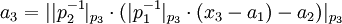
-
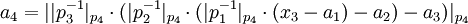
- ...
-
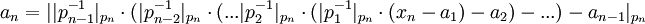
Для использования этого метода требуются константы вида 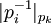 . Можно также заметить, что начинать вычисление
. Можно также заметить, что начинать вычисление 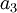 можно, как только появилось значение
можно, как только появилось значение 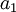 . На основе этого метода можно строить конвейерные преобразователи.
. На основе этого метода можно строить конвейерные преобразователи.
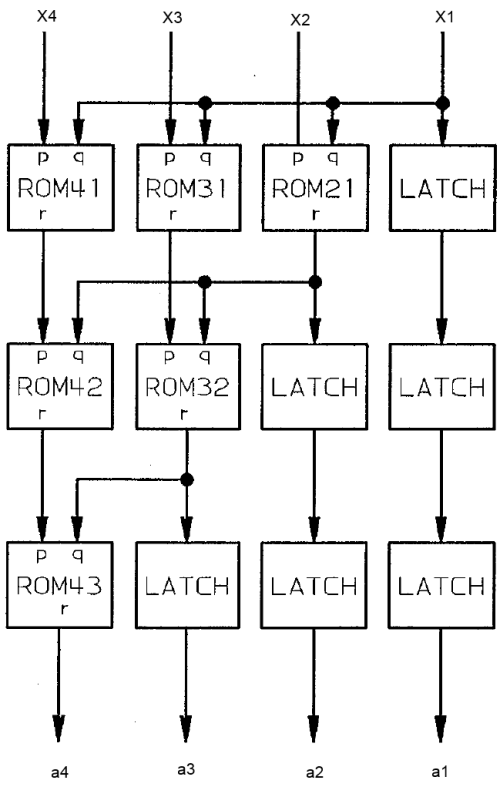
Конвейерный преобразователь в полиадический код
Используя формулы выше можно нарисовать схему конвейерного преобразователя. В данном случае мы используем модулярный базис из 4 элементов:
- ROMij - это таблица выполняющая следующее преобразование
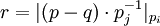 . Для больших значений модулей таблица может быть заменена на последовательный набор арифметических операций (вычитание, умножение на константу и взятие модуля)
. Для больших значений модулей таблица может быть заменена на последовательный набор арифметических операций (вычитание, умножение на константу и взятие модуля)
- LATCH - элемент памяти сохраняющий значение до следующего такта
- На преобразование модулярного представления в полиадический код требуется N-1 ступеней конвейера.
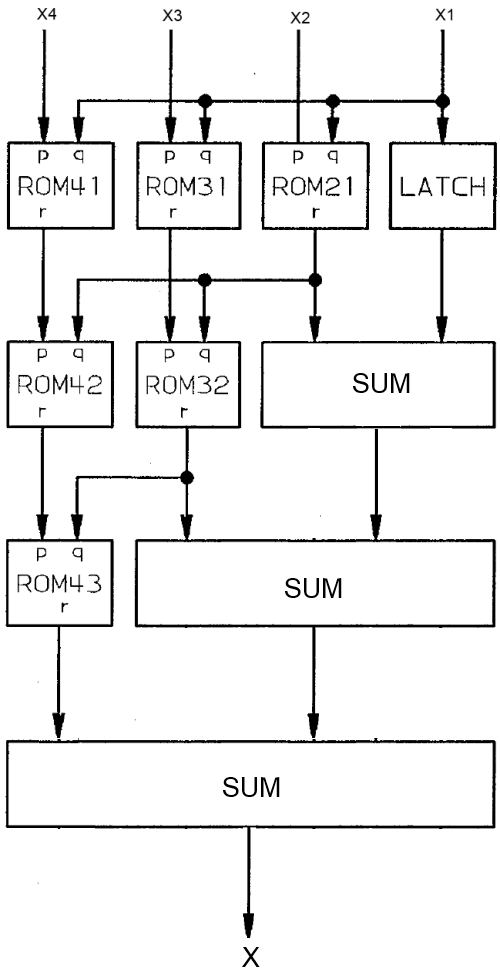
Обратный конвейерный преобразователь на базе полиадического кода
Этот преобразователь используется для восстановления числа 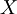 из модулярного кода, заданного набором остатков
из модулярного кода, заданного набором остатков 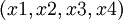 .
.
- ROMij - это таблица выполняющая следующее преобразование
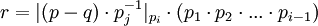 . Для больших значений модулей таблица может быть заменена на последовательный набор арифметических операций (вычитание, умножение на константу и взятие модуля)
. Для больших значений модулей таблица может быть заменена на последовательный набор арифметических операций (вычитание, умножение на константу и взятие модуля)
- LATCH - элемент памяти сохраняющий значение до следующего такта
- SUM - обычный сумматор
- На преобразование модулярного представления в позиционный вид требуется N ступеней конвейера.
- В отличие от преобразования в полиадический код, данный преобразователь получается более громоздким из-за более сложной структуры ROMij и наличия сумматоров, битовый размер которых растет в нижней части конвейера.
Коррекция ошибок на базе полиадического кода
Пусть задан набор модулей 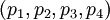 , где
, где 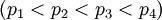 . Из них первые два
. Из них первые два 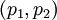 являются информационными, а последние два
являются информационными, а последние два 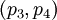 - проверочными.
- проверочными.
Ссылки
- [1] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York.
- [2] Патент "Efficient structure for computing mixed-radix projections from residue number systems"