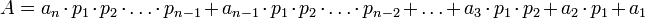Перевод числа из СОК в обобщенную позиционную систему

Рассмотрим метод определения величины числа связанный с переводом числа из системы остаточных классов в обобщенную позиционную систему (ОПС). Для этого выявим связь между представлением некоторого числа в этих двух системах.

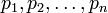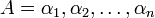Пусть СОК задается основаниями $p_1, p_2, \ldots, p_n$ и $A = {\alpha}_1, {\alpha}_2, \ldots, {\alpha}_n$ - число в этой системе. И пусть 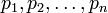$p_1, p_2, \ldots, p_n$ являются также основаниями ОПС, тогда число $A$ можно представить в виде

$A = a_n\cdot p_1\cdot p_2\cdot \ldots \cdot p_{n-1} + a_{n-1}\cdot p_1\cdot p_2\cdot \ldots \cdot p_{n-2} + \ldots + a_3\cdot p_1\cdot p_2 + a_2\cdot p_1 + a_1$

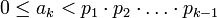где $0\le a_k<p_1\cdot p_2\cdot \ldots \cdot p_{k-1}$ – коэффициенты (цифры) ОПС.

Очевидно, что диапазоны чисел, представимых в СОК и ОПС совпадают, т.е. можно говорить о наличии взаимно однозначного соответствия между множеством представлений чисел в СОК и ОПС.

Это равенство можно переписать в следующем виде:

$A = a_1 + p_1(a_2 + p_2(a_3 + \ldots +p_{n-2}(a_{n-1} + p_{n-1} a_n) \ldots ))$,

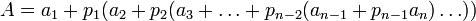откуда следует, что цифры ОПС могут быть получены из соотношений:

$a_1 = A - \left[ \frac{A}{p_1}\right] \cdot p_1 = A - A_1\cdot p_1$, где $A_1 = \left[ \frac{A}{p_1}\right]$,

$a_2 = A_1 - \left[ \frac{A_1}{p_2}\right] \cdot p_2 = A_1 - A_2\cdot p_2$, где $A_2 = \left[ \frac{A_1}{p_2}\right]$,

$\ldots$

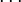
$a_n = A_{n-1} - \left[ \frac{A_{n-1}}{p_n}\right] \cdot p_n = A_{n-1} - A_n\cdot p_n$, где $A_n = \left[ \frac{A_{n-1}}{p_n}\right]$.

Причем при определении цифр 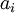$a_i$ по этим формулам все вычисления можно вести в СОК.

Действительно, из формул следует, что 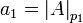$a_1 = {|A|}_{p_1}$, т.е.